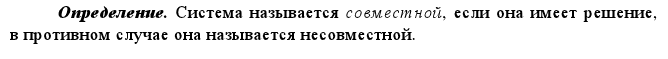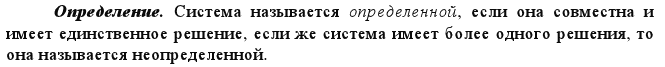Системы линейных уравнений. Совместимость. Определенность. Равносильность. Формулы Крамера решения системы линейных уравнений
Определители матриц и их свойства.
Определителем (детерминантом) 2го порядка матрицы А называется выражение (число), обозначаемое det A и определяемое равенством: произведение элементов главное диагонали - произведение элементов побочной диагонали матрицы.
Определителем 3го порядка матрицы А называется выражение (число): правило треугольника(сложение произведений главной диагонали и треугольников и вычитание произведений побочной диагонали и треугольников).
Свойства:
1) Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е. для каждой квадратной матрицы А detА = det АТ.
2) При перестановке двух строк (столбцов) определитель меняет свой знак.
3) Определитель с 2мя одинаковыми строками (столбцами) равен 0.
4) Общий множитель всех элементов какой-либо строки (столбца) можно выносить за знак определителя. Если все элементы какой-либо строки (столбца) умножить на одно и то же число К, то значение определителя изменится в К раз. Чтобы умножить определитель на число, нужно какую-либо строку (столбец) определителя умножить на это число.
5) Если все элементы какой-либо строки (столбца) равны 0, то определитель равен 0.
6) Если каждый элемент какой-нибудь строки (столбца) определителя состоит из суммы двух слагаемых, то этот определитель равен сумме двух определителей, причем в одном из них соответствующая строка (столбец) состоит из первых слагаемых, а в другом - из вторых слагаемых.
7) Определитель, у которого соответственные элементы 2х строк (столбцов) пропорциональны, равен 0.
8) Определитель не изменится от прибавления ко всем элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца.
Минором Мij элемента aij квадратной матрицы А называется определитель матрицы, полученный из матрицы А путем удаления i-той строки и j-ого столбца.
Алгебраическим дополнением Аijэлемента аij называется выражение: Аij = (-1)i+j * Mij.
Определитель n-ого порядка квадратной матрицы А равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
Определитель n-ого порядка можно разложить также по любому столбцу: det A = a1jA1j + a2jA2j + ...+ anjAnj, где j=1,2,K,..,n.
Матрицы. Линейные операции с матрицами и их свойства.
Матрицейназывается таблица, состоящая из mxn элементов некоторого множества, расположенных в m строках и n столбцах. Матрица, элементами которой являются числа, называется числовой матрицей.
Обозначение: Аmxn. Если m=n, то матрица называется квадратной, число n - ее порядок. Главная, побочная диагональ.
Операции: сложение матриц, умножение матриц на число. Две матрицы одного и того же размера называются равными, если их соответствующие элементы равны.
Суммой двух матриц А и В одного и того же размера называется матрица С, обозначаемая как С=А+В.
Свойства сумм матриц: 1) А+В=В+А 2) (А+В)+С=А+(В+С) 3) А+0=0+А=А
Произведением матрицы А на число К называется матрица В = К*А того же размера, что и матрица А, Элементы которой равны произведениям соответствующих элементов матрицы А на число К.
Свойства произведения матрицы на число: 1) если К=0, то получаем нуль матрицу 0*А=0 2) если К=1, то 1*А=А 3) К*(А+В)=К*А + К*В 4) С*(К*А)=(С*К)*А=К*(С*А) 5) (С+К)*А=С*А+К*А 6) А-В=А+(-1)*В
Произведением матрицы А на В называется матрица С=А*В, у которой число строк К равно числу строк матрицы А, а число столбцов M равно числу столбцов матрицы В.
Свойства произведений матриц: 1) К(АВ)=КА(В)=А(КВ) 2) А(ВС)=(АВ)С 3) А(В+С)=АВ+АС 4) (А+В)С=АС+ВС
Обратная матрица. Определение. Формулы для нахождения ее элементов.

Системы линейных уравнений. Совместимость. Определенность. Равносильность. Формулы Крамера решения системы линейных уравнений.