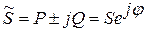Комплексные числа и математические действия с ними

		+1

A

α

a

b

Формы представления комплексного числа:

1. Алгебраическая форма записи:

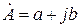
а – действительная часть комплексного числа;

jb – мнимая часть комплексного числа;

j – мнимая единица

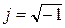
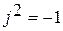
2. Показательная форма записи комплексного числа:

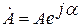
A – модуль комплексного числа;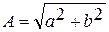

α – аргумент комплексного числа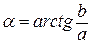

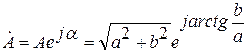
3. Тригонометрическая форма записи комплексного числа:

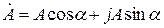
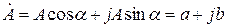
Примеры:

1. Представить комплексные числа в показательной форме записи:

· A = 3 – j4

· A = 5+ j5

· A = - 5+ j5

· A = -5 - j5

2. Представить комплексные числа в алгебраической форме записи:

·

·

·

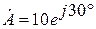
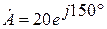
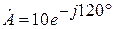
Математические действия.

Сложение (выполняется только в алгебраической форме записи)

· Ȧ₁ = 3 – j4

· Ȧ2 = - 6 + j9

Вычитание (выполняется только в алгебраической форме записи)

· Ȧ₁ = 3 – j4

· Ȧ₂ = - 6 + j9

Выполнить: Ȧ₁ - Ȧ₂

Ȧ₂ - Ȧ₁

Умножение (выполняется в алгебраической и показательной форме записи)

· Ȧ₁ = 3 – j4

· Ȧ₂ = - 6 + j9

Выполнить: Ȧ₁∙ Ȧ₂

·

·

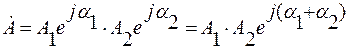
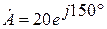
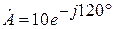
Выполнить: Ȧ₁∙ Ȧ₂

Деление (выполняется в алгебраической и показательной форме записи)

При делении в алгебраической форме записи необходимо домножить числитель и знаменатель на сопряженный комплекс знаменателя.

Сопряженное комплексное число имеет противоположный знак перед j.

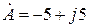
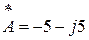
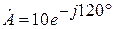
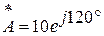
· Ȧ₁ = 3 – j4

· Ȧ₂ = - 6 + j9

Выполнить: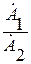

·

·

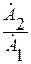
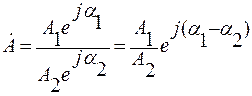
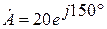
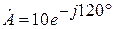
Выполнить: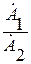

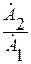
Выражение основных электрических величин с помощью комплексных чисел.

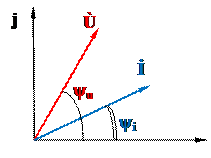
ЭДС, напряжение, сила тока

Если ЭДС, напряжение или ток изменяются по синусоидальным законам
u = U_m sin (ωt + ψ_u), i = I_m sin (ωt + ψ_i), то их можно изобразить в виде векторов на комплексной плоскости и записать в виде комплексов действующих значений:

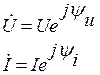
Примеры:

1. Представить синусоидальный ток i = 0,141 sin (ωt - 60°) A в виде комплекса действующего значения.

2. Записать выражение для мгновенного значения синусоидальной ЭДС, если задан комплекс её действующего значения 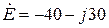В.

Сопротивления

В алгебраической форме записи активное сопротивление в комплексном виде представляется действительным числом, реактивное сопротивление – мнимым числом (индуктивное сопротивление - положительным, емкостное отрицательным).

В показательной форме записи модуль комплексного числа соответствует численному значению сопротивления, аргумент – углу сдвига фаз, создаваемому этим сопротивлением.

R =R = Re^j0°

X_L = jX_L = X_Le^j90°

X_C = -jX_C=X_Ce^-j90°

Z =R ±jX = Ze^jφ

Проводимости

В алгебраической форме записи активная проводимость в комплексном виде представляется действительным числом, реактивная проводимость – мнимым числом (индуктивная проводимость - отрицательным, емкостная - положительным).

В показательной форме записи модуль комплексного числа соответствует численному значению проводимости, аргумент – углу сдвига фаз, взятому с обратным знаком.

G=g = ge^j0°

B_L = - jb_L = b_Le^-j90°

B_C = jb_C=b_Ce^j90°

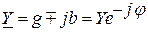
Мощности

Полная мощность в комплексном виде определяется как произведение комплекса действующего значения напряжения и сопряженного комплекса тока:

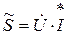
Запись в комплексном виде: