Производная сложной функции
В п. 5.2 был рассмотрен вопрос о вычислении частных производных функции нескольких переменных, когда ее аргументами являются независимые переменные. Однако довольно часто встречаются случаи, когда аргументы функции нескольких переменных в свою очередь зависят от других переменных. Это так называемые сложные функции, с которыми мы уже сталкивались при изучении дифференцирования функций одной переменной. Рассмотрим три случая.
1. Пусть дана функция двух переменных 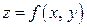 с областью определения
с областью определения 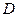 . При этом аргументы функции
. При этом аргументы функции 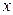 и
и 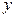 , в свою очередь, зависят от одной переменной
, в свою очередь, зависят от одной переменной 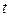 . Переменная
. Переменная 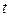 меняется таким образом, что
меняется таким образом, что 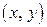 не выходят из области определения функции.
не выходят из области определения функции.
В принципе, подставляя выражения 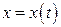 и
и 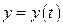 в функцию
в функцию 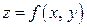 , можно свести ее к функции одной переменной:
, можно свести ее к функции одной переменной: 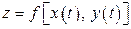 . Значит, в конечном счете,
. Значит, в конечном счете, 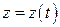 и может быть продифференцирована по этой переменной. Выясним, каким образом можно вычислить
и может быть продифференцирована по этой переменной. Выясним, каким образом можно вычислить 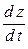 без подстановки
без подстановки 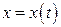 и
и 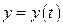 в функцию
в функцию 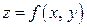 .
.
Пусть все частные производные 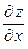 и
и 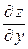 , а также производные
, а также производные 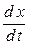 и
и 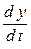 определены и непрерывны для всех возможных значений
определены и непрерывны для всех возможных значений 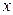 ,
, 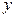 и
и 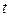 . Возьмем некоторое конкретное значение независимой переменной
. Возьмем некоторое конкретное значение независимой переменной 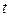 и дадим ей приращение
и дадим ей приращение 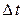 :
: 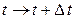 . Это приведет к тому, что приращения получат обе переменные
. Это приведет к тому, что приращения получат обе переменные 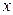 и
и 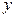 :
: 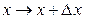 ,
, 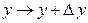 . Но в этом случае должна измениться и сама функция
. Но в этом случае должна измениться и сама функция 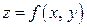 , причем, как показано в п. 5.3, она получит полное приращение
, причем, как показано в п. 5.3, она получит полное приращение
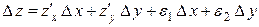 .
.
Разделим обе части полученного равенства на 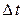 и перейдем к пределу при
и перейдем к пределу при 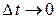 , то есть найдем
, то есть найдем 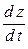 :
:
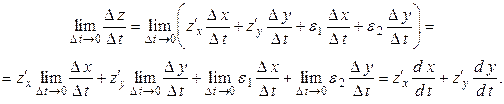
Окончательно данное выражение можно записать следующим образом:
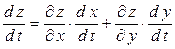 .
.
Если 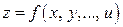 , где
, где 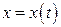 ,
, 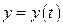 ,…,
,…, 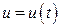 , то:
, то:
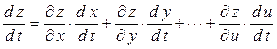 .
.
2. Рассмотрим теперь функцию 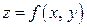 при условии, что
при условии, что 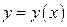 . При подстановке
. При подстановке 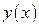 в
в 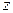 получаем функцию, зависящую только от одной переменной:
получаем функцию, зависящую только от одной переменной: 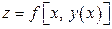 . Следовательно, в данном случае можно вычислить
. Следовательно, в данном случае можно вычислить 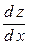 .
.
Если производные 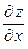 ,
, 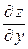 ,
, 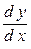 непрерывны в области определения функции, то данный случай можно привести к предыдущему. Действительно, положив
непрерывны в области определения функции, то данный случай можно привести к предыдущему. Действительно, положив 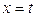 , получаем
, получаем 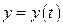 и
и 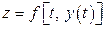 . Таким образом,
. Таким образом,
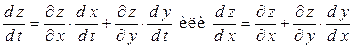 .
.
В полученном выражении имеются две производные по 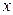 . Одна из них
. Одна из них 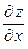 – частная производная функции двух переменных, для ее вычисления необходимо считать
– частная производная функции двух переменных, для ее вычисления необходимо считать 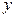 константой. Другая производная
константой. Другая производная 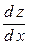 – это производная сложной функции одной переменной
– это производная сложной функции одной переменной 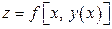 . Эта производная, в отличие от первой, называется полной производной по
. Эта производная, в отличие от первой, называется полной производной по 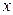 .
.
Если 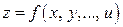 , где
, где 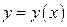 ,…,
,…, 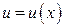 , то
, то
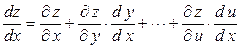 .
.
3. Рассмотрим теперь наиболее общий случай: где 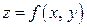 и при этом
и при этом 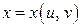 ,
, 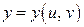 .. Очевидно, подставляя
.. Очевидно, подставляя 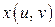 и
и 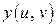 в
в 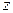 , мы снова получим функцию двух переменных
, мы снова получим функцию двух переменных 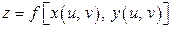 . Для этой функции можно вычислить частные производные
. Для этой функции можно вычислить частные производные 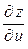 и
и 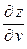 .
.
Пусть снова 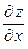 ,
, 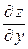 ,
, 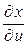 ,
, 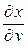 ,
, 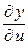 ,
, 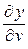 непрерывны в области определения функции
непрерывны в области определения функции 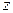 . Найдем вначале
. Найдем вначале 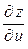 . При этом, очевидно, необходимо считать
. При этом, очевидно, необходимо считать 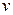 константой. Но тогда
константой. Но тогда 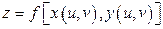 будет функцией только одной переменной
будет функцией только одной переменной 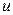 и можно воспользоваться выражением, полученным в случае 1:
и можно воспользоваться выражением, полученным в случае 1:
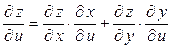 .
.
Аналогично
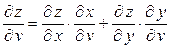 .
.
