Производные неявной, параметрической функций

Найти производные от функций y, заданных неявно:

364. y²cos x = a²sin 3x. 365. y = 1 + xe ^y.

366. 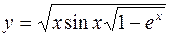. 367. y = (x² + 1)^{sin x}. 368. .

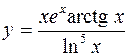369. На параболе y = x² взяты две точки с абсциссами x₁ = 1, x₂ = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей?

370. Провести нормаль к линии y = x·ln x параллельно прямой 2x –2y +3 = 0.

Найти производные от функции y по x:

371. 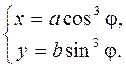372.

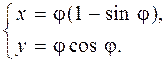
Найти производные от функций y, заданных неявно:

373. sin (xy) + cos (xy) = tg (x + y). 374. ysin x – cos (x – y) = 0.

375. 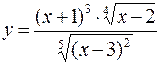. 376. 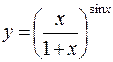. 377. .

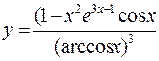378. Составить уравнения касательной и нормали к линии 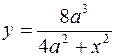в точке с абсциссой x = 2a.

379. Провести касательную к гиперболе 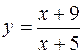так, чтобы она прошла через начало координат.

Найти производные от функции y по x:

380. 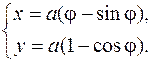381.

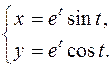
Дифференциал функции. Производные высших порядков

382. Найти дифференциал функции: 1) 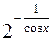; 2) .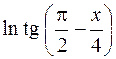

383. Вычислить приближенно .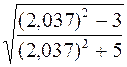

384. Выразить дифференциал сложной функции через независимую переменную и ее дифференциал:

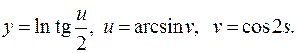
385. f (x) = (x + 10)⁶; 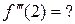386. f (x) = e^{2x -1};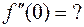

387. Найти вторую производную от функции у = (1 + х²)arctg x.

388. 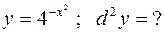389.

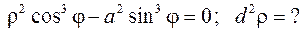
390. Найти дифференциал функции:

1) 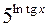; 2) .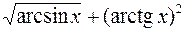

391. 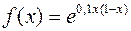. Подсчитать приближенно f (1,05).

392. Выразить дифференциал сложной функции через независимую переменную и ее дифференциал:

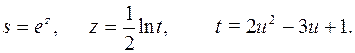
393. f (x) = x⁶ - 4x³ - 4 ; 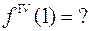394. f (x) = arctg x ;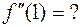

395. Найти вторую производную от функции .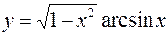

396. 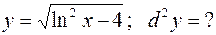397.

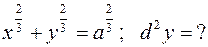
Правило Лопиталя

Пользуясь правилом Лопиталя найти пределы:

398. 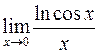. 399. 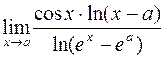. 400. .

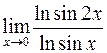401. 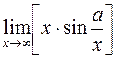. 402. 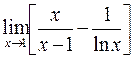. 403. .

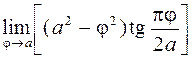404. 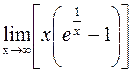. 405. 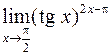. 406. .

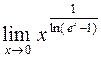407. 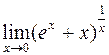. 408. 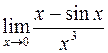. 409. .

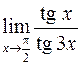410. 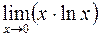. 411. 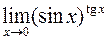. 412. .

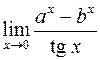413. 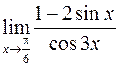. 414. 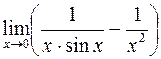. 415. .

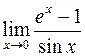416. 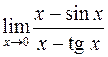. 417. 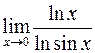. 418. .

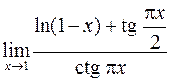419. 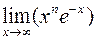. 420. 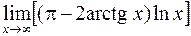. 421. .

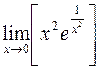422. 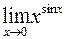. 423. 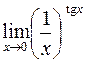. 424. 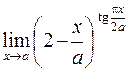. 425. .

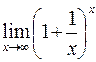426. 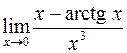. 427. 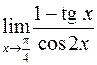. 428. .

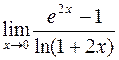429. 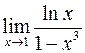. 430. 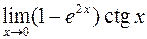. 431. .

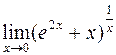Наибольшее и наименьшее значения функции

Найти наибольшее и наименьшее значения функций в указанных промежутках:

432. 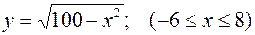. 433. .

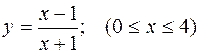434. .

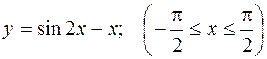435. Через данную точку P(1; 4) провести прямую так, чтобы сумма длин положительных отрезков, отсекаемых ею на координатных осях, была наименьшей.

436. Полоса железа шириной a должна быть согнута в виде открытого цилиндрического желоба (сечение желоба имеет форму дуги кругового сегмента). Найти значение центрального угла, опирающегося на эту дугу, при котором вместимость желоба будет наибольшей.

Найти наибольшее и наименьшее значения функций в указанных промежутках:

437. 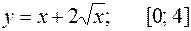. 438. .

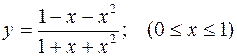439. .

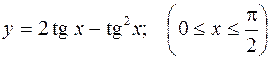440. На эллипсе 2x² + y² = 18 даны две точки A(1; 4) и B(3; 0). Найти на данном эллипсе третью точку C такую, чтобы площадь треугольника ABC была бы наибольшей.

441. Лампа висит над центром круглого стола радиуса R. При какой высоте лампы над столом освещенность предмета, лежащего на краю стола, будет наилучшая? (Освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света.)

Исследование функций на экстремум

Исследовать функции на экстремум по первой производной:

442. 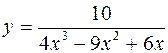. 443. 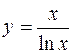. 444. .

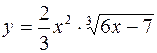Исследовать функции на экстремум по второй производной:

445. .

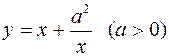Исследовать функции на экстремум по первой производной:

446. 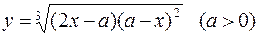. 447. .

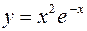448. 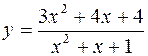. 449. .

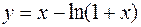Исследовать функции на экстремум по второй производной:

450. .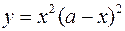