Нормальное уравнение прямой на плоскости
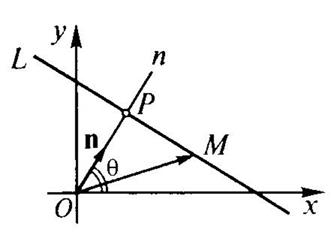 Рассмотрим произвольную прямую. Восстановим из начала координат
Рассмотрим произвольную прямую. Восстановим из начала координат 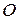 вектор нормали
вектор нормали 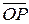 к данной прямой и единичный вектор
к данной прямой и единичный вектор 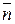 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 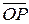 . Пусть
. Пусть 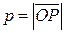 (если прямая проходит через начало координат, то
(если прямая проходит через начало координат, то 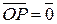 ). Пусть
). Пусть 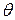 - угол между вектором
- угол между вектором 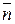 и осью абсцисс (в случае, когда
и осью абсцисс (в случае, когда 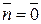 в качестве
в качестве 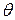 можно взять любое значение). Так как
можно взять любое значение). Так как 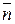 - единичный вектор, то его координаты, равные его проекциям на координатные оси, имеют вид:
- единичный вектор, то его координаты, равные его проекциям на координатные оси, имеют вид:
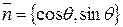 .
.
Очевидно, что точка 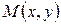 лежит на данной прямой тогда и только тогда, когда проекция вектора
лежит на данной прямой тогда и только тогда, когда проекция вектора 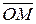 на ось, определяемую вектором
на ось, определяемую вектором 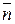 , равна
, равна 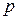 . Так как
. Так как 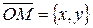 , то получаем
, то получаем
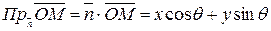 .
.
Следовательно, уравнение прямой может быть записано в виде:
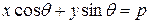
или
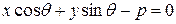 .
.
Такое уравнение называется нормальным уравнением прямой.
Рассмотрим произвольную точку  . Пусть
. Пусть 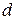 - расстояние от этой точки до прямой
- расстояние от этой точки до прямой 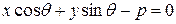 . Отклонением
. Отклонением 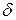 точки
точки  от этой прямой называется расстояние
от этой прямой называется расстояние 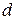 , взятое со знаком плюс, если эта точка и начало координат лежат по разные стороны от данной прямой, и взятое со знаком минус, если эта точка и начало координат лежат по одну сторону от прямой.
, взятое со знаком плюс, если эта точка и начало координат лежат по разные стороны от данной прямой, и взятое со знаком минус, если эта точка и начало координат лежат по одну сторону от прямой.
Выясним геометрический смысл левой части нормального уравнения. Спроектируем произвольную точку 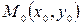 на ось, определяемую вектором
на ось, определяемую вектором 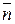 . Пусть
. Пусть 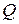 - полученная проекция, а
- полученная проекция, а 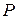 - точка пересечения прямой
- точка пересечения прямой 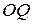 с данной прямой. Очевидно, что отклонение точки
с данной прямой. Очевидно, что отклонение точки 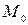 от данной прямой равно величине вектора
от данной прямой равно величине вектора 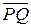 . Соответственно получаем:
. Соответственно получаем:
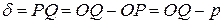 .
.
Кроме того,
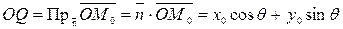 .
.
Следовательно,
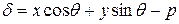 .
.
Таким образом, получаем правило: для нахождения отклонения точки от данной прямой следует в левую часть нормального уравнения этой прямой подставить координаты этой точки.
Выясним, как из общего уравнения получить нормальное уравнение. Пусть дано уравнение
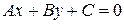 .
.
Найдем множитель 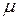 , при умножении на который общее уравнение превратится в нормальное. При этом должно выполняться:
, при умножении на который общее уравнение превратится в нормальное. При этом должно выполняться:
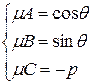 .
.
Возводя в квадрат первые два равенства и затем, складывая их, получим
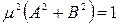 ,
,
откуда
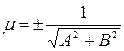 .
.
Так как расстояние 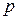 всегда неотрицательно, то из третьего равенства системы заключаем, что знак
всегда неотрицательно, то из третьего равенства системы заключаем, что знак 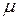 должен быть противоположен знаку
должен быть противоположен знаку 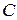 . Итак, для приведения общего уравнения к нормальному виду следует умножить его на нормирующий множитель, определяемый равенством
. Итак, для приведения общего уравнения к нормальному виду следует умножить его на нормирующий множитель, определяемый равенством 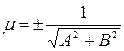 , при этом знак в последней формуле выбирается противоположным знаку коэффициента
, при этом знак в последней формуле выбирается противоположным знаку коэффициента 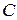 . В соответствии с этим получаем формулу для нахождения расстояния от точки
. В соответствии с этим получаем формулу для нахождения расстояния от точки 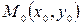 до прямой
до прямой 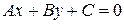 :
:
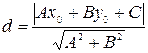 .
.
Пример.Написать уравнение прямой, проходящей через точки 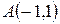 и
и 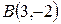 . Привести это уравнение к нормальному виду и выяснить пересекает ли эта прямая отрезок, соединяющий точки
. Привести это уравнение к нормальному виду и выяснить пересекает ли эта прямая отрезок, соединяющий точки 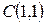 и
и 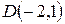 .
.
∆ Воспользуемся каноническим уравнением прямой, проходящей через заданные две точки:
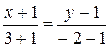
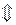
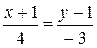 .
.
Умножив на число 12 обе части полученного уравнения, получим общее уравнение:
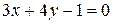 .
.
Для приведения его к нормальному виду найдем нормирующий множитель, выбрав его знак, противоположный знаку коэффициента 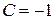 :
:
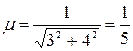 .
.
Умножив на этот множитель, получим нормальное уравнение рассматриваемой прямой:
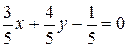 .
.
Чтобы выяснить, пересекает ли эта прямая отрезок, соединяющий точки 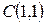 и
и 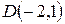 , найдем отклонения этих точек относительно этой прямой, подставив их координаты в левую часть нормального уравнения:
, найдем отклонения этих точек относительно этой прямой, подставив их координаты в левую часть нормального уравнения:
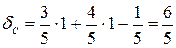 ,
,
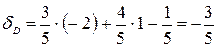 .
.
Так как отклонения точек 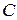 и
и 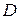 имеют противоположные знаки, то они лежат по разные стороны относительно данной прямой. Таким образом, эта прямая пересекает отрезок, соединяющий указанные точки. ▲
имеют противоположные знаки, то они лежат по разные стороны относительно данной прямой. Таким образом, эта прямая пересекает отрезок, соединяющий указанные точки. ▲
