Закрепление материала. Тест 10.1
Решение уравнений с неизвестным в знаменателе
Цели урока:
· рассмотреть различные способы решения дробных рациональных уравнений;
· обучить решению дробных рациональных уравнений по алгоритму;
· проверка уровня усвоения темы путем проведения тестовой работы.
· развитие умения правильно оперировать полученными знаниями, логически мыслить;
· воспитание самостоятельности при решении учебных задач;
Ход урока
Организационный момент.
Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока
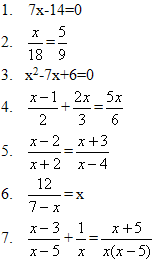2. Актуализация знаний. Фронтальный опрос, устная работа с классом.
А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:
1. Что такое уравнение? (Равенство с переменной или переменными.)
2. Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа - в правую. Привести подобные слагаемые.).
3. Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений.
4. Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
5. Какие свойства используются при решении уравнений?
6. Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)
Повторение материала.
- Решить в тетрадях и на доске уравнение №2.
Решение: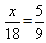 
; 9х = 18∙5; 9х = 90; х = 90:9; х = 10; Ответ: 10.
- Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).
- Решить в тетрадях и на доске уравнение №4.
- Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).
Теперь попытайтесь решить уравнение №7 одним из способов.
Решение:
| 1 способ: | 2 способ: | ||
| (х2-2х-5)х(х-5)=х(х-5)(х+5) |  | ||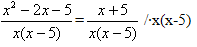
| (х2-2х-5)х(х-5)-х(х-5)(х+5)=0 | х2-2х-5=х+5 | ||
| х(х-5)(х2-2х-5-(х+5))=0 | х2-2х-5-х-5=0 | ||
| х(х-5)(х2-3х-10)=0 | х2-3х-10=0 | ||
| х=0 х-5=0 х2-3х-10=0 | D=49 | ||
| х1=0 х2=5 D=49 | |||
| х3=5 х4=-2 | х3=5 х4=-2 | ||
| Ответ: 0;5;-2. | Ответ: 5;-2. |
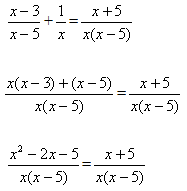
Объясните, почему так получилось? Почему в одном случае три корня, в другом – два? Какие же числа являются корнями данного дробно-рационального уравнения?
До сих пор учащиеся с понятием посторонний корень не встречались, им действительно очень трудно понять, почему так получилось. Если в классе никто не может дать четкого объяснения этой ситуации, тогда учитель задает наводящие вопросы.
· Чем отличаются уравнения № 2 и 4 от уравнений № 5,6,7? (В уравнениях № 2 и 4 в знаменателе числа, № 5-7 – выражения с переменной.)
· Что такое корень уравнения? (Значение переменной, при котором уравнение обращается в верное равенство.)
· Как выяснить является ли число корнем уравнения? (Сделать проверку.)
Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данным способом. Дети сами формулируют алгоритм.
Алгоритм решения дробных рациональных уравнений:
1. Перенести все в левую часть.
2. Привести дроби к общему знаменателю.
3. Составить систему: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
4. Решить уравнение.
5. Проверить неравенство, чтобы исключить посторонние корни.
6. Записать ответ.
Обсуждение: как оформить решение, если используется основное свойство пропорции и умножение обеих частей уравнения на общий знаменатель. (Дополнить решение: исключить из его корней те, которые обращают в нуль общий знаменатель).
Закрепление материала. Тест 10.1