Единственность предела. Ограниченные функции
Сложная функция
Определение сложной функции.Дана функция  , причём аргумент
, причём аргумент  является функцией от
является функцией от 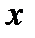 , т. е.
, т. е.  . Область значений функции
. Область значений функции  является частью области определения функции
является частью области определения функции  . Следовательно, каждому
. Следовательно, каждому 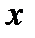 из области определения
из области определения  отвечает определённое значение
отвечает определённое значение  , а этому значению
, а этому значению  отвечает определённое значение
отвечает определённое значение  . Таким образом, каждому указанному
. Таким образом, каждому указанному 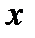 отвечает определённое значение
отвечает определённое значение  . Это означает, что
. Это означает, что  есть функция от
есть функция от 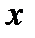 . Она называется сложной функцией от
. Она называется сложной функцией от 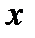 и записывается в виде
и записывается в виде  , где
, где  – внутренняя функция,
– внутренняя функция,  – внешняя функция,
– внешняя функция,  – промежуточный аргумент. Например, пусть
– промежуточный аргумент. Например, пусть  где
где  , тогда получим сложную функцию
, тогда получим сложную функцию  .
.
Предел функции.
1.Пусть 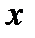 – переменная величина, которая принимает положительные значения и неограниченно увеличивается. В этом случае будем говорить, что
– переменная величина, которая принимает положительные значения и неограниченно увеличивается. В этом случае будем говорить, что 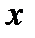 стремится к плюс бесконечности и писать
стремится к плюс бесконечности и писать  . Пусть при этом заданная функция
. Пусть при этом заданная функция  принимает значения, всё более и более близкие к некоторому числу
принимает значения, всё более и более близкие к некоторому числу 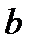 , в том смысле, что величина
, в том смысле, что величина  уменьшается и приближается к нулю. В этом случае будем говорить, что число
уменьшается и приближается к нулю. В этом случае будем говорить, что число 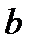 есть предел функции
есть предел функции  при
при  .
.
Определение. Число 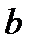 называется пределом функции
называется пределом функции  при
при  , если для любого положительного числа
, если для любого положительного числа  каким бы малым оно ни было, найдётся такое положительное число
каким бы малым оно ни было, найдётся такое положительное число  что для всех
что для всех  выполняется неравенство
выполняется неравенство  т. е. символически
т. е. символически  В этом случае будем писать
В этом случае будем писать 
2. Пусть переменная 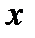 принимает отрицательные значения, и абсолютная величина
принимает отрицательные значения, и абсолютная величина  возрастает. В этом случае говорят, что
возрастает. В этом случае говорят, что  . Дадим определение предела функции
. Дадим определение предела функции  при
при  символически. Число
символически. Число 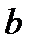 называется пределом функции
называется пределом функции  при
при  , если
, если  В этом случае пишут
В этом случае пишут  .
.
3. Пусть 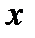 изменяется, принимая как положительные, так и отрицательные значения, абсолютная величина
изменяется, принимая как положительные, так и отрицательные значения, абсолютная величина  неограниченно увеличивается. Тогда говорят, что
неограниченно увеличивается. Тогда говорят, что  стремится к бесконечности, и пишут
стремится к бесконечности, и пишут  . Число
. Число  называется пределом функции
называется пределом функции  при
при  , если для любого положительного
, если для любого положительного  найдётся такое число
найдётся такое число  , что для всех
, что для всех 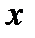 , абсолютная величина которых
, абсолютная величина которых  , имеет место неравенство
, имеет место неравенство  т. е.
т. е.

В этом случае пишут  .
.
4. Пусть 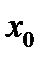 – заданное число. Рассмотрим предел функции
– заданное число. Рассмотрим предел функции  , когда
, когда  и
и  . Число
. Число 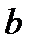 называется пределом слева функции
называется пределом слева функции  при
при  , если для любого числа
, если для любого числа  найдётся такое число
найдётся такое число  что для всех точек интервала
что для всех точек интервала  выполняется неравенство
выполняется неравенство  , каким бы малым
, каким бы малым  ни было. Сказанное можно записать символически в виде
ни было. Сказанное можно записать символически в виде

В этом случае пишут  .
.
По аналогии дадим определение предела функции  справа при
справа при  . Число
. Число 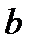 называется пределом функции
называется пределом функции  при
при  справа, если
справа, если

В этом случае пишут  .
.
5. Число 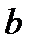 называется (двусторонним) пределом функции
называется (двусторонним) пределом функции  при
при  , если для любого числа
, если для любого числа  , каким бы малым оно ни было, найдётся такое число
, каким бы малым оно ни было, найдётся такое число  что для всех точек интервала
что для всех точек интервала  отличных от
отличных от 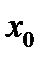 , выполняется неравенство
, выполняется неравенство  , т. е.
, т. е.

В этом случае пишут  .
.
Единственность предела. Ограниченные функции.
Теорема 1. Если функция имеет предел при  , то этот предел будет единственным.
, то этот предел будет единственным.
Доказательство. Дано, что функция  при
при  имеет предел
имеет предел  . Докажем, что никакое другое число, например,
. Докажем, что никакое другое число, например,  , не может быть пределом этой функции при
, не может быть пределом этой функции при  .
.
Возьмём  таким малым, чтобы было
таким малым, чтобы было  . Так как
. Так как 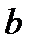 – предел функции
– предел функции 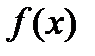 при
при  , то для выбранного нами числа
, то для выбранного нами числа  найдётся такое число
найдётся такое число  , что для всех
, что для всех  значения функции
значения функции 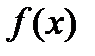 будут удовлетворять неравенству (1), следовательно, и (2). Поэтому для всех
будут удовлетворять неравенству (1), следовательно, и (2). Поэтому для всех  имеем
имеем
 . (3)
. (3)
Предположим, что  . Тогда для выбранного выше числа
. Тогда для выбранного выше числа  найдётся такое число
найдётся такое число  , что для всех
, что для всех  будет выполняться неравенство
будет выполняться неравенство  . Следовательно, для всех
. Следовательно, для всех  будем иметь
будем иметь
 . (4)
. (4)
Пусть  – наибольшее из чисел
– наибольшее из чисел  . Тогда для всех
. Тогда для всех  выполняются оба неравенства (3), (4). Из них получим, что
выполняются оба неравенства (3), (4). Из них получим, что  . Но это противоречит условию, что
. Но это противоречит условию, что  , поэтому сделанное предположение должно быть отброшено.
, поэтому сделанное предположение должно быть отброшено.
Функция называется ограниченной на некотором множестве  значений
значений 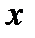 , если существует такое положительное число
, если существует такое положительное число  , что для всех
, что для всех 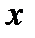 из множества
из множества  выполняется неравенство
выполняется неравенство  .
.
Теорема 2. Если функция  при
при 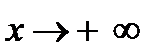 имеет предел, то эта функция является ограниченной на некотором бесконечном интервале
имеет предел, то эта функция является ограниченной на некотором бесконечном интервале  .
.
Доказательство. Дано, что  . Для числа
. Для числа  (как и для любого
(как и для любого  ) найдётся такое число
) найдётся такое число 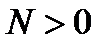 , что для всех
, что для всех 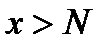 будет выполняться неравенство
будет выполняться неравенство  . Согласно свойству абсолютной величины
. Согласно свойству абсолютной величины  . Поэтому для всех
. Поэтому для всех  имеет место
имеет место  . Итак, для
. Итак, для 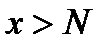 имеем
имеем  , следовательно, для всех
, следовательно, для всех 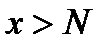 будем иметь
будем иметь  . Это означает, что функция
. Это означает, что функция 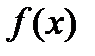 ограничена в интервале
ограничена в интервале  . Теорема доказана.
. Теорема доказана.
Теорема 3. Если при 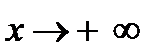 функция
функция 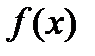 имеет отличный от нуля предел
имеет отличный от нуля предел  , то функция
, то функция  ограничена на некотором бесконечном интервале
ограничена на некотором бесконечном интервале  .
.
Теорема доказывается аналогично предыдущей.
