Определение ускорений точек тела плоской фигуры

3.6.1. Метод полюса

Поскольку движение плоской фигуры можно разложить на поступательное движение полюса точки А, при котором все точки фигуры движутся с ускорением , и вращательное движение вокруг этого полюса, тогда ускорение точки В плоской фигуры определим согласно уравнению (рис.26)

, (73)

где – ускорение полюса;

– ускорение вращательного движения точки В вокруг полюса точки А;

В свою очередь вектор ускорения можно представить как векторную сумму векторов

, (74)

где – касательное (вращательное) ускорение вращательного движения точки В вокруг полюса точки А;

– нормальное (центростремительное) ускорение вращательного движения точки В вокруг полюса точки А.

Вектор направляется из точки В перпендикулярно ВА ( ^ВА ) в сторону вращения углового ускорения (см. рис.26); численно равен

. (75)

Вектор направляется вдоль линии ВА из точки В к полюсу – точке А ( //ВА ); численно равен

. (76)

Полное ускорение по модулю определим по теореме Пифагора, поскольку вектора и взаимно перпендикулярны

(77)

Рис.26.

Ускорение точки В ( ) из уравнения (73) может быть найдено геометрически, с помощью построения многоугольника ускорений в соответствующем масштабе либо аналитическим путем проецирования ускорений в выражении (73) на выбранные координатные оси.

3.6.2. Метод мгновенного центра ускорений (МЦУ)

При движении плоской фигуры в каждый момент времени существует такая точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений данной фигуры.

Рис.27. Рис.28. Рис.29.

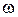Для нахождения МЦУ требуется знать: ускорение некоторой точки А данной фигуры ( ), угловую скорость ( ) и угловое ускорение ( 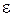) движения фигуры (рис.27).

Последовательность нахождения положение МЦУ:

– определим значение угла aкоторый образуется между вектором и отрезком ВА (см. рис.26),

; (78)

– от точки А под углом aк вектору ускорения точки А ( ) в сторону углового ускорения фигуры (e) проводим прямую АС (см. рис.27);

– на линии АС откладываем отрезок AQ

. (79)

Построенная таким образом точка Qбудет мгновенным центром ускорений (МЦУ) данной плоской фигуры. Ускорение всех других точек данной фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра ускорений Q.

Определим ускорение произвольной точки В плоской фигуры, зная положение МЦУ, точки Qданной фигуры (рис.28).

Численное значение вектора ускорения точки В составит

(80)

Для направления вектора ускорения точки В требуется от отрезка QВ отложить угол (в том же направлении, что и от отрезка АQ), вектор будет направлен из точки В (рис.29).

Практическая работа 2