Расчет переходных процессов
Пример 9. Рассчитать изменение тока i1 и напряжения u2 в схеме четырехполюсника (рис. 16, а) для режима холостого хода (Zн = ) на интервале t0 t t0 + T при подключении его к клеммам с напряжением u12 в момент t0, когда напряжение u11(t0) = 0, du11(t0)/dt > 0, т.е. в момент перехода отрицательной полуволны напряжения в положительную (рис. 16, б). Значения параметров элементов схемы и входного напряжения: R1 = 45 Ом, R2 = 8 Ом,
R3 = 10 Ом, L = 50 мГн, С = 250 мкФ, u11(t) = 14,1sin(103t + p/4) B, u12(t) = [20, t0+ t t0 + T/2– ; –20, t0 + T/2+ t t0+ T–], T = 6,28 10–3 с.
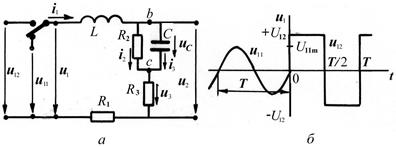
Рис. 16
Решение. Подготовим схему — выберем условно положительные направления токов и напряжений. Определим независимые начальные условия uC (t0+) и iL(t0+) из значений uC (t) и iL(t), рассчитанных до коммутации: uC (t0+) = uC (t0–), iL(t0+) = iL(t0–). Значение uC (t) и iL(t) = i1(t) рассчитаем с использованием метода комплексных амплитуд: I1m = U1m / Zвх, U1m = 14,1e jp/4, Zвх = R1 + jwL1 + R3 + R2(–j / wC) / (R2 – j / wC) = =45 + j50 + 10 + 8(–j4) / (8 – j4) = 56,6 + j46,8. Тогда I1m = (10 + j10)/(56,6 + j46,8) = (0,1917 + j0,0182) = =0,193exp( j5,42)  i1(t) = 0,193sin(103t + 5,42). Напряжение UCm = Zbc I1m = [R2(–j / wC) / (R2 – j / wC)] I1m = =(1,6 – j3,2) (0,1917 + j0,0182) = 0,365 – j0,584 = 0,689exp(–j58)
i1(t) = 0,193sin(103t + 5,42). Напряжение UCm = Zbc I1m = [R2(–j / wC) / (R2 – j / wC)] I1m = =(1,6 – j3,2) (0,1917 + j0,0182) = 0,365 – j0,584 = 0,689exp(–j58) 
 uC (t) = 0,689sin(103t – 58).
uC (t) = 0,689sin(103t – 58).
Определим время коммутации t0 из заданного условия u11(t0) = 0, du11(t0) / dt > 0: u11(t0) = 14,1sin(wt0 + p/4) = 0, отсюда t0 = –p/(4w), wt0 = –p/4 = _ 45. Соответственно, iL(t0–) = iL(t0+) = 0,193sin(– 45 + 5,42) =
= – 0,123; uC (t0+) = uC (t0–) = 0,689sin(– 45 – 58) = – 0,671.
В последующем расчете начало отсчета t0 примем за ноль, тогда iL(t0+) = iL(0+) = – 0,123 А, uC (t0+) =
= uC (0+) = – 0,671 В.
Характер переходного процесса зависит от корней характеристического уравнения. Характеристическое уравнение составим методом входного сопротивления: Z( p) = R1 + pL + R3 + (R2 / pC ) /
/ (R2 + 1 / pC) = 0. После преобразования получим Z( p) = p2 +
+ p[(R1R2C + L) / (R2LC )] + (R1 + R2) / ( R2LC ) = 0. Введем обозначения и рассчитаем
d = (R1R2C + L) / (2R2LC ) = 800, 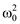 = (R1 + R2) / (R2LC) = 630 000: p2 + 2dp +
= (R1 + R2) / (R2LC) = 630 000: p2 + 2dp + 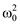 = p2 + 2800p + 630 000 = 0, корни p1,2 = – d
= p2 + 2800p + 630 000 = 0, корни p1,2 = – d 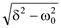 = _ 800
= _ 800 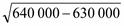 = – 800 100, p1 = – 700 с–1, p2 = – 900 с–1.
= – 800 100, p1 = – 700 с–1, p2 = – 900 с–1.
На основании полученных корней запишем выражения для токов, напряжений и их производных (так как система второго порядка) в общем виде:
y(t) = yсв + yвын=A1exp( p1t) + A2exp( p2t) + yвын;
dy(t)/dt = p1A1exp( p1t) + p2A2exp( p2t) + dyвын/dt. (1)
Для определения зависимых начальных условий и установившихся значений токов и напряжений составим систему уравнений согласно законам Кирхгофа, которая будет справедлива на интервале
0+ t :
u12(t) = R1i1 + uL + R3i1 + uC, uC – R2i2 = 0, i1 = i2 + i3. (2)
Первый интервал 0+ t T/2– : u12(t) = 20 В.
Найдем зависимые начальные условия для момента коммутации ключа t0+, для которого
iL(0+) = i1(0+) = – 0,123 А, uC (0+) = – 0,671 В: i2(0+) = – 0,0839 А, i3(0+) = – 0,207 А, uL (0+) = 27,436 В.
Определим вынужденные значения (t = ) токов и напряжений из уравнений (2), зная, что при постоянном (не изменяющемся во времени) воздействии uL() = 0, i3() = iС () = 0. Получим:
i1() = u12 / (R1 + R2 + R3) = 0,317 А, uC () = i1()R2 = 2,54 В.
Составим уравнения для определения постоянных интегрирования выражений i1(t) и uL(t) согласно (1): i1(0+) = A1 + A2 + i1(), uL(0+) = L(di1/dt)(0+) = L(p1A1 +p2A2) + uL(); –0,123 = A1 + A2 +
+ 0,317; 27,436 = 0,05[(–700) A1 + (– 900) A2] + 0. Решая уравнения, найдем A1 = 0,761, A2 = – 1,202. Окончательно решение для i1(t) и uL(t): i1(t) = (0,761e–700t – 1,202e–900t + 0,317) А, uL(t) = (–26,635e–700t +
+ 54,1202e–900t) В.
Аналогично, используя начальные и вынужденные значения, найдем решение для uС (t) и i3(t) = iС (t) = СduС / dt на первом интервале входного воздействия:
uС (t) = (– 15,24e–700t + 12,02e–900t + 2,54) В; i3(t) =
=(2,665e–700t – 2,704e–900t) А; u2(t) = uС(t) + i1(t)R3 = (– 7,63e–700t + 5,715) В.
Второй интервал T/2+ t T– : u12(t) = – 20 В.
Скачкообразное изменение входного напряжения в момент
t = T/2 создало новые условия для протекания переходного процесса. Методика расчета аналогична методике для первого интервала. Прежними остаются только корни, так как структура и параметры элементов схемы не изменились, а напряжение источника входного воздействия на корни не влияет.
Независимые начальные условия uC (T/2+) и iL(T/2+) = i1(T/2+) определим из uC (t) и iL(t) первого интервала: uC (T/2+) = uC (T/2–) = (–15,24e–700T/2 + 12,02e–900T/2 + 2,54) = 1,56, i1(T/2+) = i1(T/2–) =
= (0,761e–700T/2 – 1,202e–900T/2 + 0,317) = 0,331, T/2 = 3,14 10–3 с.
Зависимые начальные условия и вынужденные значения токов и напряжений вычислим, воспользовавшись уравнениями (2): i2(T/2+) = 0,195 А, i3(T/2+) = 0,136 А, uL(T/2+) = – 39,765 В; uL() = 0 В, i3() = 0 А, i1() = i2() = u12 / (R1 + R2 + R3) = – 0,317 А, uC() = R2i2() = – 2,54 В.
Решение для i1(t) и u2(t) найдем, используя uC (t) и iC (t) и уравнения (2). С учетом смещения процессов по оси времени относительно начала отсчета получим: uC (t) = uCсв + uCвын = A1
exp[p1(t – T/2)] + A2 exp[p2(t – T/2)] + uCвын; iC(t) = CduC (t) / dt =
= Cp1A1exp[(p1(t – T/2)] + Cp2A2exp[(p2t – T/2)]+ iCвын.
При t = (T/2+): uC (T/2+) = A1 + A2 + uCвын(T/2+); iC (T/2+) = Cp1A1 + Cp2A2 + iCвын(T/2+). Подставляя в эту систему начальные и вынужденные значения токов и напряжений, найдем постоянные интегрирования: – 1,56 = A1 + A2 – 2,54; 0,136 = 0,05(– 700)A1 + 0,05 (– 900) A2; A1 = 21,17; A2 = –17,07. Следовательно,
uC (t) = {21,17exp[–700(t – T/2)] – 17,07exp[–900(t – T/2)] – 2,54} B;
iC(t) = i3(t) = {–3,705exp[(–700(t – T/2)] + 3,841exp[(–900(t – T/2)]} A;
i2(t) = uС (t)/R2 = {2,646exp[–700(t – T/2)] – 2,134exp[–900(t – T/2)] –
– 2,54} A; i1(t) = i2(t) + i3(t) = {– 1,06 exp[–700(t – T/2)] + 1,71 exp[– 900(t – T/2)] – 0,317} A;
u2(t) = u С(t) + i1(t)R3 = {10,58 exp[– 700(t – T/2)] – 5,715} B.
Чтобы убедиться в правильности полученных результатов, выполним проверку:
1. Определим из найденных решений значения i1(T/2–) и i1(T/2+). Согласно закону коммутации, i1(t) = iL(t) не может измениться скачком, т.е. i1(T/2–) = i1(T/2+): i1(T/2–) = 0,331 А, i1(T/2+) =
= 0,3305 А — равенство соблюдается с достаточной точностью.
2. Изменение входного напряжения u12(t) в момент t = T/2 на (–2U12) = – 40 B может уравновесить в данной схеме только напряжение на индуктивность, так как остальные напряжения скачком измениться не могут, следовательно, uL(T/2+) – uL(T/2–) = – 40. Проверим, используя найденные решения:
uL(T/2+) = u12(T/2+) – uС(T/2+) – i1(T/2+)(R1 + R3) = – 39,765 В, uL(T/2–) = 0,248 В, uL(T/2+) – uL(T/2–) =
= –39,765 – 0,248 = –40,013 В — результаты совпадают с достаточной точностью. При первой коммутации изменение напряжения на индуктивном элементе 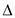 UL должно равняться 20 В (проверьте!).
UL должно равняться 20 В (проверьте!).
