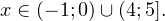Решение логарифмических уравнений и неравенств

О:Логарифмом числа b по основанию числа a (a≠1) называется число x, такое, что a^x=b (числа a и b положительные).

Записывается log_ab=x, где a - основание логарифма, x - логарифмируемое число.

Основное логарифмическое тождество: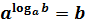

Свойства логарифмов:

1. log_a(b∙c)=log_ab+ log_ac

2. log_a 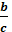= log_ab- log_ac

3. log_ab^p = plog_ab

4. log_ab= 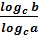,c≠1

5. log_ab= 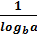, b≠1

6. log_a1=0

7. log_aa=1

Таблица степеней чисел

Число степень
									и т.д.

Уравнения, содержащие неизвестную переменную под знаком логарифма, называются логарифмическими уравнениями(т.е.уравнения вида log_ax = b, где x > 0, а > 0 и а ≠ 1 называются логарифмическими)

Чтобы решить логарифмическое уравнение или неравенство, нужно:

1. найти ОДЗ (область допустимых значений) логарифма: log_ab=x, a^x=b ОДЗ: a>0; a≠1 (если а - неизвестно), b>0.

2. Решить само уравнение или неравенство

Рассмотрим 3 типа логарифмических уравнений:

· уравнения содержащие один логарифм, в основе решения лежит определение логарифма;

· уравнения, содержащие два уравнения и более; в основе решения лежит условие равенства логарифмов: 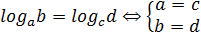(логарифмы равны тогда и только тогда, когда равны их основания и выражения под знаками логарифма);

· уравнения, сводящиеся к квадратным алгебраическим; в основе решения лежит введение новой переменной, позволяющей преобразовать логарифмическое уравнение в квадратное алгебраическое.

Пример 1. Решить уравнение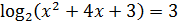

Решение: данному уравнению удовлетворяют те значения x, для которых выполнено равенство 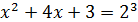. Получили квадратное уравнение 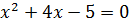, корни которого равны 1 и -5. Следовательно, числа 1 и -5 – решения данного уравнения.

Пример 2. Решить уравнение .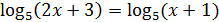

Решение:

ОДЗ: ;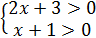

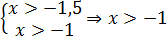
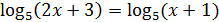равносильно 2x+3=x+1, находим х=-2, -2 не удовлетворяет ОДЗ 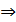данное уравнение корней не имеет.

Пример 3. Решить уравнение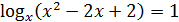

ОДЗ: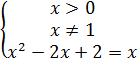

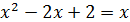
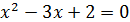, полученное квадратное уравнение имеет корни х1=1и х2=2, х1 не удовлетворяет условию ОДЗ, следовательно решением уравнения является х2=2

Пример 4. Решить уравнение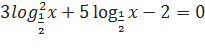

Решение: ОДЗ: x > 0.

Используем подстановку: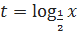

Уравнение принимает вид:

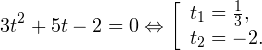
Обратная подстановка:

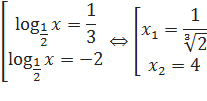
х1 и х2 Î ОДЗ, следовательно решением уравнения является 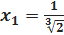и

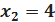
Логарифмирование и потенцирование.

Логарифмирование (пример 2) и потенцирование(пример 3).

Пример 5. Прологарифмировать по основанию 5 выражение 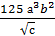, где a, b, c – положительные числа.

Решение: Используя свойства логарифмов (с1, с2), получим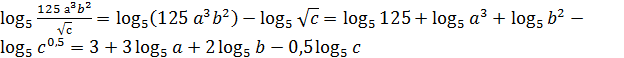

Пример 6. Найти х, если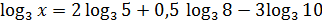

Решение: 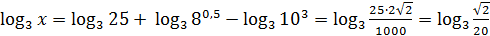из равенства 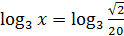находим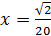

Рассмотрим примеры решения логарифмических неравенств:

Для решения неравенств рассмотрим теорему

Теорема: Если f(x) > 0и g(x) > 0, то: при a> 1 логарифмическое неравенство log a f(x) > log a g(x)равносильно неравенству того же смысла: f(x) > g(x); при 0 < a < 1 логарифмическое неравенство log a f(x) > log a g(x) равносильно неравенству противоположного смысла: f(x) < g(x).

Пример 7. Решить неравенство: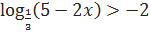

Решение:

Число -2= 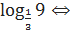неравенство можно записать в следующем виде: 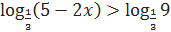. Логарифмическая функция с основанием определена и убывает на 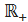, так как 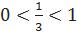, следовательно неравенству 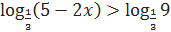удовлетворяют такие числа x, для которых выполнено условие 0<5-2x<9, откуда -2<x<2,5. Решением будет интервал (-2; 2,5)

Пример 8. Решить неравенство: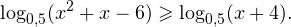

Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:

ОДЗ: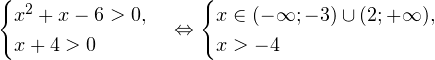

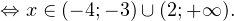
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме будет переход к следующему квадратичному неравенству:

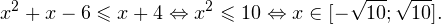
Следовательно , с учетом области допустимых значений решением будет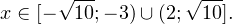

Пример 9. Решить неравенство:

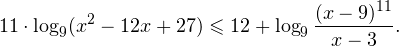
Решение. Найдем ОДЗ:

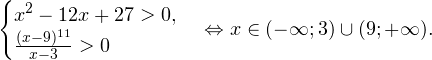
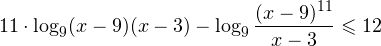
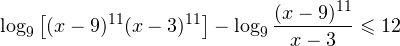
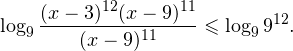
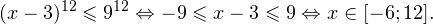
Следовательно, с учетом области допустимых значений решением будет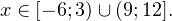

Пример 10. Решить логарифмическое неравенство:

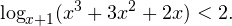
Решение.ОДЗ:

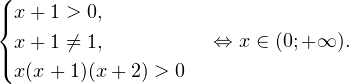
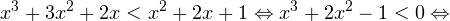
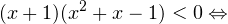
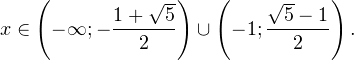
Следовательно, с учетом области допустимых значений решением будет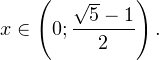

Пример 11. Решить неравенство:

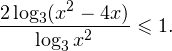
Решение.

ОДЗ:

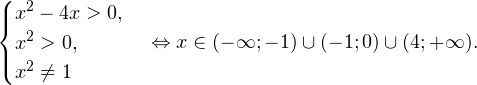
I способ.Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:

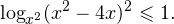
Неравенство будет равносильно двум системам. Первой:

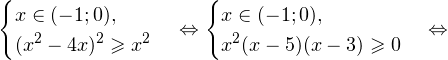
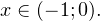
И второй:

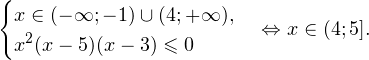
Следовательно, с учетом области допустимых значений решением будет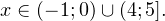

II способ.Решаем методом интервалов. Преобразуем неравенство к виду:

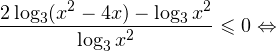
Вычтем из знаменателя 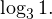Это ничего не изменит, поскольку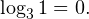

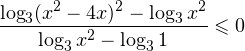
Т.К. выражения и — одного знака при 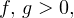в области допустимых значений имеет место следующий равносильный переход:

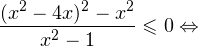
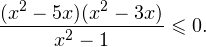
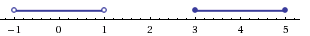
Множество решений данного неравенства

Итак, 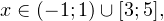а с учетом области допустимых значений решением будет