Основные теоретические сведения и расчетные формулы

При изгибе в поперечном сечении бруса, который в этом случае называется балкой, возникают два внутренних усилия: попе­реч­ная си­­­ла Q и изгибающий момент M_z.

Поперечной силой в сечении называется внутреннее усилие, численно ра­­­­­в­­­­­ное алгебраической сумме проекций всех сил, действующих на балку по одну сторону от рассматриваемого сечения, на нормаль к оси балки. По­­­­­перечная сила считается положительной, если она стремится вращать бес­­­­конечно малый элемент балки по ходу часовой стрелки. Обратное на­пра­в­ление вращения соответствует отрицательной поперечной силе (Рисунок 14).

Рисунок 14 - Правило знаков для поперечной силы

Изгибающим моментом в сечении балки называется внутреннее усилие, численно равное алгебраической сумме моментов внешних сил, действующих на балку по одну сторону от рассматриваемого сечения, относительно его центра тяжести. Изгибающий момент положителен, если под его воздействием балка изгибается выпуклостью вниз; при изгибе выпуклостью вверх изгибающий момент считается отрицательным (Рисунок 15). Эпюра изгибающего момента строится со стороны сжатого волокна балки, которое находится с вогнутойчасти балки. Положительные значения изгибающего момента откладываются вверх от оси эпюры, отрицательные - вниз.

Примечание: Студенты строительных специальностей строят эпюру изгибающего момента со стороны растянутого волокна, что не влияет на результаты расчетов балок на прочность и жесткость.

Рисунок 15 - Правило знаков для изгибающего момента

При решении задач, связанных с расчетами балок на прочность и жесткость, строятся графики изменения этих усилий по длине бруса - эпю­ры поперечных сил и изгибающих моментов. Целью построения эпюр при расчетах на прочность является нагля­д­ное представление изменения внутренних усилий в сечении в зависимости от его положения и определение на­­иболее нагруженных участков балки.

Для того чтобы установить закон изменения внутренних усилий по дли­не балки, выбирается прямоугольная система координат, ось абсцисс x направляется вдоль оси балки, а оси y, z совмещаются с главными цент­раль­ными осями инерции поперечного сечения. Затем записываются аналитические выражения для поперечной силы и изгибающего момента в виде функций от абсциссы x, определяющей поло­же­­ние рассматриваемого сечения. Соста­вив уравнения Q(x) и M_z(x), аб­сцис­сам дают последовательно конкретные значения и вычисляют вели­чины Q и M_z,, откладывая их в принятом масш­табе от оси эпюры вверх или вниз, строя, таким образом, графики функций Q(x) и M_z(x) - эпюры по­перечных сил и изгибающих моментов.

При изгибе балки в ее поперечном сечении возникают нормальные и касательные напряжения. Нормальные напряжения определяются по формуле

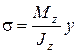, (5.1)

где M_z - изгибающий момент в рассматриваемом сечении;

J_z - момент инерции поперечного сечения относительно нейтральной оси;

y - расстояние от нейтральной оси до точки, где определяется напряжение.

Условие прочности при изгибе для пластичных материалов

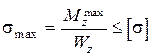, (5.2)

где 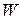_z - осевой момент сопротивления при изгибе, вычисляемый относительно нейтральной оси. Для простых геометрических фигур его вычисляют по формулам:

для прямоугольника ;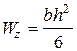

для круга .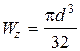

Моменты сопротивления прокатных профилей приводятся в таблицах сор­та­мента. Для хрупких материалов (чугун, высокоуглеродистые стали), имеющих сущес­т­венно различные пределы проч­н­ости при растяжении 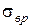и сжатии 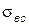, тре­буется проверка их прочности по на­и­­большим растягивающим 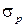и наи­боль­шим сжимающим напряжениям :

,

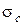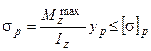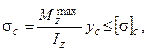
где 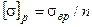, 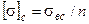; n- запас прочности.