Построение кривой по точкам

Метод линеаризации данных для y=Ce^Ax

Предположим, что заданы точки (x_1,y₁),(x_2,y₂),…,(x_N,y_N) и требуется выполнить подгонку экспоненциальной кривой вида

(9) y=Ce^Ax.

Первым будет шагом будет логарифмирование обеих частей:

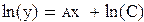(10)

Затем заменим переменные:

(11)

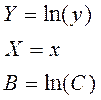
В результате получим линейное соотношение между новыми переменными X и Y:

(12)

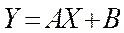
Исходные точки (x_k;y_k) на плоскости ху преобразовались в точки (X_k;Y)=(x_k;ln(y_k)) на плоскости XY. Этот процесс называют линеаризация данных. Тогда построенная МНК линия является подгонкой к точкам {(X_k;Y_k)}.Нормальными уравнениями для нахождения А и В будут уравнения

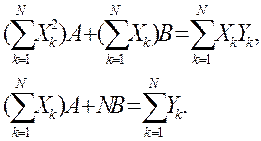
После того как А и В найдены, вычисляем параметр С уравнения (1):

(13)

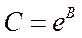
Пример расчета в пакете MATHCAD

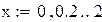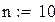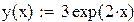Разбиваем и получаем точки Χ и Υ

Табулируем:

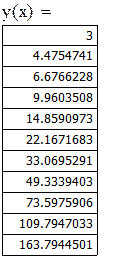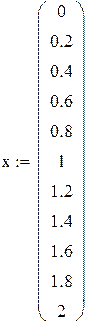
Решение МНК с помощью встроенных функций:

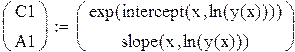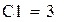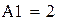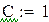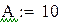Получаем результат при помощи блока Given:

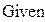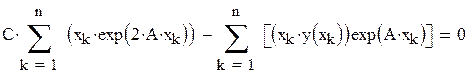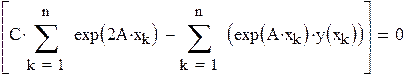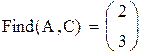Практическая задача

Задание: необходимо написать программу для определения гравитационной постоянной g следующих совокупностей данных. Используем подгонку нелинейного МНК

Время, tk	Расстояние, dk
0.200	0.1960
0.400	0.7835
0.600	1.7630
0.800	3.1345
1.000	4.8975

Реализация метода в MATLAB

function z=E(u)

A=u(1);

C=u(2);

z=(C.*exp(0.2*A) -0.1960).^2+(C.*exp(0.4*A)-0.7835).^2+(C.*exp(0.6*A)-1.7630).^2+( C.*exp(0.8*A)-3.1345)+( C.*exp(1.0*A)-4.8975)

>> fmins(‘E’,[1 1])

ans =

0.1271 3.9115

Т.е. y=0.1271e^3.9115

Реализация метода в MATHCAD:

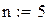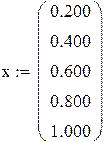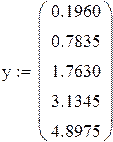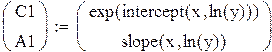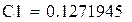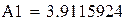Пояснения:

1) Представим, что время и расстояние х и у.

2) Решаем МНК с помощью встроенных функций.

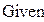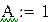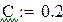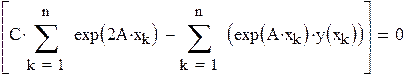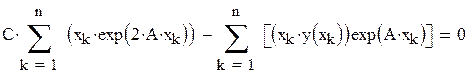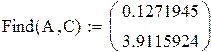3) Получаем результат при помощи блока Given. Результат- это и есть гравитационная постоянная. Которую мы представляем как

y=0.1271e^3.9115

Варианты лабораторных работ

Номер варианта	Функция	Номер варианта	Функция

ТЕМА 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Лабораторная работа № 3

Приближенное вычисление определенных интегралов»

Цель работы.Вычислить численно определенный интеграл вида

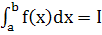, где (1)

- а, b – нижний, верхний пределы интегрирования соответственно;

- f(х) - непрерывная функция на отрезке [а, b].

с помощью методов левах, правых, средних прямоугольников, трапеций и Симпсона.Оценить погрешность полученных результатов.

Постановка задачи:

1. С помощью различных сред программирования (MathCad, MATLAB) найти приближенное значение определенного интеграла функции f(x) на интервале [a, b] при заданном числе промежутков интегрирования n .

2. Приближенное значение интеграла определить с помощью методов левах, правых, средних прямоугольников, трапеций и Симпсона.

3. Оценить погрешность вычисления приближенного интеграла.

Содержание отчета:

1. Постановка задачи.

2. Теоретические сведения.

3. Ручной счет с использованием формул средних прямоугольников, трапецій.

4. Листинги счета на ЭВМ.