Теорема о связи функции и ее предела. Основные свойства предела( предел сумма, произведения, частного)
Й, 2й замечательный пределы.
 1й: limsinx/x=1, limx/sinx=1. x®0
1й: limsinx/x=1, limx/sinx=1. x®0
j
lim((Sina)/a)=1
x®0
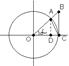
SDOAC<SсектораOAC<SDOCB
SDOAC=1/2*OC*AD, OA=OC=1, то
SDOAC=1/2*OC*OA*Sina=1/2*Sina
SсектораOAC=1/2*OA*OC*a=1/2*a(т.к. OA=OC)
SDOCB=1/2*OC*BC=1/2*OC*OC*tga=1/2*tga
1/2*Sina<1/2*a<1/2tga //*2
sina<a<tga//:sin
1<a/sina<1/cosa, =>cosa<sina/a<1,
limCosa<lim((Sina)/a)<lim1, по признаку
a®0 a®0 существования предела ф-ции lim((Sina)/a)=1a®02ой: lim(1+1/n)n=e»2.7183
n®¥
Зная, что 1/n=a - б.м.в., то n=1/a и
x®¥ a®0
lim(1+1/n)1/a=e
a®0
Функция и ее пределы. Теорема о промежуточных функциях
Вторая Теоре́ма Больца́но — Коши́ о промежуточных значениях непрерывной функции в математическом анализе и общей топологии — это утверждение, что если непрерывная функция принимает два значения, то она принимает и любое значение между ними.
Пусть дана непрерывная функция на отрезке 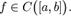 Пусть также
Пусть также 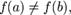 и без ограничения общности предположим, что
и без ограничения общности предположим, что 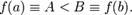 Тогда для любого
Тогда для любого 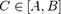 существует
существует 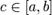 такое, что f(c) = C.
такое, что f(c) = C.
Теорема о связи функции и ее предела. Основные свойства предела( предел сумма, произведения, частного)
свойства:Предел суммы равен сумме пределов: 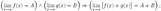 предел разности равен разности пределов
предел разности равен разности пределов 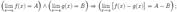 Предел произведения равен произведению пределов
Предел произведения равен произведению пределов 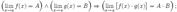 Предел частного равен частному пределов.
Предел частного равен частному пределов. 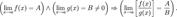
29)Бесконечно малые и бесконечно большие функции. Свойства эквивалентности Если 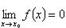 , то функция f называется бесконечно малой при x → x0; если , то функция f называется бесконечно малой при x → x0; если 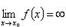 , то функция f называется бесконечно большой при x → x0. , то функция f называется бесконечно большой при x → x0. |
Две бесконечно малые называются эквивалентными, если предел их отношения равен1 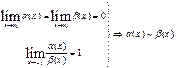
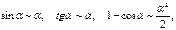
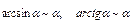 .
. 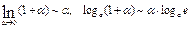
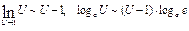 30) 1 замечательный предел. Раскрытие неопределенности 0/0.(1 предел см 26)
30) 1 замечательный предел. Раскрытие неопределенности 0/0.(1 предел см 26)
Неопределенность вида 0/0. Первое правило Лопиталя. Раскрытие 0/0. 1-е правило Лопиталя. Если lim(x®a)f(x)= lim(x®a)g(x), то lim(x®a)f(x)/g(x)= lim(x®a)f‘(x)/g‘(x), когда предел $ конечный или бесконечный.
31)2 замечательный предел для функции. Раскрытие неопределенностей 1 в стп. Бескон. Другие не определенности2ой: lim(1+1/n)n=e»2.7183
n®¥
Зная, что 1/n=a - б.м.в., то n=1/a и
x®¥ a®0
lim(1+1/n)1/a=e
a®0
Раскрытие ¥/¥. Второе правило.Если lim(x®a)f(x)= lim(x®a)g(x)=¥, то lim(x®a)f(x)/g(x)= lim(x®a)f‘(x)/g‘(x). Правила верны тогда, когда x®¥,x®-¥,x®+¥,x®a-,x®a+.Неопред-ти вида 0¥, ¥-¥, 0^0, 1^¥, ¥^0.
Неопр. 0¥, ¥-¥ сводятся к 0/0 и ¥/¥ путем алгебраических преобразований. А неопр.0^0, 1^¥, ¥^0 с помощью тождества f(x)^g(x)=e^g(x)lnf(x) сводятся к неопр вида 0
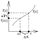 32)Функции, непрерывные в точке. Классификация точек разрыва
32)Функции, непрерывные в точке. Классификация точек разрыва
x=x0+Dx, Dx=x-x0
Dy=f(x0+Dx)-f(x0)
Ф-ция y=f(x) наз. непрерывной в точке x0, если она определена в окрестности этой точки, а limDy=0. (б.м. приращению аргумента соответствует б.м. приращению ф-ции).
limDy=lim[f(x)-f(x0)]=limf(x)-limf(x0)=0, то
limf(x)=limf(x0)
x®x0
Ф-ция непрерывна в точке х0, если ее предел = значению этой ф-ции в точке х0
Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке. Точки, где функция f(x) не является непрерывной, называются точками разрывафункции f(x).
Дописать
