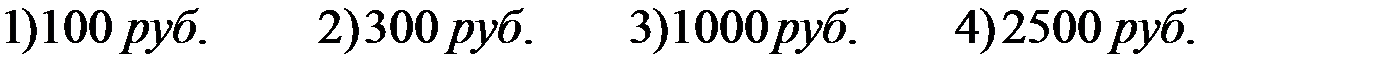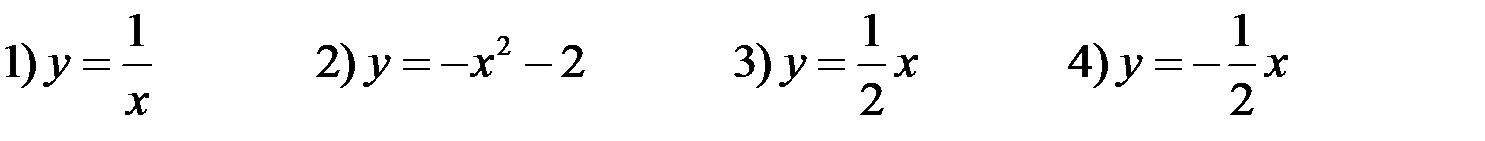Модуль «РЕАЛЬНАЯ МАТЕМАТИКА». Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого
14. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России на 1 января 2013 года.
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 112 км/ч на участке дороги с максимальной разрешённой скоростью 90 км/ч? Размер штрафа, руб.
| ||||||||||||||||||||||||||||||||
15. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат – крутящий момент в Н  м. Чему равен крутящий момент (в Н м. Чему равен крутящий момент (в Н  м), если двигатель делает 1000 оборотов в минуту? м), если двигатель делает 1000 оборотов в минуту? 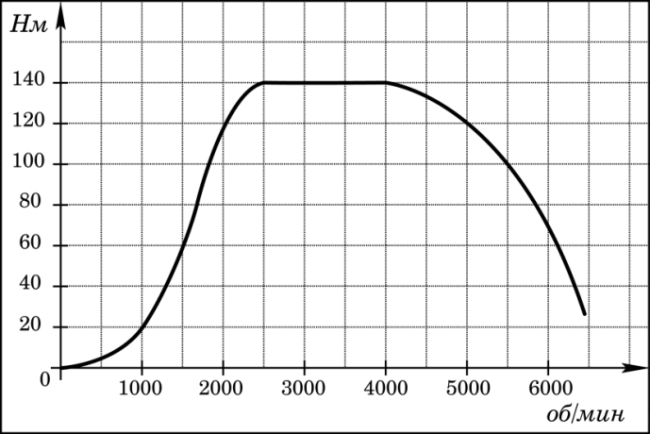 | ||||||||||||||||||||||||||||||||
16. Перед представлением в цирк для продажи было заготовлено некоторое количество воздушных шариков. Перед началом представления было продано 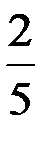 всех воздушных шариков, а в антракте – еще 52 штук. После этого осталась треть всех шариков. Сколько шариков было первоначально? всех воздушных шариков, а в антракте – еще 52 штук. После этого осталась треть всех шариков. Сколько шариков было первоначально? | ||||||||||||||||||||||||||||||||
| 17. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка – 3 км/ч. Какое расстояние (в километрах) будет между ними через 30 минут? | ||||||||||||||||||||||||||||||||
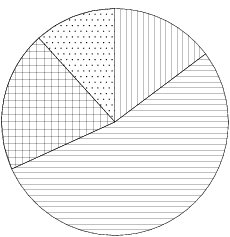
18. На диаграмме показан возрастной состав населения России. Определите по диаграмме, население какого возраста преобладает.
| ||||||||||||||||||||||||||||||||
| 19. В фирме такси в данный момент свободно 15 машин: 3 черных, 6 желтых и 6 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. | ||||||||||||||||||||||||||||||||
20. Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле 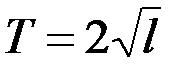 , где l – длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды. , где l – длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды. |
Часть 2
Модуль «АЛГЕБРА»
21. Упростите выражение 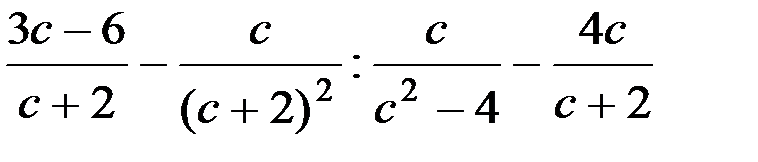 |
22. Найдите значения а, при которых система уравнений 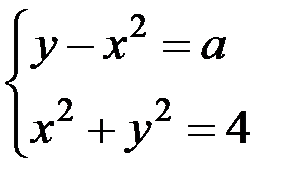 имеет три решения. имеет три решения. |
| 23. Два строителя выложили стену из кирпичей за 14 дней, причем второй присоединился к первому через 3 дня после начала работы. Известно, что первому строителю на выполнение всей работы потребовалось бы на 6 дней больше, чем второму. За сколько дней мог бы выложить эту стену каждый строитель, работая отдельно? |
Модуль «ГЕОМЕТРИЯ»
| 24. В трапеции ABCD (AD||BC), BC=9дм, AD=16дм, BD=18дм. О – точка пресечения AC и BD. Найдите ОВ. |
| 25. Середина отрезка BD является центром окружности с диаметром AC, причем точки A, B, C, D не лежат одной прямой. Докажите, что ABCD – параллелограмм. |
| 26. В ромбе ABCD диагонали равны 5см и 12см. На диагонали AC взята точка M так, что АМ:МС=4:1. Найдите площадь треугольника AMD. |
Вариант 3.2.
Часть 1
Модуль «АЛГЕБРА»
1. Найдите значение выражения 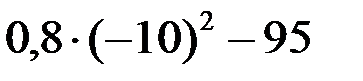 | ||||||
2. На координатной прямой изображены числа a и c. Какое из следующих неравенств неверно?  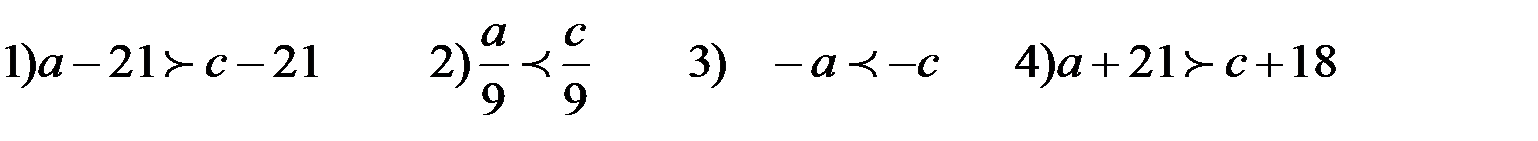 | ||||||
3. Найдите значение выражения: 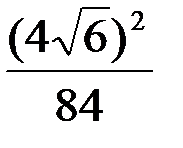 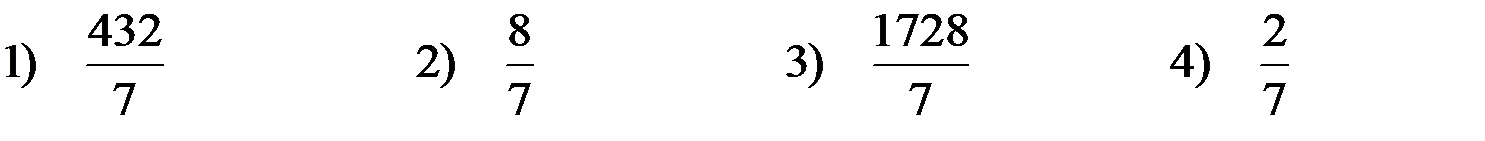 | ||||||
4. Решите уравнение: 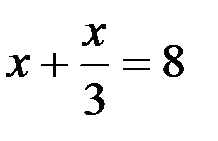 | ||||||
5. Установите соответствие между графиками функций и формулами, которые их задают. Графики
Формулы
| ||||||
6. Геометрическая прогрессия 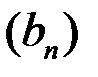 задана условиями задана условиями 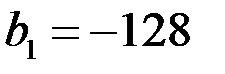 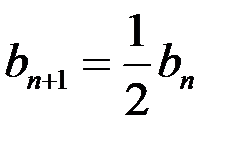 . Найти . Найти 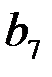 . . | ||||||
7. Упростите значение выражения 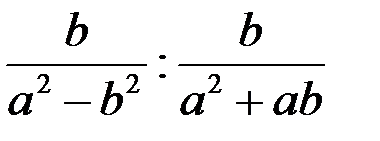 и найдите его значение при и найдите его значение при 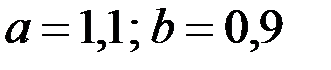 . . | ||||||
8. Решение какого из данных неравенств изображено на рисунке  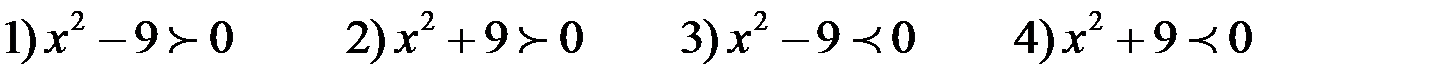 |
Модуль «ГЕОМЕТРИЯ»