Центр параллельных сил

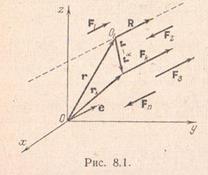В этой главе рассматриваются такие системы параллельных сил, которые приводятся к равнодействующей. Прежде всего нужно отметить, что условия приведения системы параллельных сил к равнодействующей сводятся к одному неравенству 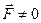. Действительно, уже было показано, что второй инвариант системы параллельных сил тождественно равен нулю. Поэтому единственным условием приведения пространственной системы параллельных сил к равнодействующей является неравенство нулю главного вектора этой системы

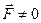. (8.1)

Считая это условие выполненным, выясним, что происходит с равнодействующей 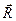при одновременном повороте линий действия данных параллельных сил на один и тот же угол, если точки приложения этих сил сохраняются неизменными и повороты линий действия сил происходят вокруг параллельных осей.

При этих условиях равнодействующая заданной системы сил также одновременно поворачивается на тот же угол, причем поворот происходит вокруг некоторой фиксированной точки, которая называется центром параллельных сил. Перейдем к доказательству этого утверждения.

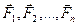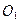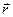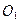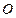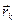Предположим, что для рассматриваемой системы параллельных сил главный вектор не равен нулю, следовательно, данная система сил приводится к равнодействующей. Пусть точка есть какая-либо точка линии действия этой равнодействующей. Пусть теперь – радиус-вектор точки относительно выбранного полюса , а – радиус-вектор точки приложения силы .

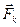Согласно теореме Вариньона сумма моментов всех сил системы относительно точки 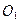равна нулю:

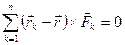, (8.2) так как точка 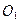лежит на линии действия равнодействующей.

Полученное равенство можно переписать в следующей форме:

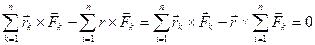. (8.3)

Введем теперь в рассмотрение единичный вектор 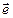, параллельный линиям действия сил. Тогда любая сила 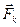может быть представлена в виде

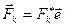, (8.4)

где 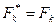, если направление силы 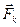и вектора 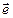совпадают, и 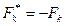, есл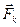и и 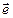направлены противоположно друг другу. Очевидно, что при этом

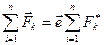. (8.5) Подставляя выражения (8.4) и (8.5) в соотношение (8.3), получим

,

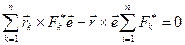откуда

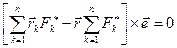. (8.6)

Последнее равенство удовлетворяется при любом направлении сил (т.е. направлении единичного вектора 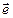) только при условии, что первый множитель равен нулю:

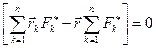. (8.7)

В свою очередь это равенство имеет единственное решение относительно радиус-вектора 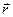, определяющего такую точку приложения равнодействующей, которая не меняет своего положения при повороте линий действия сил. Такой точкой и является центр параллельных сил, чем и доказывается его существование. Обозначив радиус-вектор центра параллельных сил через 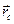, из равенства (8.7) получим

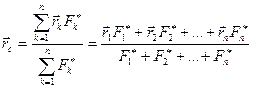. (8.8)

Пусть 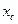, , 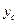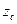– координаты центра параллельных сил, а 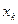, , 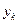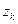– координаты точки центра приложения произвольной силы 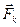; тогда координаты точки центра параллельных сил найдутся из формул:

,

,

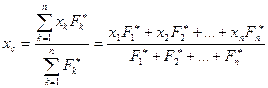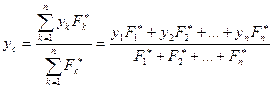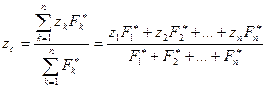. (8.9)

Выражения

, ,

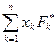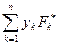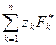
называются соответственно статическими моментами заданной системы сил относительно координатных плоскостей , , .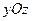

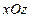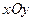Отметим, что если начало координат выбрано в центре параллельных сил, то

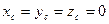
и статические моменты заданной системы сил равны нулю.

Центр тяжести

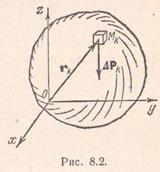
Тело произвольной формы, находящееся в поле сил тяжести, можно разбить сечениями, параллельными координатным плоскостям, на элементарные объемы. Если пренебречь размерами тела по сравнению с радиусом Земли, то силы тяжести, действующие на каждый элементарный объем, можно считать параллельными друг другу. Обозначим через 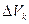объем элементарного параллелепипеда с центром в точке 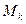, а силу тяжести, действующую на этот элемент, – через 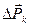. Тогда средним удельным весом элемента объема называется отношение 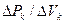. Стягивая параллелепипед в точку 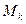, получим удельный вес в данной точке тела, как предел среднего удельного веса

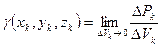. (8.10)

Таким образом, удельный вес является функцией координат, т.е. 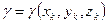. Будем считать, что вместе с геометрическими характеристиками тела задан и удельный вес в каждой точке тела. Вернемся к разбиению тела на элементарные объемы. Если исключить объемы тех элементов, которые граничат с поверхностью тела, то можно получить ступенчатое тело, состоящее из совокупности параллелепипедов. Приложим к центру каждого параллелепипеда силу тяжести 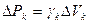, где 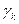– удельный вес в точке тела, совпадающей с центром параллелепипеда. Для системы 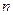параллельных сил тяжести, образованной таким образом, можно найти центр параллельных сил

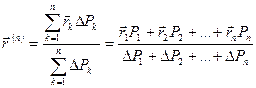. (8.11)

Формула (8.11) определяет положение некоторой точки .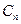

Центром тяжести называется точка, являющаяся предельной для точек 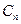при 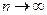. Другим словами, центром тяжести тела называется такая точка, радиус-вектор которой определяется следующим пределом:

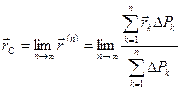(8.12) или, переходя к удельному весу,

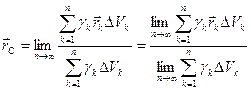. (8.13) При таком предельном переходе предполагается, что размеры всех параллелепипедов стремятся к нулю. Пределы знаменателей в формулах (8.12) и (8.13) равны весу тела

.

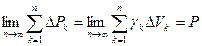Поскольку пределы интегральных сумм в числителе и знаменателе формулы (8.13) представляют собой определенные интегралы, распространенные по объему тела, то 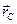можно представить в следующем виде:

.

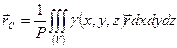Координаты центра тяжести определяются формулами:

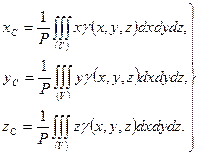(8.14)

Тело называется однородным, если 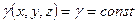. В этом случае величина 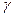выносится в формулах (8.14) за знаки интегралов в числителе и знаменателе и сокращается. Знаменатели в формулах (8.14) после сокращения их на 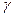равны объему тела 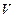. Таким образом, получим

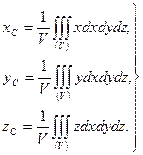(8.15)

Центр тяжести однородного тела часто называют центром тяжести объема.

В ряде случаев тело можно считать тонкой пластиной или оболочкой.

Найдем центр тяжести однородной оболочки, предполагая, что вес элемента ее поверхности пропорционален площади этого элемента

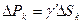
И, следовательно, вес тела 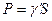( 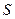– площадь рассматриваемой части поверхности).

Из определения центра тяжести в соответствии с формулами (8.15) получим при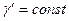

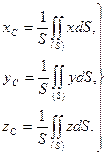(8.16)

Центр тяжести однородной оболочки называют центром тяжести поверхности.

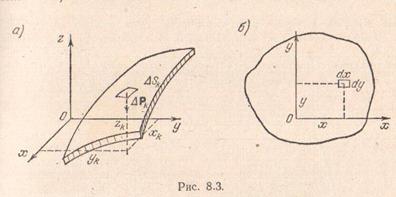
Как следует из формул (8.16), определение координат центра тяжести поверхности связано с вычислением интегралов по поверхности.

Для плоской однородной пластины получим

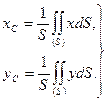(8.17)

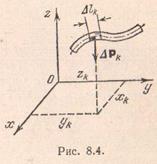Наконец рассмотрим криволинейный стержень – тело удлиненной формы, один из характерных размеров которого значительно больше двух других. Полагая, что вес элемента такого стержня, заключенного между двумя сечениями, нормальными к его оси, пропорционален длине 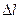дуги этой оси, получим

, ,

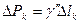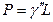где 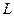– длина стержня.

Величину 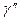называют "погонным весом". При сделанном предположении 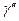– величина постоянная. Тогда в соответствии с формулами (8.15) координаты центра тяжести однородного стержня имеют вид

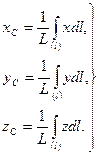(8.18)

Центр тяжести криволинейного стержня называют центром тяжести линии.