Эффективная длительность и эффективная

Ширина спектра сигнала

Литература: [Л.1], с 50-51

[Л.2], с 65-66

[Л.3], с 24-25

Для решения практических задач радиотехники крайне важно знать значения длительности и ширины спектра сигнала, а также соотношение между ними. Знание длительности сигнала позволяет решать задачи эффективного использования времени, предоставляемого для передачи сообщений, а знание ширины спектра – эффективного использования диапазона радиочастот.

Решение указанных задач требует строгого определения понятий «эффективная длительность» и «эффективная ширина спектра». На практике существует большое число подходов к определению длительности. В том случае, когда сигнал ограничен во времени (финишный сигнал), как это имеет место, например, для прямоугольного импульса, определение длительности не встречает затруднений. Иначе обстоит дело, когда теоретически сигнал имеет бесконечную длительность, например, экспоненциальный импульс

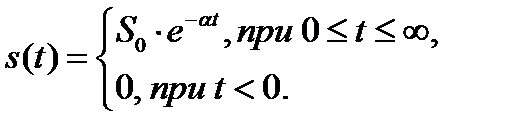
В этом случае в качестве эффективной длительности 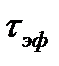может быть принят интервал времени 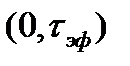, в течение которого значение сигнала 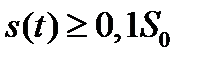. При другом способе в качестве 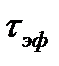выбирают интервал времени, в течение которого 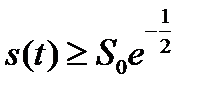. То же самое можно сказать и в отношении определения эффективной ширины спектра .

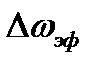Хотя в дальнейшем, некоторые из этих способов будут использоваться при анализе радиотехнических сигналов и цепей, следует отметить, что выбор способа существенно зависит от формы сигнала и структуры спектра. Так для экспоненциального импульса более предпочтителен первый из указанных способов, а для сигнала колоколообразной формы – второй способ.

Более универсальным является подход, использующий энергетические критерии. При таком подходе в качестве эффективной длительности и эффективной ширины спектра рассматриваются соответственно интервал времени и диапазон частот, в пределах которых сосредоточена подавляющая часть энергии сигнала

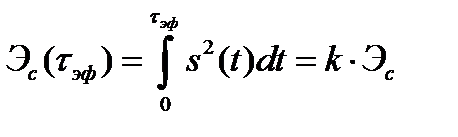, (2.52)

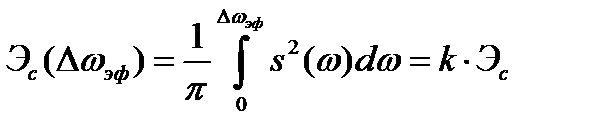, (2.53)

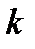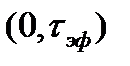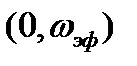где – коэффициент, показывающий, какая часть энергии сосредоточена в интервалах или . Обычно величину 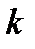выбирают в пределах .

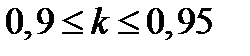Применим критерии (2.52) и (2.53) для определения длительности и ширины спектра прямоугольного и экспоненциального импульсов. Для прямоугольного импульса вся энергия сосредоточена в интервале времен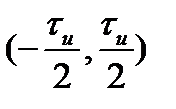и или 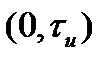, поэтому его длительность 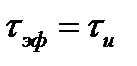. Что касается эффективной ширины спектра, то установлено, что более 90% энергии импульса сосредоточено в пределах первого лепестка спектра. Если рассматривать односторонний (физический) спектр импульса, то ширина первого лепестка спектра составляет 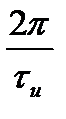в круговых частотах или 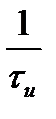в циклических частотах. Отсюда следует, что эффективная ширина спектра прямоугольного импульса равна

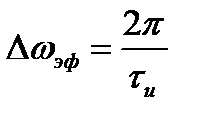или .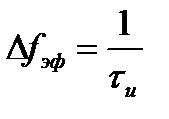

Перейдем к определению 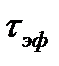и 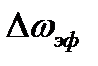экспоненциального импульса. Полная энергия импульса составляет

.

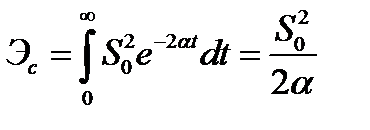Воспользовавшись (2.52), получим

.

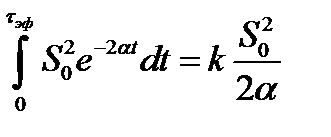Вычислив интеграл в левой части уравнения и решив его, можно прийти к следующему результату

.

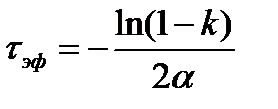Спектр экспоненциального импульса найдем, воспользовавшись преобразованием Фурье

,

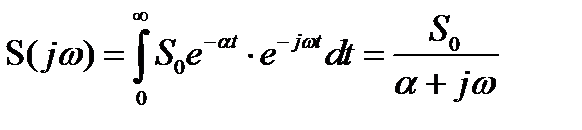откуда следует

.

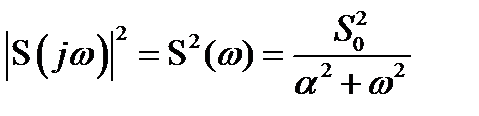Подставляя это выражение в (2.53) и решая уравнение, получим

.

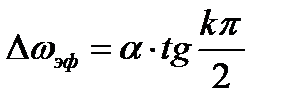Найдем произведение эффективной длительности на эффективную ширину спектра. Для прямоугольного импульса это произведение составляет

,

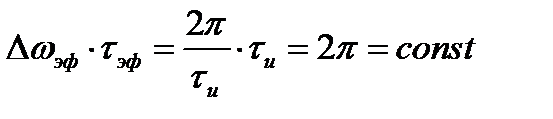или для циклических частот

.

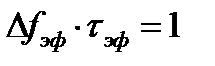Для экспоненциального импульса

.

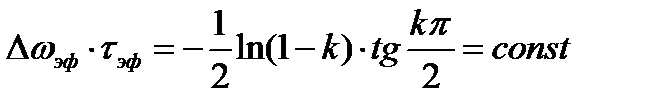Таким образом, произведение эффективной длительности на эффективную ширину спектра одиночного сигнала есть постоянная величина, зависящая только от формы сигнала и величины коэффициента 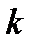. Это означает, что при уменьшении длительности сигнала его спектр расширяется и наоборот. Этот факт уже отмечался пи рассмотрении свойства (2.46) преобразования Фурье. На практике это означает, что невозможно сформировать короткий сигнал, обладающий узким спектром, что является проявлением физического принципа неопределенности.