Поставим задачу: построить для произвольной булевой функции минимальные ДНФ. 1 страница
Булевы функции и способы их задания
Понятие булевой функции.
Определение. Упорядоченный набор  , где
, где  , называется булевым вектором.
, называется булевым вектором.
Числа  называются координатами вектора, число
называются координатами вектора, число  - его длиной. Кратко такой вектор обозначают
- его длиной. Кратко такой вектор обозначают  .
.
Например, (0,0), (0,1), (1,0), (1,1) - булевы векторы длины 2; (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1) - булевы векторы длины 3.
Упражнение 2.1.Сколько существует булевых векторов длины n?
◄ Используем для подсчета правило произведения. Напомним, что звучит оно так: если объект  может быть выбран
может быть выбран  способами и после каждого из таких выборов объект
способами и после каждого из таких выборов объект  в свою очередь может быть выбран
в свою очередь может быть выбран  способами, то выбор «
способами, то выбор «  и
и  » в указанном порядке может быть осуществлен
» в указанном порядке может быть осуществлен  способами.
способами.
При построении конкретного булевого вектора  будем последовательно выбирать n объектов – его координат. Первую координату
будем последовательно выбирать n объектов – его координат. Первую координату  можно выбрать двумя способами, взяв в качестве
можно выбрать двумя способами, взяв в качестве  либо 0, либо 1; вторую координату
либо 0, либо 1; вторую координату  также можно выбрать двумя способами, взяв в качестве
также можно выбрать двумя способами, взяв в качестве  либо 0, либо 1 и т.д., и, наконец, n-ю координату также можно выбрать двумя способами, взяв в качестве
либо 0, либо 1 и т.д., и, наконец, n-ю координату также можно выбрать двумя способами, взяв в качестве  либо 0, либо 1. Таким образом, последовательный выбор n координат можно сделать
либо 0, либо 1. Таким образом, последовательный выбор n координат можно сделать  способами. Следовательно, число булевых векторов длины n равно
способами. Следовательно, число булевых векторов длины n равно  .►
.►
Множество всех булевых векторов длины  называют единичным
называют единичным  -мерным кубом и обозначают
-мерным кубом и обозначают  . Весом вектора называется число его координат, равных 1. Сами векторы называются вершинами куба
. Весом вектора называется число его координат, равных 1. Сами векторы называются вершинами куба  . Расстоянием (Хэмминга) между вершинами
. Расстоянием (Хэмминга) между вершинами  и
и  куба
куба  называется число
называется число  , равное числу координат, в которых они различаются. Вектора
, равное числу координат, в которых они различаются. Вектора  и
и  называются соседними, если
называются соседними, если  , и противоположными, если
, и противоположными, если  .
.
Например, расстояние между векторами  и
и  равно 2. Векторы
равно 2. Векторы  и
и  - соседние, а
- соседние, а  и
и  – противоположные.
– противоположные.
Решив Задачу 2.1, мы показали, что  .
.
Упражнение 2.2. а)Сколько существует булевых векторов длины 16, у которых у которых  ?
?
б)Сколько существует булевых векторов длины  , которые одинаково читаются слева направо и справа налево?
, которые одинаково читаются слева направо и справа налево?
◄ а) Для подсчета используем правило произведения. Чтобы составить требуемый вектор, нам достаточно последовательно выбрать восемь координат  . В качестве каждой из них можно взять одно из двух чисел: 0 или 1. Таким образом, общее число векторов требуемого вида равно
. В качестве каждой из них можно взять одно из двух чисел: 0 или 1. Таким образом, общее число векторов требуемого вида равно  .
.
б) Решить самостоятельно.►
Упражнение 2.3. а)Перечислить булевы векторы длины 4, вес которых равен 2.
б)Найти число булевых векторов длины n, вес которых равен k.
◄ а)  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
б) Каждый такой вектор определяется набором k номеров единичных координат. Каждый такой набор представляет собой неупорядоченную выборку из n элементов по k, в которой элементы не повторяются. Напомним, что такие выборки называются сочетаниями из n элементов по k. Их число равно  .►
.►
Положим  . Число
. Число  называется номером булева вектора.
называется номером булева вектора.
В частности, если  имеем:
имеем:  . Пусть например,
. Пусть например,  , тогда
, тогда  .
.
Упражнение 2.2.Перечислить в порядке возрастания номеров:
а)булевы векторы длины 2;
б)булевы векторы длины 3.
◄ а) Для каждого булева вектора длины 2 вычислим номер:
 ,
,  ,
,
 ,
,  .
.
Следовательно, искомый порядок таков: (0,0), (0,1), (1,0), (1,1).
б)решить самостоятельно.►
Определение. Функция, определенная на  и принимающая значения из множества
и принимающая значения из множества  , называется булевой функцией от
, называется булевой функцией от  переменных.
переменных.
Чтобы задать булеву функцию от  переменных достаточно указать ее значение (0 или 1) для каждого набора
переменных достаточно указать ее значение (0 или 1) для каждого набора  значений аргументов
значений аргументов  . Удобно использовать для этого таблицу истинности:
. Удобно использовать для этого таблицу истинности:
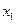 | 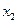 |  |  |  |  |
 |  | ||||
 |  | ||||
 |  | ||||
 |  |  |  |  |  |
 |  |
В каждой строке таблицы вначале дается набор значений переменных  , а затем значение функции на этом наборе. Булевы вектора перечисляются сверху вниз в порядке возрастания номеров.
, а затем значение функции на этом наборе. Булевы вектора перечисляются сверху вниз в порядке возрастания номеров.
Таблицы, задающие булевы функции от одного числа аргументов, отличаются лишь последним столбцом. Поэтому булеву функцию можно задавать вектором значений, который выписывается по правому столбцу ее таблицы истинности. Поскольку помимо строки заголовков таблица содержит  строк (столько, сколько имеется булевых векторов длины
строк (столько, сколько имеется булевых векторов длины  ), то вектор значений булевой функции от
), то вектор значений булевой функции от  переменных имеет длину
переменных имеет длину  .
.
Например, запись  , означает, что
, означает, что  - функция от 2-х переменных и
- функция от 2-х переменных и  ,
,  ,
,  ,
,  .
.
Упражнение 2.5.Сколько существует булевых функций от  переменных?
переменных?
◄ Поскольку каждая булева функция от  переменных однозначно определяется вектором значений длины
переменных однозначно определяется вектором значений длины  , то булевых функций от
, то булевых функций от  переменных столько, сколько булевых векторов длины
переменных столько, сколько булевых векторов длины  , т.е.
, т.е.  . ►
. ►
Множество булевых функций от  переменных обозначают
переменных обозначают  , множество всех булевых функций -
, множество всех булевых функций - 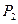 . Решив задачу 2, мы показали, что
. Решив задачу 2, мы показали, что  .
.
Примеры булевых функций
1. Функции одной переменной. Их число:  .
.
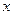 |  |  |  |  |
Приведем обозначения и названия этих функций:
| Обозначение | Название | Прочтение | |
 | константа 0 | «ноль» | |
 | 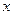 | тождественная функция | « 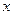 » » |
 |  , , 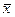 | отрицание | «не 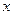 » » |
 | константа 1 | «единица» |
2. Функции двух переменных. Их число:  .
.
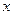 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
Приведем обозначения и названия некоторых функций:
| Обозначение | Название | Прочтение | |
 |  , ,  , ,  | конъюнкция | « 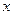 и и  » » |
 |  | сложение по модулю 2 | « 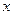 плюс плюс  » » |
 |  | дизъюнкция | « 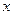 или или  » » |
 |  | стрелка Пирса | «не 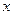 или или  » » |
 |  | эквивалентность | « 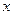 эквивалентно эквивалентно  » » |
 | 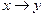 | импликация | « 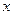 имплицирует имплицирует  » » |
 |  | штрих Шеффера | «не 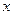 и и  » » |
Функции одной переменной и «именные» функции двух переменных называют основными элементарными функциями. Используемые для их обозначения символы  называют логическими связками (
называют логическими связками ( 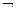 - одноместной, остальные – двуместными).
- одноместной, остальные – двуместными).
Обратите внимание на следующее обстоятельство: есть булевы функции, которые не меняют своих значений при изменении значений некоторых из своих переменных. Например, для функции  имеем:
имеем:  и
и  , т.е. значение переменной
, т.е. значение переменной  не влияет на значение этой функции. А на значения функции
не влияет на значение этой функции. А на значения функции  не влияет значение переменной
не влияет значение переменной 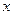 :
:  и
и  . В связи с этим введем понятие фиктивной переменной. Формально оно звучит так.
. В связи с этим введем понятие фиктивной переменной. Формально оно звучит так.
Определение. Переменная 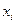 называется фиктивной переменной функции
называется фиктивной переменной функции  , если для всех значений
, если для всех значений  переменных
переменных  выполняются равенства
выполняются равенства  .
.
В противном случае переменная 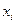 называется существенной.
называется существенной.
Упражнение 2.6.Сформулировать определение существенной переменной.
◄ Переменная 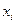 называется существенной переменной функции
называется существенной переменной функции  , если найдется такой набор значений
, если найдется такой набор значений  переменных
переменных  , что
, что  .►
.►
Опыт показывает, что определения лучше усваиваются, если их переформулировать применительно к каким-нибудь частным случаям. Например: переменная  называется фиктивной переменной функции
называется фиктивной переменной функции  , если выполняются четыре равенства
, если выполняются четыре равенства  ,
,  ,
,  ,
, 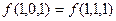 . Или: переменная
. Или: переменная  называется существенной переменной для функции
называется существенной переменной для функции  , если хотя бы одно равенств
, если хотя бы одно равенств  ,
,  ,
,  ,
, 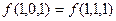 не выполняется.
не выполняется.
Упражнение 2.7.Указать существенные и фиктивные переменные функции:
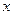 |  |  |
а)  ; б)
; б)  ; в)
; в)  .
.
◄ а) 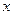 :
:  , следовательно,
, следовательно, 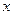 - существенная;
- существенная;
 :
:  и
и  , следовательно,
, следовательно,  - фиктивная.
- фиктивная.
