Термод-кие основы работы тепловых двигателей. Циклы тепловых двигателей, и их эфф-ность. Основные элементы теплового двигателя и принцип преобразования в них энергии

Тепловой двигатель-тепл.машина, в кот. Е подв-ая посредством теплообмена (теплота), с помощью раб тела, преобразуется в мех.энергию (работу).

Тепл.двиг.состоит из: 1)источник теплоты (Т_и), 2) теплоприемник (хо-

лодильник) Т_х < Т_и , 3) раб.тело.

Часто в роли холод –ка выступает окр.среда.

Принцип работы. Закл –ся в преобразовании в механич.работу части теплоты (Q₁-Q₂) в процессе необратимого теплопереноса от ист –ка теплоты к хол –ку за счет прямых круговых процессов, осущ – х с помощью раб.тела.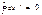

к=2; 1 закон тд.:ΔU=Q^e-L^e;L=Q^e- ΔU.

Полученная работа мб получена из подводимого тепла или убыли внутр.энергии.

А. Работа тепл.двигателя за счет к-л т/д процесса.

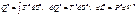
а) Q^e=0, S=const, L=-ΔU

(адиаб.изотропный процесс)

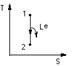
L=-C_v(T₂-T₁)

Работа в этом процессе происходит за счет

↓ внутр.энергии U→L^e.

Внутр.эн.можно превратить в L лишь частично.

В отдельном т/д процессе можно получить ограниченное кол-во работы.

б) Т=соnst, U=f(T), L^e=Q^e (изотерм. процесс)

ΔU=0-для ид. газа

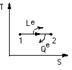
Б.Дв-ли непрерывного (длительного) действия

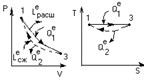
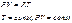
Q_ц =Q₁ –Q₂ >0 (Q₁>Q₂)

L_РАСШ-|L_СЖ|=L_Ц>0;

ΔU=0, L_Ц =Q_ц.

Эф –ть цикла опред –тся терм.КПД: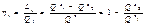

43.Диф Ур тд устанавливают кол-ые характеристики между различными физич свойствами в-ва, вытекающих из основных зак тд. В случае, когда часть параметров оказывается известной, остальные параметры м б найдены путем интегрирования соответствующих дифференциальных уравнений.

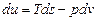(1)

Независимые переменные v и Т:

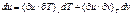-для внутренней энергии (2)

Частные производные входящие в это выражение можно найти ч/з термодинамические параметры и их проихводные. Так из (1) следует, что при Т=const

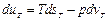,откуда

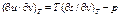(3)

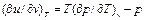(4)

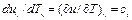(5) ,подставляем (4) и (5) в (2)

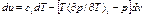(6)

Дифференциальное уравнение для энтропии можно получить совместно решая уравнеия (1) и (6)

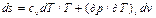
Независимые переменные р и Т: Энтальпия является функцией состояния, поэтому:

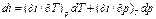
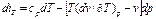
44. Т/д осн. раб.теп.двг. Прямой обратимый цикл Карно и его роль. Сравнение с другими идеальными циклами теп. двг.

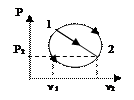
При совер-ии цикла Карно тд-ая сист вд-ет только с 2мя телами, имеющими пост т-ру. Т к имеется 2 тела с постоянными, но разными т-ми Т_I и Т₂(Т₁> Т₂),то одноиз них д б использовано для подвода теплотыq_l к системе, а другое - для отвода теплоты q₂от системы. Тк т-ры тел постоянны, а пр-сы подвода и отвода теплотыд б равновесными, то эти пр-сы м б только изотермными, т. е. протекать при постоянных т-рах T₁=const и Т₂=соnst. Т-ра раб тела в цикле долж изменяться от Т_I до Т₂ без теплообмена с окр ср, т. е. в адиабат процессах. Т о, цикл Карно состоит из двух изотерм и двух адиабат.В пр-се АВ рабочее тело получает кол-во теплоты q₁, в рез-те его энтропия возрастает отзначения s_A до значения s_B на величину Ds_AB=q₁ / T₁. Далее следует адиабатное расширение (линия ВС), в ходе кот т-ра раб те­ла уменьш отТ₁ до Т₂. При т-ре Т₂ протекает изотермный процесс (линия CD), в ходе кот раб тело отдает приемнику такое кол-во теплоты q₂, что энтропия тела отзначения s_C=s_B снова возвращается к значению s_A =s_D; сл-но, Ds_CD= -Ds_AB=q₂/Т₂. Цикл завершается адиабатным сжатием (линия DA), в ходе кот т-ра повыш отT₂ до T₁, принимая первонач значение. Выражение для термического кпд равновесного цикла Карно получается из общвыражения подстановкой в него величин q_l и |q₂|, выраженных через т-ру и изменение энтропии на участках АВ и CD: h_t = 1-|q₂|/q_l = 1- Т₂|Ds_СD|/(T₁Ds_AB).Так как |Ds_CD|= Ds_AB , то h_tK= 1- T₂/T_I (3.6) Кпд цикла Карно зависит только от т-ры Т₁ источника и Т₂ приемника теплоты и не зависит от рода рабочего цикла. Этот вывод составляет содержание так называемойтеоремы Карно. Цикл Карно имеет наибольший термический кпдпо сравнению с другими циклами в интервале температур Т₁ - Т₂. Для док-ва этогоутверждения следует сравнить на sT-диаграмме (рис. 3.3) цикл Карно ABCD с произвольным циклом abcd, проходящим между теми же температурными границами. Для цикла Карно h_tК = 1-|q_2К|/q_lK. Из диаграммы видно, что q_2K = пл.еDС', а q_1K = пл.еАВf. Соответствен­но для произвольного цикла h_t = 1-|q₂|/q_l , где q₂ = пл.еаdсf, а q₁ = пл.еаbсf. Сравнивая соответствующие площади, замечаем, что q_2K<q₂,а q_1K> q_l. Отсюда q_2K/q_IK<q₂/q_l.Сл-но, h_tK> h_t. Эффективность превращения теплоты в работу (термический кпд) в любом другом цикле не Мб больше, чем в цикле Карно, осуществляемом в том же интервале т-р.Фундаментальное знач полученного рез-та состоит в том, что он устанавливает предел кпд тепловых двигателей. Взяв частные производные от h_tKсоответственно по T₁и Т₂, можно получить выражения, показывающие влияние изменения температур T_Iи Т₂источников теп­лоты на кпд цикла Карно: . 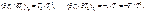Так как T_I>T₂, то, следовательно, 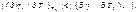Это значит, что измен т-ры Т₁, источника теплоты влияет на кпд меньше, чем изменение т-ры Т₂ приемника теплоты.Так как не существует ни источников теплоты с бесконечно высокой темпера­турой 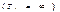, ни приемников теплоты с т-рой, равной абс 0 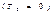, то отношение Т₂/Т_I всегда больше нуля. Сл-но, кпд цикла Карно и тем более любого другого цикла всегда мень 1.Кпд цикл Карно тем больше, чем меньше отношение T₂/T_I , т. е. чем ниже т-ра Т₂ и выше т-ра T_I. Хотя в наст вр технически возможно получение очень высоких т-р (сотни тысяч градусов), однако в реальных дви­гателях использовать эти т-ры невозможно, так как материалы, из кот изготовлены детали двигателей, не способны выдерживать такие т-ры. Мак­с практически реализуемая в большинстве авиадвигателей температура близка к 1000...2000 К. Имеются двигатели (например, ракетные), в которых используются более высокие температуры (до 4000 К). Однако эти двигатели рассчитаны на очень короткий срок службы.Т-ра Т₂ составляет приблизительно 300 К, поскольку приемником теплоты для всех двигателей, работающих в наземных условиях, является либо атмосферный воз­дух, либо вода в реках, морях и других водоемах. Может быть получена и темпе­ратура, близкая к абс 0, однако получение температур ниже т-ры окр ср связано с затратой работы. Затрата работы оказывается боль, чем выигрыш в кпд, поэтому такой путь увеличения кпд неприемлем.

45. Термические коэф хар-т тепловые и упругие св-ва тел. Известны коэф теплового расширения α , термический коэф давления β и изотермический коэфф сжимаемости γ.

При нагревании определенной массы в-ва при постоянном внешнем давлении изменение объема на каждый градус повышения т-ры выражается производной 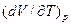. Относительное изменение объема при нагревании на один градус – коэффициент объемного расширения

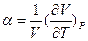
для идеального газа α=1/T.

Если нагревать данную массу в-ва при постоянном объеме, то относительное изменения давления при изменении т-ры харак-ся термическим коэф- давления β

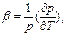, р- давление при Т. Для идеального газа β= α=1/Т.

При изотермическом сжатии данной массы в-ва отношение изменения объема при изменении давления на единицу давления к объему- изотермический коэффициент сжимаемости:

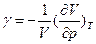, знак минус означает уменьшение объема с увеличением давления.

Ой З-н термод. для З Т С

2-й з-н термод. позволяет указать направление теплового потока и устанавливает максимально возможный предел превращения теплоты в работу в тепл.машинах.

а) Имеется подвод и отвод теплоты

Данное выражение явл. формулировкой 2 з. термод., энтропия увелич..

б) Воздействие в форме работы

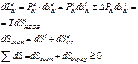
в) теплота+работа

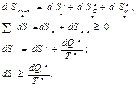
48. понятие об эксерги . эксерг-кий КПД. Эксергия количества теплоты. Экс.,та часть Е, кот. мож превратить в полезную работу (предельная величина). Виды эксергии: 1.Эксергия рабочего тела – тдля систем, включающих рабочее тело и окруж-ю среду. В этих сист исп-ся внутр.-я и внеш.-я энергия раб.тела. Различают эксергию покоящегося раб.тела и его потока.

2. Эксергию потока Е, включающую эксергию теплоты ( для систем, состоящих из источников теплоты, раб.тела и окруж.среды). Max-ное кол-во полезной работы, кот можно получить в цикле при заданных т-рах источников теплоты, назыв. работоспособностью (эксергией теплоты). Max-ную работу в тепл.двиг. мож получить по циклу Карно η_t=L_max/Q=1-T₂/T₁, Q- кол-во тепл. подведенное ;T₁ иT₂ – t-ры высшего и низшего источника теплоты; L_max – максимальное кол-тво работы, кот мож получить в обратимом цикле. L_max=E_max=Q₁(1-T₂/T₁)

(1-T₂/T₁) – коэфт эксерг-кой теплоты. E_max=q₁-T₂q₁/T₁. для получения полезной работы используется лишь часть некот кол-ва теплоты q₁, а часть “=” q=T₂q₁/T₁ рассеивается в окр.ср в реальном процессе добавляются потери, возникающие вследствие его необратимости. В необратимых процессах она уменьшается, превращаясь в анергию. Если энергия бесполезно рассеивается в окруж.среду, то вся эксергия превращается в анергию .

Эксергетический КПД определяется отношением исп-ой эксергии к подведенной.

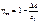
где Δе-разность подв. и отв. эксергий; е₁-подв. эксергия.

Эксерг. КПД позволяет учесть потери только из-за необратимости процесса, так как лишь в необратимых процессах происходит потеря эксергии, а для всех обратимых процессов η_е=1.

49.Физические величины, значения кот однозначно определяются состоянием системы и не зависят от ее предыстории, называютсяпараметрами состоянияили функциями состояния системы.

2 вида параметров состояния: координаты тд-ого состоянияи потенциалы вд-й.

Параметры состояния, обязательно изменяющиеся при наличии вд-я данного рода и не изменяющиеся под влиянием вд-я иных родов, наз координатами тд-ого состояния.

Потенциалом вд-янекот рода наз параметр состояния, различие значений кот между системой и окр ср на контрольной пов-ти приводит к возникновению вд-я данного рода, т.е. к передаче энергии в данной форме между системой и окружающей средой.

Ур-я, представляющие зав-ть параметров (функций) состояния равновесной сист от независимых параметров состояния, называютсяур состояния тд-ой системы.

Если обозначить произвольную функцию состояния системы через φ, а координаты состояния -- через x₁, x₂, …, x_n (п - число координат состояния, т. е. термодинамиче­ских степеней свободы), то уравнение состояния можно представить в виде : φ = φ (x₁, x₂, …, x_n ).

Тд-им процессомназывается изменение состояния тд-ой системы в рез-те ее вд-ия с окр ср.

Тд-ий процесс, протекающий с нарушением внутреннего равновесия в тд-ой системе, называетсянеравновесным

Тд-ий процесс, протекающий с бесконечно малым отклонением состояния системы от равновесного состояния, называетсяравновесным.

Эксергия З Т С.

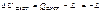
совершает работу за счет изм – я внутр.эн L_max=-ΔU_c/c=u^/ –и^//, u^/ – внутр.эн.сист в нач.состоянии, u^//- -/- в конечном сост.

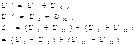
а) Т_о=const

б) P_o=const

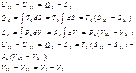
(сумма изменений обьема =0). Из усл – я получения Lmax принимаем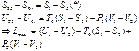

Равенство (*) справедливо только для обратимого взаимод-я,кот. опред-т L_мах.

Для получения самой величины экс. необх. положить конечн.сост. системы соот-ми параметрами окр.среды.

u₂ =u₀, s₂=s₀, v₂=v₀,

℮_{З Т С}=(U₁-U₀) – T₀(S₁-S₀) +P₀(V₁-V₀).

Чем > S₁ тем < работоспособ- ть сист.

Экс. внутр-й энергии – это часть (доля) вн.энергии, кот. в идеале превратима в полезную работу.

Δ℮_И=(U₁-U₂) – T₀(S₁-S₂) +P(V₁-V₂).

51. 2 зак является эмпирическим. Известно много различных формулировок, но его физичческая сущность наиболее четко расскрывается в формулировке, данной Больцманом.Он подчеркнул сво-во природы стремиться из состояний менее вероятных к более вероятным. Для ТД системы наиболее вероятным яв-ся состояние ТД равновесия. Если ТД систему вывести из равновесия, то за счет естественных процессов теплообмена сист прийдет к состоянию ТД равновесия. На этом факте основывается формулировка Клаузиса : теплота сама собой переходит лишь от тела с более высокой и не может самопроизвольно переходить обратно. Сл-но, равновесие мож нарушиться т-ко от внешнего воздействия окр. ср. 2 закон ТД, определя.щий условия протекания процессов в опр. направлении имеет чрезв. важное значение для обеспечения эффект. работы машин.

Энтропияизолированной сист им макс в стостоянии равновесия, когда в сист нет разностей температур и становятся невозможными самопроизвольные процессы. Это свойство энтропии изолированной системы можно рассматривать как одну из формулировок 2 закона ТД: энтропия всякой изолированной системы стремиться к максимуму.

52. Энерг.хар-ки термод. с/с – мы и внеш. возд-вии на нее.

Терм. сист. – объект, кот.выбирает терм-ка – это совок-ть макротел, отдельное макротело или его часть. Энерг.хар-ки: Е (внутр.эн.). Е явл мерой различных форм движения материи. Полная Е макросистемы: E=E_кин + Е_пот +U, где U – внутр.эн. Внутр.эн. – это Е заключенная в с/с. Она состоит из:

1) кинетич.Е поступательного, вращат. и колебат.движения молекул.

2) потенциал.Е.взаимод- вия молекул м/у собой (силы притяжения и отталкивания ). Свойства внутр.эн.

U=f(T,ν) U=f(P,T) U=f(P,ν) U – функция состояния 1) ΔU= U₂ – U₁, т.е.не зависит от пути

перехода

2) 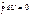свойство полного диф –ла :

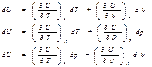
3) для ид.газа : U=f(T)

4)свойство аддетивности: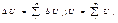

т.е.для сложной с/с внутр.эн.есть сумма внутр.Е, составляющих частей этой с/с ΔU > 0, если U₂ > U₁. Энерг.внеш.возд–вие:

1) тепловое возд. – передача Е за счет хаотич –го неупор – го движ –я частиц. Такая передача Е происходит м/у телами, имеюш –ми различ-ю t-ру , либо м/у телами на расст –ии посредством эл.магн.волн. Передача Е происходит от более нагретых тел к менее нагретым. Кол – во Е при такой передаче наз.кол –вом теплоты.

2) Работа – передача Е за счет строго упоряд – го движ – я частиц. В этом сл –е передача Е происходит при перемещении всего тела или его части в простр –ве. Возд – вий в виде работы очень много. L_магн, L_вращ, L_мех и др., [Дж]. Работа, затраченная телом ‘+’, а совершенная телом ‘-’ . Ур возд – вия: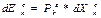

Р_к – силы (потенциалы), кот.связаны с внеш.возд. Х_к – коор –та, предт – ет собой конкр.- й пар –р, кот.изменяет- ся соот – но этому виду возд – вия. Р_к – причины возник – я внеш.- х возл- вий. Возд – вия возникают тогда, когда есть разность сил. ΔР_к= Р^е_к – Рⁱ_к , Х^е_к – следствие возд –.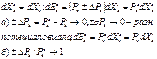

сильное неравномерное возд.→ в с/с протекаеют неравн –е процессы. 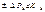- хар.степень нерав –ти.

к=2

- термодиф – формация с/с (м.б.откр.и закрытой) Число независимых пар – ров с/с (степеней свободы)= числу внеш. энерг- ких возд –вий.