Законы вращательного движения твердого тела
Кинематика, динамика, законы сохранения энергии
И импульса материальной точки. Элементы теории поля
Основные формулы
Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x
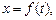
где f(t) - некоторая функция времени.
Проекция средней скорости на ось x
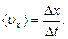
Средняя путевая скорость
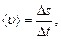
где Ds - путь, пройденный точкой за интервал времени Dt. Путь Ds в отличие от разности координат Dx = x2-x1не может убывать и принимать отрицательные значения, т.е. Ds ³ 0.
Проекция мгновенной скорости на ось x
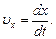
Проекция среднего ускорения на ось x
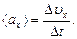
Проекция мгновенного ускорения на ось x
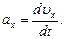
Кинематическое уравнение движения материальной точки по окружности
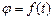 , r=R-const
, r=R-const
Модуль угловой скорости
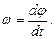
Модуль углового ускорения
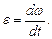
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

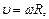
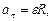
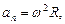
где 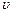 -модуль линейной скорости;
-модуль линейной скорости; 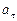 и
и 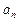 - модули тангенциального и нормального ускорений; w - модуль угловой скорости; e - модуль углового ускорения; R -радиус окружности.
- модули тангенциального и нормального ускорений; w - модуль угловой скорости; e - модуль углового ускорения; R -радиус окружности.
Модуль полного ускорения
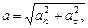 или
или 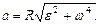
Угол между полным 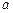 и нормальным
и нормальным 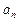 ускорениями
ускорениями
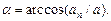
Импульс материальной точки массой m, движущейся со скоростью 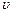 ,
,
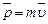 .
.
Второй закон Ньютона
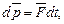
где 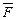 - результирующая сила, действующая на материальную точку.
- результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости
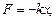
где 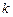 -коэффициент упругости (в случае пружины - жесткость);
-коэффициент упругости (в случае пружины - жесткость);
x - абсолютная деформация;
б) сила тяжести
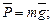
в) сила гравитационного взаимодействия
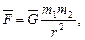
где 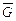 - гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность
- гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность 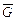 гравитационного поля:
гравитационного поля:
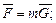
г) сила трения (скольжения)
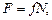
где f - коэффициент трения; N - сила нормального давления.
Закон сохранения импульса
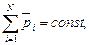
или для двух тел (i=2)
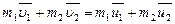 ,
,
где 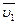 и
и 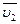 - скорости тел в момент времени, принятый за начальный;
- скорости тел в момент времени, принятый за начальный; 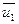 и
и 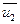 - скорости тех же тел в момент времени, принятый за конечный.
- скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно,
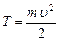 , или
, или 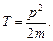
Потенциальная энергия:
а) упругодеформированной пружины
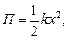
где 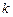 - жесткость пружины; x - абсолютная деформация;
- жесткость пружины; x - абсолютная деформация;
б) гравитационного взаимодействия
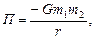
где 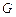 - гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
- гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в однородном поле силы тяжести,
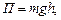
где g - ускорение свободного падения; h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где
R — радиус Земли).
Закон сохранения механической энергии
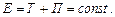
Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
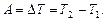
Примеры решения задач
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct3, где А = 2 м, В = 1 м/с, С = - 0,5 м/с3. Найти координату х, скорость 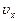 и ускорение
и ускорение 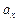 точки в момент времени t = 2с.
точки в момент времени t = 2с.
Решение. Координату xнайдем, подставив в уравнение движения числовые значения коэффициентов A, B и C и времени t:
x = (2 + 1×2 - 0,5×23)м = 0.
Мгновенная скорость относительно оси хесть первая производная от координаты по времени:
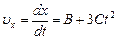 .
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
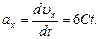
В момент времени t = 2 с
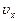 = (1 - 3×0,5×22) м/c = - 5 м/c;
= (1 - 3×0,5×22) м/c = - 5 м/c;
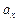 = 6(- 0,5) × 2 м/с2 = - 6 м/с2.
= 6(- 0,5) × 2 м/с2 = - 6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону j = A + Bt + Ct2, где A= 10 рад, В = 20 рад/с, С = - 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии г=0,1 м от оси вращения, для момента времени t =4 с.
Решение. Полное ускорение 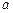 точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 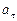 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 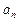 , направленного к центру кривизны траектории (рис.1):
, направленного к центру кривизны траектории (рис.1):
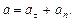
Так как векторы 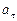 и
и 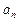 взаимно перпендикулярны, то модуль ускорения
взаимно перпендикулярны, то модуль ускорения
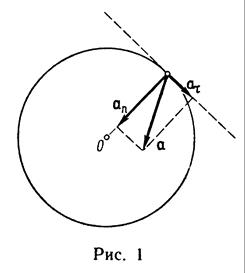
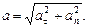
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
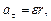
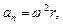
где w - модуль угловой скорости тела; e - модуль его углового ускорения.
Подставляя выражения 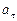 и
и 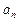 в формулу (1), находим
в формулу (1), находим
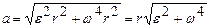 . (2)
. (2)
Угловую скорость w найдем, взяв первую производную угла поворота по времени:
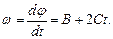
В момент времени t = 4 с модуль угловой скорости
w = [20 + 2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
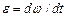 = 2 C = - 4 рад/с2.
= 2 C = - 4 рад/с2.
Подставляя значения w, e и r в формулу (2), получаем
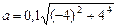 м/с = 1,65 м/с2.
м/с = 1,65 м/с2.
Пример 3. Шар массой m1, движущийся горизонтально с некоторой скоростью 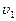 , столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
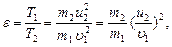 (1)
(1)
где Т1 - кинетическая энергия первого шара до удара; u2 и Т2 - скорость и кинетическая энергия второго шара после удара.
Как видно из формулы (1), для определения e надо найти u2. Согласно условию задачи импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем:
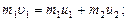 (2)
(2)

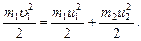 (3)
(3)
Решим совместно уравнения (2) и (3):
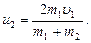
Подставив это выражение u2 в формулу (1) и сократив на u1 и m1, получим
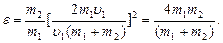
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
Пример 4. Через блок в виде сплошного диска, имеющего массу m= 80г (рис.2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 = 100г и m2 = 200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
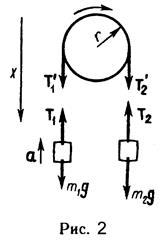 Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
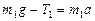 ; (1)
; (1)
для второго груза
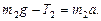 (2)
(2)
Под действием моментов сил 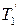 и
и 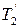 относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,
относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,
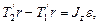 (3)
(3)
где 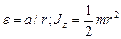 - момент инерции блока (сплошного диска) относительно оси z.
- момент инерции блока (сплошного диска) относительно оси z.
Согласно третьему закону Ньютона, с учетом невесомости нити 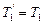 и
и 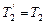 . Воспользовавшись этим подставим в уравнение (3) вместо
. Воспользовавшись этим подставим в уравнение (3) вместо 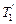 и
и 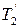 выражения
выражения 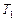 и
и 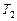 , получив их предварительно из уравнений (1) и (2):
, получив их предварительно из уравнений (1) и (2):
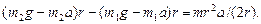
После сокращения на 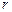 и перегруппировки членов найдем
и перегруппировки членов найдем
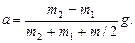 (4)
(4)
Формула (4) позволяет массы m1, m2 и m выразить в граммах, как они даны в условии задачи, а ускорение - в единицах СИ. После подстановки числовых значений в формулу (4) получим
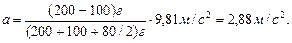
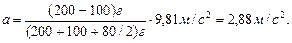
Пример 5. Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости u1, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R=6,37×106 м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли,пренебречь.
Решение. Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно,
Т1 + П1 = Т2 + П2, (1)
где Т1, П1 и Т2, П2 - кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях.
Согласно определению кинетической энергии,
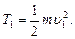
Потенциальная энергия ракеты в начальном состоянии
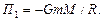
По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая - убывает. В конечном состоянии кинетическая энергия Т2 станет равной нулю, а потенциальная - достигнет максимального значения:
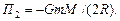
Подставляя выражения Т1, П1, Т2 и П2 в (1), получаем
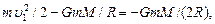
откуда
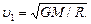
Заметив, что GM/R2=g (g - ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде
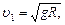
что совпадает с выражением для первой космической скорости.
Произведем вычисления:
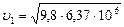 м/с = 7,9 км/с.
м/с = 7,9 км/с.
Таблица вариантов для задания № 1
| Вариант | Номер задач | ||||
101. Тело брошено вертикально вверх с начальной скоростью V0=4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью V0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
102. Материальная точка движется прямолинейно с ускорением а=5м/с2. Определить, на сколько путь, пройденный точкой в п-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять V0= 0.
103. Две автомашины движутся по дорогам, угол между которыми a=60°. Скорость автомашин V1=54 км/ч и V2=72км/ч. С какой скоростью V удаляются машины одна от другой?
104. Материальная точка движется прямолинейно с начальной скоростью V0=10 м/с и постоянным ускорением а=-5м/с2. Определить, во сколько раз путьΔs,пройденный материальной точкой, будет превышатьмодуль ее перемещения Δr спустя t=4c после начала отсчета времени.
105. Велосипедистехал из одного пункта в другой. Первую треть пути он проехал со скоростью V1=18 км/ч. Далее половину оставшегося времени он ехал со скоростью V2=22 км/ч, после чего до конечного пункта он шел пешком со скоростью V3=5км/ч. Определить среднюю скорость V велосипедиста.
106. Тело брошено под углом a = 30о к горизонту со скоростью vo = 30 м/с. Каковы будут нормальное an и тангенциальное at ускорения тела через время t = 1 с после начала движения.
107. Материальная точка движется по окружности с постоянной угловой скоростью w = p/6 рад/с. Во сколько раз путь Ds, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения Dr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол jо = p/3 рад.
108. Материальная точка движется в плоскости ху согласно уравнениям х = А1 + В1 t + С1 t2 и у = А2 + В2 t + С2 t2, где В1 = 7 м/с, С1 = - 2 м/с2, В2 = - 1 м/с, С2 = 0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t = 5 с.
109. По краю равномерно вращающейся с угловой скоростью w = 1 рад/с платформы идет человек и обходит платформу за время
t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
110.Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением e. Определить тангенциальное ускорение at точки, если известно, что за время t = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение
an = 2,7 м/с2.
111. При горизонтальном полете со скоростью V=250 м/с снаряд массой m=8кг разорвался на две части. Большая часть массой m1=6 кг получила скорость U1=400м/c в направлении полета снаряда. Определить модуль и направление скорости U2 меньшей части снаряда.
112. С тележки, свободно движущейся по горизонтальному пути со скоростью V1=3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной U1=4 м/с. Определить горизонтальную составляющую скорости U2x человека при прыжке относительно тележки. Масса тележки m1=210кг, масса человека m2=70 кг.
113. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a=30° к линии горизонта. Определить скорость U2 отката платформы, если снаряд вылетает со скоростью U1=480м/c. Масса платформы с орудием и снарядами m2=18т, масса снаряда m1=60 кг.
114. Человек массой m1=70 кг, бегущий со скоростью V1=9 км/ч, догоняет тележку массой m2=190кг, движущуюся со скоростью V2=3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
115. Конькобежец, стоя на коньках на льду, бросает камень массой m1=2,5 кг под углом a=30° к горизонту со скоростью V=10 м/с. Какова будет начальная скорость V0 движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
116. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1=60 кг, масса доски m2=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) V=1 м/с? Массой колес и трением пренебречь.
117. Снаряд, летевший со скоростью V = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью U1=150 м/с. Определить скорость U2 большего осколка.
118. Две одинаковые лодки массами m=200кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями V=1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1=200 кг. Определить скорости U1 и U2 лодок после перебрасывания грузов.
119. На сколько переместится относительно берега лодка длиной l=3,5м и массой m1=200 кг, если стоящий на корме человек массой m2=80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.
120. Лодка длиной 1=3 м и массой т=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами т1=60 кг и т2=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
121. В деревянный шар массой т1=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля массой т2= 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол a=3°? Размером шара пренебречь. Удар пули считать прямым, центральным.
122. По небольшому куску мягкого железа, лежащему на наковальне массой т1=300 кг, ударяет молот массой т2 = 8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
123. Шар массой m1=1 кг движется со скоростью V1= 4 м/с и сталкивается с шаром массой т2=2 кг, движущимся навстречу ему со скоростью V2=3 м/с. Каковы скорости и1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
124. Шар массой т1=3 кг движется со скоростью V1=2 м/с и сталкивается с покоящимся шаром массой т2 = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
125. Определить КПДh неупругого удара бойка массой т1=0,5 т, падающего на сваю массой т2=120 кг. Полезной считать энергию, затраченную на вбивание сваи.
126. Шар массой т1=4 кг движется со скоростью V1= 5 м/с и сталкивается с шаром массой m2 =6 кг, который движется ему навстречу со скоростью V2= 2 м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
127. Из ствола автоматического пистолета вылетела пуля массой m1 = 10 г со скоростью V = 300 м/с. Затвор пистолета массой m2 = 200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м.На какое расстояние отойдет затвор послевыстрела? Считать, что пистолет жестко закреплен.
128. Шар массой т1 = 5 кг движется со скоростью V1 = 1 м/с и сталкивается с покоящимся шаром массой т2 = 2 кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
129. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью V1 = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью V2 = 580 м/с. С какой скоростью откатилось при этом орудие?
130. Шар массой т1 = 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу т2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
131. Определить работу растяжения двух соединенных последовательно пружин жесткостями k1 = 400 Н/м и k2 = 250 Н/м, если первая пружина при этом растянулась на Dl = 2 см.
132. Из шахты глубиной h = 600 м поднимают клеть массой т1 = 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа A совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия h подъемного устройства?
133. Пружина жесткостью k = 500 Н/м сжата силой F = 100 H. Определить работу A внешней силы, дополнительно сжимающей пружину еще на Dl = 2 см.
134. Две пружины жесткостью k1 = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации Dl = 4 см.
135. Какую нужно совершить работу A, чтобы пружину жесткостью k = 800 Н/м, сжатую на х= 6 см, дополнительно сжать на Dx= 8 см?
136. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на Dl = 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
137. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость V пули при вылете ее из пистолета, если пружина была сжата на Dx = 4 см.
138. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью V = 0,6м/с, остановился, сжав пружину на Dl = 8 см. Найти общую жесткость k пружин буфера.
139. Цепь длиной l == 2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает '/зl, то цепь соскальзывает со стола. Определить скорость V цепи в момент ее отрыва от стола.
140. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3,0 м и внутренним диаметром d = 2,0 м? Плотность материала r принять равной 2,8×103 кг/м3.
141.Определить напряженность G гравитационного поля на высоте h = 1000 км над поверхностью Земли. Считать известными ускорение g свободного падения у поверхности Земли и ее радиус R.
142. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m = 2 кг:
1) с высоты h = 1000 км; 2) из бесконечности?
143. Из бесконечности на поверхность Земли падает метеорит массой m = 30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
144.С поверхности Земли вертикально вверх пущена ракета со скоростью v=5 км/с. На какую высоту она поднимется?
145.По круговой орбите вокруг Земли обращается спутник с периодом Т = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
146.На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
147.Спутник обращается вокруг Земли по круговой орбите на высоте h=520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
148. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h =1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
149.Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×108 м.
150.Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус Rз Земли в 390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
Расчетное задание № 2
Законы вращательного движения твердого тела.
