Умножение матрицы на число.

Произведением матрицы А на число a называется матрица 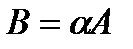, получаемая из А умножением всех ее элементов на число a:

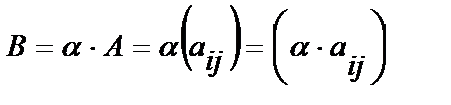
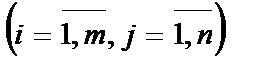
Например, .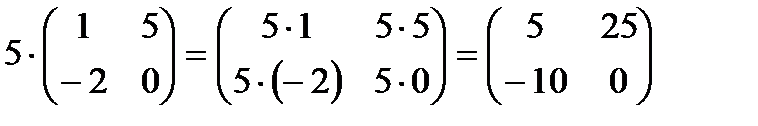

Произведение матрицы А на число 0 есть нулевая матрица, т.е. 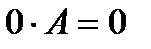. Матрица А не изменяется при умножении на единицу. Матрица (-1)А называется противоположной матрице А и обозначается –А.

Сложение матриц.

Суммой двух матриц А и В одинакового размера называется матрица С=А+В, элементы которой определяются равенством 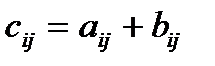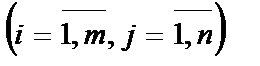(т.е. матрицы складываются поэлементно).

Например,

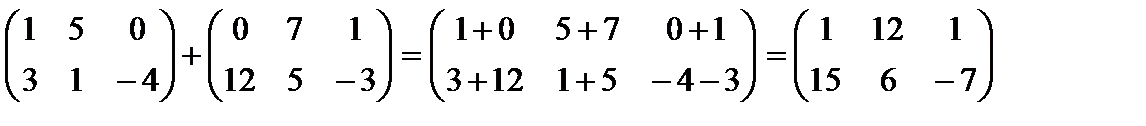
Линейные операции над матрицами обладают следующими свойствами:

1) А+В=В+А- коммутативность;

2) (А+В)+С=А+(В+С)- ассоциативность;

3) А+0=А;

4) А+(-А)=0;

5) a(A+B)=aА+aВ-дистрибутивность относительно матриц;

6) (a+β)A=aA+βA- дистрибутивность относительно чисел;

7) (aβ)А=a(βА)

Эти свойства справедливы для любых матриц А, В и С одинакового размера и любых a и β.

Произведение матриц.

Даны матрица А размером 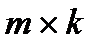и матрица В размером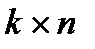

, .

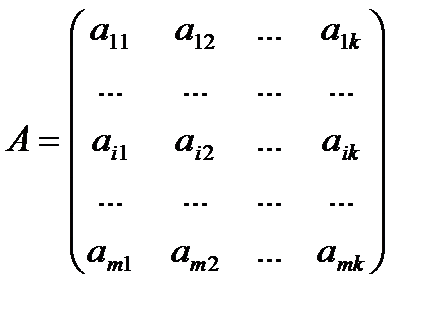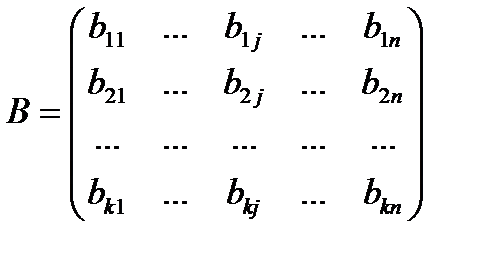Произведением матрицы А на матрицу В называется матрица 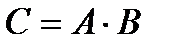, каждый элемент с_ij которой равен произведению i-ой строки матрицы А на j-ый столбец матрицы В. Умножение строки на столбец производится по формуле:

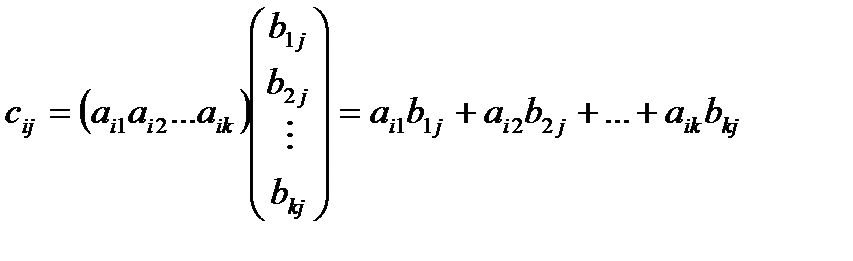
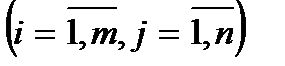
Отсюда видно, что умножать матрицу А на матрицу В можно только тогда, когда число столбцов матрицы А равно числу строк матрицы В. При этом матрица С=А·В будет иметь размер 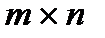, т.е. число строк m в ней равно числу строк первой матрицы в составе произведения А·В, а число столбцов n- числу столбцов второй матрицы. Это соотношение 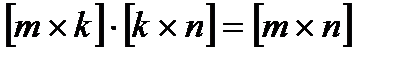называют правилом размерностей.

Пример. Пусть , .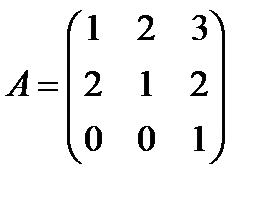

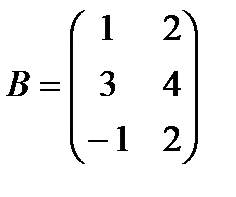Произведение А·В здесь существует, так как 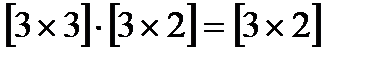, т.е. матрица А·В имеет размер .

.

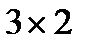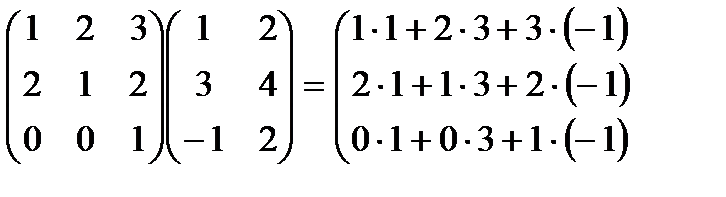
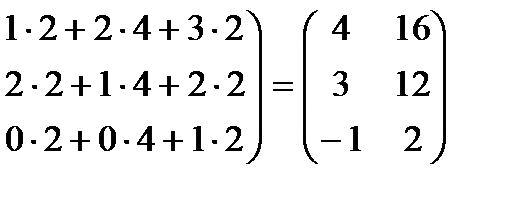Произведение В·А этих же матриц не определено, т.к. число столбцов матрицы В не равно числу строк матрицы А. Уже из приведенного примера следует, что произведение матриц не коммутативно, т.е. А·В¹В·А в общем случае.

Однако, даже если произведения А·В и В·А существуют, равенство А·В=В·А может не выполняться.

Справедливы следующие свойства:

1. (А·В)·С=А·(В·С)

2. А·(В+С)=А·В+А·С

3. (А+В)·С=А·С+В·С

4. a(А·В)=(aА)·В=А·(aВ)

Предполагается, что матрицы А, В и С здесь имеют нужные размеры.

Транспонирование матриц.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной. Матрицу, транспонированную относительно матрицы А, обозначим через А^т. Таким образом, если

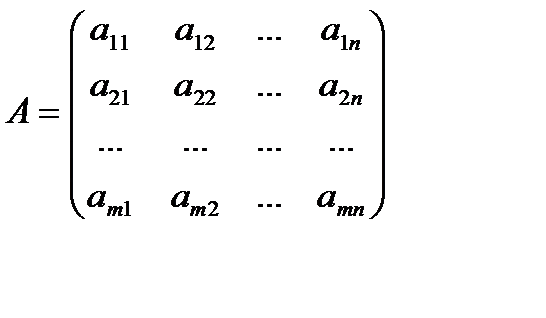, то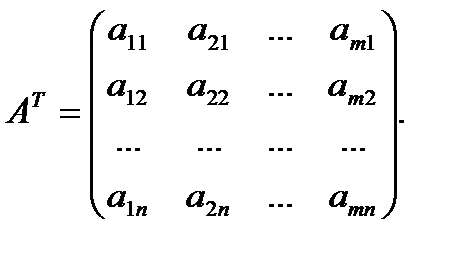

Отметим, что если А матрица размером 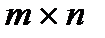, то матрица А^т имеет размеры 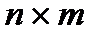. Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы. Справедливы следующие свойства:

1.

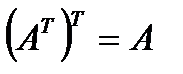
2.

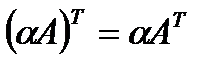
3.

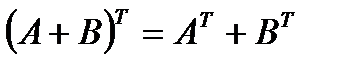
4.

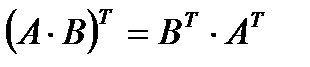
Определители.

Любой квадратной матрице А можно поставить в соответствие число, вычисляемое по определенному правилу и называемое определителем или детерминантом матрицы. В зависимости от порядка матрицы и определители называют соответственно определителями второго порядка, третьего порядка и т. д. Обозначают определители символами |А|, det А или

.

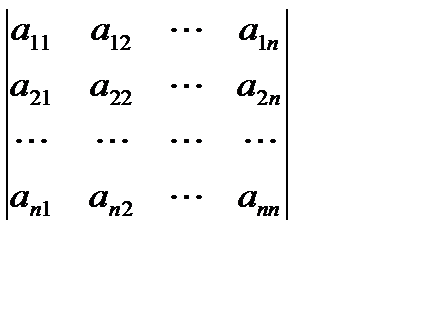Последняя запись является определителем n-го порядка, отвечающим матрице

.
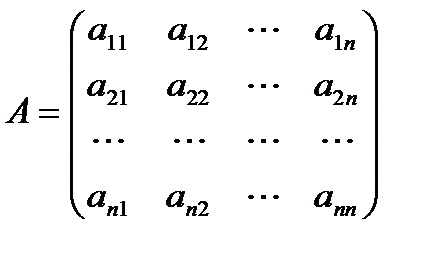