Плоскость и прямая в пространстве

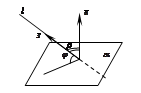1. Угол между прямой и плоскостью.

Опр. Углом между прямой и плоскостью называется меньший из двух смежных углов между прямой и ее проекцией на плоскость.

Таким образом, угол 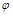между прямой 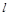и плоскостью 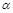принимает значения в промежутке .

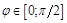Пусть прямая и плоскость заданы уравнениями:

, .

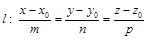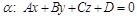Найдем угол между ними. Рассмотрим векторы

, . .

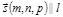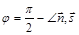
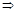
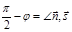
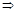
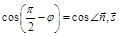
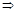
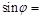
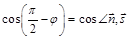
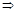
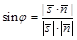Условие параллельности прямой и плоскости:

.

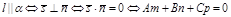Условие перпендикулярности прямой и плоскости:

.

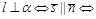
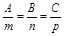Пересечение прямой и плоскости

Пусть заданы плоскость и прямая

, .

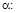
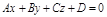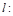
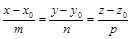Перейдем к параметрическим уравнениям прямой и подставим их в уравнение плоскости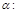

.

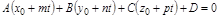1. Если 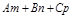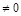, то находим значение t:

;

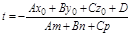подставляем его в уравнения прямой и находим координаты точки пересечения.

2. Если 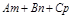=0, то 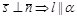, при этом:

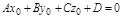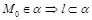а) если , то , т.е. прямая целиком лежит в плоскости;

б) если 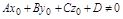, то 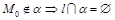, т.е. прямая параллельна плоскости и не имеет с ней общих точек.

ПР. Написать уравнения прямой 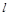, проходящей через точку 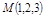перпендикулярно плоскости 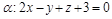. Найти точку пересечения 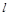и .

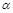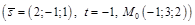
Поверхности

Опр. Пусть 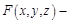некоторая функция, связывающая три переменные. Множество точек пространства, координаты которых удовлетворяют уравнению 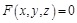, называется поверхностью в 3-мерном пространстве.

Если функция 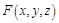линейная, то поверхность является плоскостью.

Цилиндрические поверхности

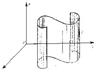Опр.Пусть L- некоторая линия в пространстве, через каждую точку которой проведены прямые, параллельные некоторой данной прямой l. Множество, являющееся объединением этих прямых, называется цилиндрической поверхностью или цилиндром; L − направляющаяцилиндра; прямые, параллельные l – образующие цилиндра.

Будем рассматривать уравнения поверхности в ДПСК.

Признак цилиндрической поверхности.

Если в уравнении поверхности отсутствует одна из координат, то эта поверхность – цилиндр с образующими, параллельными соответствующей координатной оси.

: .

: .

: .

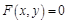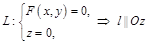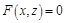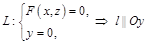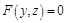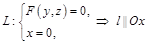Замечание. Название цилиндрической поверхности, как правило, дается по названию линии L.

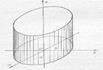
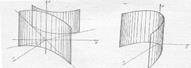
ПР. Построить поверхности:

а) 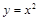, б) .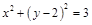

ПР. Построить тело: .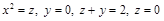

Поверхности второго порядка

Опр. Поверхностью 2-го порядка называется множество точек пространства, координаты которых удовлетворяют в ДПСК уравнению

,
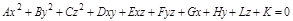где .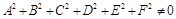

Будем считать, что в уравнении присутствуют все три координаты и коэффициенты 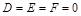. Тогда с помощью параллельного переноса системы координат уравнение можно привести к одному из следующих видов и получить следующие поверхности.

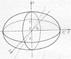
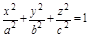− эллипсоид.

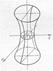
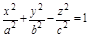− однополостный гиперболоид.

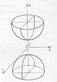
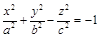− двуполостный гиперболоид.

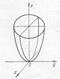
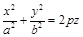− эллиптический параболоид.

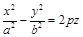− гиперболический параболоид.

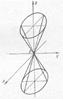
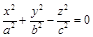− конус.