Системы управления с типовой структурой

На рис. 2.1 представлена модель СУ в форме “вход-выход”. Известен оператор w преобразования входного воздействия в выходной сигнал, заданный в одной из рассмотренных выше форм представления. Информация о внутренней организации в такой модели отсутствует (модель системы со свернутой организацией).

Рассмотрим модели с раскрытой внутренней организацией, которые отображают структуру СУ, то есть состав функциональных звеньев и связи между ними.

Многообразие объектов и СУ порождает и большое множество структур, отличающихся числом и составом звеньев и способов их взаимосвязей. Здесь ограничимся так называемой типовой структурой СУ, реализующей принцип обратной связи – см. подразд. 1.2, рис. 1.2, а также п. 1.3, рис. 1.7. К моделям такого вида может быть приведено описание значительного множества СУ различного функционального назначения.

Вариант типовой структуры СУ изображен на рис. 2.2.

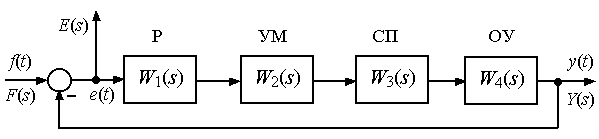
Рис. 2.2

Прямой канал образован объектом управления ОУ и рядом звеньев, обеспечивающих реализацию управляющего воздействия (в данном случае это - сервопривод СП и усилитель мощности УМ). Регулятор Р в соответствии с заложенным в него алгоритмом управления преобразует ошибку рассогласования в управляющее воздействие. В общем случае в зависимости от характеристик ОУ прямой канал может иметь разный состав последовательно соединенных функциональных звеньев.

Операторы звеньев СУ будем задавать передаточными функциями. ПФ прямого канала без обратной связи, то есть ПФ разомкнутой СУ, будем обозначать WР(s). ПФ последовательного соединения звеньев равна произведению ПФ отдельных звеньев, то есть

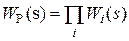. (2.19)

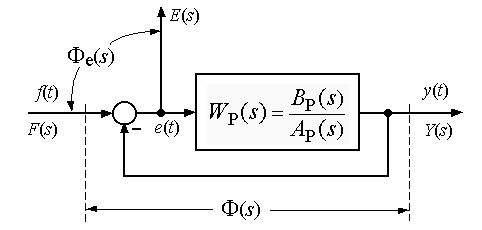
В результате типовая структура СУ может быть приведена к виду, представленному на рис. 2.3.

Рис. 2.3

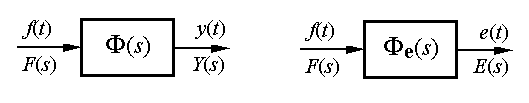В данной модели фигурируют три координаты: входное воздействие f(t), выходной управляемый сигнал y(t) и сигнал ошибки e(t). Этой модели можно поставить в соответствие две модели типа “вход-выход” - см. рис. 2.4.

а) б)

Рис. 2.4

На рис. 2.4,а представлена модель в виде ПФ Ф(s) замкнутой системы по управлению.

На рис. 2.4,б представлена модель в виде ПФ Фe(s) замкнутой системы по ошибке.

Связь ПФ замкнутой и разомкнутой типовой СУ. Характеристический полином типовой СУ

Для СУ с типовой структурой (см. рис. 2.3), выразим ПФ Ф(s) и Фe(s) замкнутой системы через оператор WР(s) прямой цепи, то есть системы без обратной связи.

ПФ по управлению

ПФ Ф(s) =Y(s) /F(s). Для получения этого оператора по модели, изображенной на рис. 2.3, необходимо исключить координату E(s):

Y(s) = E(s)WР(s) = (F(s)-Y(s))WР(s). (2.20)

Из (2.20) получаем

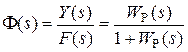. (2.21)

Выразим теперь ПФ замкнутой системы по управлению через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.21) WР(s) = BР(s) /AР(s), получим

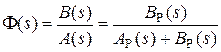. (2.22)

Таким образом, числители ПФ разомкнутой и ПФ по управлению замкнутой систем совпадают.

Знаменатель ПФ замкнутой системы A(s), он же - характеристический полином замкнутой системы, равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы.

ПФ по ошибке

ПФ Фe(s) =E(s) /F(s). Для получения этого оператора по модели, изображенной на рис. 2.3, необходимо исключить координату Y(s):

E(s) = F(s) -Y(s) = F(s) - E(s)WР(s) . (2.23)

Из этого соотношения получаем

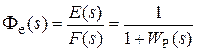. (2.24)

Выразим теперь ПФ замкнутой системы по ошибке через полином числителя и знаменателя ПФ разомкнутой системы. Подставляя в (2.24) WР(s) = BР(s) /AР(s), получим

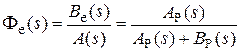. (2.25)

Таким образом, числитель ПФ замкнутой системы по ошибке совпал со знаменателем ПФ разомкнутой системы.

Знаменатель ПФ замкнутой системы A(s), он же - характеристический полином замкнутой системы, также равен сумме полиномов знаменателя и числителя ПФ разомкнутой системы.

Сразу обобщим важную особенность. У некоторой СУ - один характеристический полином; он не зависит от назначенных входа и выхода при получении конкретной ПФ.

Соотношения (2.21), (2.22) и (2.24), (2.25) справедливы для рассматриваемой здесь типовой СУ, то есть для одноконтурной системы с единичной отрицательной обратной связью.