Основные теоретические сведения и расчетные формулы
Рассмотрим такой вид нагружения, как растяжение (сжатие), при котором в поперечных сечениях бруса возникают только продольные силы, направленные вдоль его оси, все остальные внутренние усилия равны нулю.
Продольная, или нормальная сила, N считается положительной при растяжении и отрицательной при сжатии. Ее величина может быть найдена с помощью метода сечений: она численно равна алгебраической сумме проекций на ось бруса всех внешних сил, приложенных к брусу по одну сторону от рассматриваемого сечения.
Действующая в поперечном сечении продольная сила N равномерно распределяется по всему сечению и, как следствие этого, нормальные напряжения 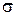 также равномерно распределяются по всему сечению.
также равномерно распределяются по всему сечению.
Их величина определяется по формуле
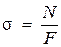 , (1.1)
, (1.1)
где N - продольная сила в поперечном сечении;
F - его площадь.
В системе СИ сила выражается в ньютонах, площадь поперечного сечения - в квадратных метрах (м2), нормальное напряжение - в паскалях (Па).
Сила может быть выражена в килограммах, а напряжение в килограммах, деленных на сантиметр в квадрате.
Абсолютное удлинение бруса при растяжении определяется по формуле
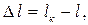 (1.2)
(1.2)
где l - начальная длина бруса;
lк - длина бруса после деформации.
Относительное удлинение бруса (относительная продольная деформация)
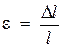 . (1.3)
. (1.3)
При растяжении Dl > 0 и e > 0, при сжатии эти величины отрицательны.
Абсолютное поперечное сужение
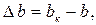 (1.4)
(1.4)
где b - первоначальный поперечный размер бруса;
bк - величина поперечного размера бруса после нагружения.
Относительное поперечное сужение (относительная поперечная деформация)
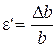 . (1.5)
. (1.5)
Абсолютная величина отношения 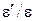 , обозначаемая
, обозначаемая 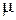 , называется коэффициентом Пуассона. Она является постоянной для каждого материала и характеризует его упругие свойства:
, называется коэффициентом Пуассона. Она является постоянной для каждого материала и характеризует его упругие свойства:
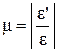 (1.6)
(1.6)
Между нормальным напряжением и относительным удлинением существует прямая пропорциональная зависимость, называемая законом Гука
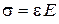 , (1.7)
, (1.7)
где E - коэффициент пропорциональности ( модуль упругости первого рода, или модуль Юнга).
Модуль упругости - это физическая характеристика материала, измеряемая в тех же единицах, что и нормальное напряжение.
Учитывая, что 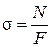 и
и 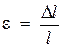 , можно записать выражение для вычисления абсолютного удлинения бруса в виде
, можно записать выражение для вычисления абсолютного удлинения бруса в виде
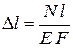 . (1.8)
. (1.8)
Для ступенчатого стержня и (или) стержня с несколькими продольными нагрузками удлинение подсчитывается как алгебраическая сумма удлинений участков бруса, в пределах которых N, E, F постоянны:
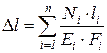 . (1.9)
. (1.9)
Если же величины N и F изменяются по длине бруса, его абсолютное удлинение вычисляется по формуле
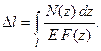 (1.10)
(1.10)
Используя соотношение smax £ [s], называемое условием прочности, можно решить три основных задачи сопротивления материалов.
1. Подобрать сечение растянутого (сжатого) бруса, при котором его прочность будет обеспечена. Расчетная формула в этом случае имеет вид
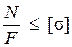 , (1.11)
, (1.11)
где N - продольная сила в опасном сечении бруса (сечении, в котором действует максимальное нормальное напряжение);
F - площадь поперечного сечения бруса;
[s] - допускаемое напряжение материала бруса.
Отсюда определяется необходимая площадь его сечения
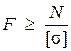 . (1.12)
. (1.12)
Зная форму сечения и его площадь, можно определить линейные размеры сечения или по сортаменту подобрать требуемый стандартный профиль: уголок, швеллер, двутавр и т. д.
Допускаемое напряжение [s] либо задается заранее, либо находится по формуле
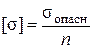 , (1.13)
, (1.13)
где sопасн = sт - предел текучести для пластичных материалов; sопасн= 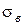 - временное сопротивление для хрупких материалов;
- временное сопротивление для хрупких материалов;
n - запас прочности материала .
2. Определить допускаемую нагрузку, если известны прочностные свойства материала и площадь поперечного сечения бруса.
Расчетная формула, вытекающая из условия прочности
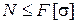 , (1.14)
, (1.14)
позволяет вычислить наибольшее значение продольной силы N, действующей в опасном сечении и, следовательно, величину внешних нагрузок, приложенных к брусу.
3. Проведение поверочного расчета прочности бруса.
При поверочном расчете нагрузки, размеры и материал, из которого изготовлен брус, считаются известными. Вычисляется наибольшее нормальное напряжение в опасном поперечном сечении и сравнивается с допускаемым:
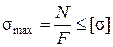 (1.15)
(1.15)
Если smax £ [s], то прочность бруса обеспечена.
