Основные правила дифференцирования
Правило 1. Производная постоянного числа равна нулю.
Это простейшее правило – оно следует и из определения; и из физического смысла – если путь не изменяется, то скорость равна нулю.
Правило 2. Производная суммы функций.
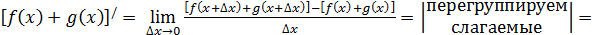
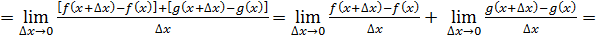
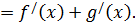
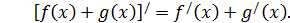
Кратко говорят: «производная суммы равна сумме производных».
Правило 3. Производная произведения функций.
Сначала заметим следующее: если 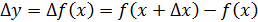 , то
, то 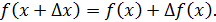 Поэтому:
Поэтому:
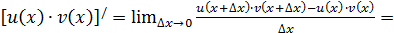
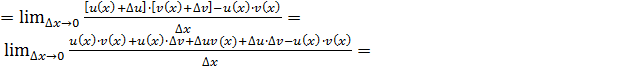
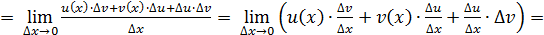
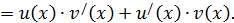 Мы учли, что
Мы учли, что 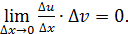
Итак, для запоминания короче: (u•v 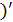 =
= 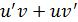 , - «производная произведения равна производной первого сомножителя, умноженной на неизменный второй плюс наоборот - производная второго сомножителя, умноженная на неизменный первый».
, - «производная произведения равна производной первого сомножителя, умноженной на неизменный второй плюс наоборот - производная второго сомножителя, умноженная на неизменный первый».
Следствие 1. Если 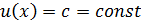 , то
, то 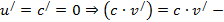
постоянный множитель можно выносить на знак производной,
Следствие 2. Поскольку в формуле сомножители равноправны, то она легко обобщается на случай любого числа сомножителей. Например, для четырёх сомножителей.
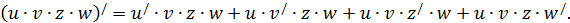
Правило 4.Производная дроби (частного двух функций).
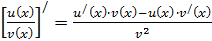 или короче для запоминания:
или короче для запоминания: 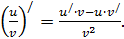
Формула доказывается аналогично.
Правило 5. Производная сложной функции.
Это правило является важнейшим - умение его применять наряду с отличным знанием таблицы производных и обеспечивает технику дифференцирования.
Определение. Пусть дана некоторая функция 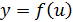 , где аргумент
, где аргумент 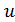 в свою очередь является функцией аргумента
в свою очередь является функцией аргумента 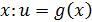 . По этой причине
. По этой причине 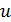 называется промежуточным аргументом. Тогда
называется промежуточным аргументом. Тогда 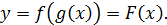 Функция
Функция 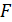 называется сложной функцией аргумента
называется сложной функцией аргумента 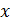 - сначала вычислим
- сначала вычислим 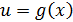 , а затем уже
, а затем уже 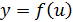 . Получается, что сложная функция
. Получается, что сложная функция 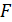 есть
есть 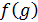 - «функция от функции».
- «функция от функции».
Например, 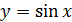 - простая функция, а функция
- простая функция, а функция 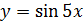 - сложная. Сложной функцией будет
- сложная. Сложной функцией будет 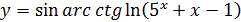 и т.д. Как видим, термин «сложная функция» не обязательно означает её громоздкость – это «функция от функции».
и т.д. Как видим, термин «сложная функция» не обязательно означает её громоздкость – это «функция от функции».
Итак, пусть 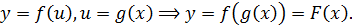 Предположим, что
Предположим, что 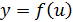 и
и 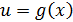 – функции, производные которых мы знаем (например, функции из таблицы производных). Вопрос: как найти производную
– функции, производные которых мы знаем (например, функции из таблицы производных). Вопрос: как найти производную 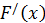 ?
?
Пример 3. 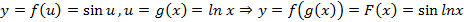 .
.
Здесь мы по таблице производных знаем: 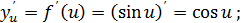
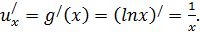 Вопрос: как найти
Вопрос: как найти 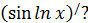
 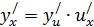 |
Формула производной сложной функции имеет простой вид:
производная сложной функции равна произведению простых функций, её составляющих.
Легко обобщить её на случай более громоздкой сложности: например, пусть 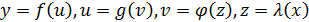 , т.е.
, т.е. 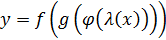 , тогда
, тогда
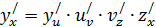 |
Пример 4. Найти производную функции 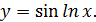
Решение. Это сложная функция: 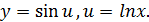 Из таблицы:
Из таблицы: 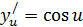 ,
, 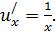
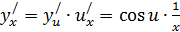 - подставим
- подставим 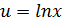 и получаем:
и получаем: 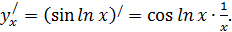
Конечно, каждый раз сложную функцию расчленять на простые - занятие обременительное. На практике делается следующим образом.
Пример 5. Найти производную функции 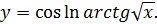
Решение. Смотрим на данную функцию и говорим: во-первых, это косинус аргумента 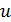 (что собой представляет аргумент
(что собой представляет аргумент 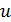 мы не записываем, а просто его видим:
мы не записываем, а просто его видим: 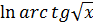 ). Вспоминаем таблицу производных:
). Вспоминаем таблицу производных: 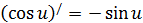 и записываем (помня чему равен промежуточный аргумент
и записываем (помня чему равен промежуточный аргумент 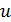 ):
): 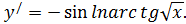 Но на этом моменте мы не останавливаемся – ведь производная
Но на этом моменте мы не останавливаемся – ведь производная 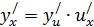 . Мы только записали первый сомножитель и ещё нужно найти
. Мы только записали первый сомножитель и ещё нужно найти 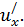 Поэтому, мы должны были написать
Поэтому, мы должны были написать
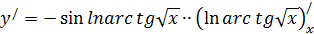 .
.
Далее требуется найти аналогично производную «укороченной» функции 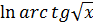 по тому же алгоритму. Поскольку алгоритм один и тот же, рассуждаем аналогично: перед нами функция
по тому же алгоритму. Поскольку алгоритм один и тот же, рассуждаем аналогично: перед нами функция 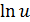 (промежуточный аргумент
(промежуточный аргумент 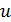 теперь равен
теперь равен 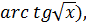 производная равна
производная равна 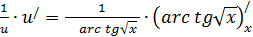 и так далее, пока не дойдём до окончательного, независимого, аргумента
и так далее, пока не дойдём до окончательного, независимого, аргумента 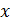 :
:
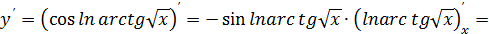
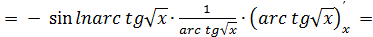
= 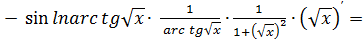
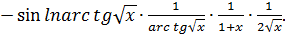
Или с подробными объяснениями:
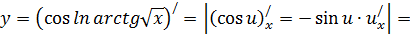
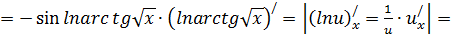
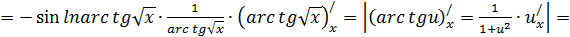
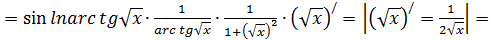
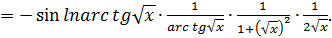
Читатель видит, что если всё делать подробно, то приходится одно и то же переписывать несколько раз. Это не рационально. Поэтому все промежуточные выкладки, которые мы заключили в скобки, держим «в уме», результат записываем сразу весь без повторений:
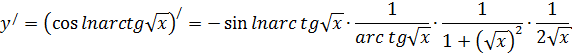
Нетрудно понять, что как бы громоздка ни была функция, её дифференцирование не представляет труда – ведь на каждом следующем применении формулы производной сложной функции, функция «укорачивается».
