Арифметическая и геометрическая прогрессии

Определение: Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией. Обозначение: a_1,. a₂ a_3, a_4,…..,a_n.

Из определения арифметической прогрессии следует, что разность между любым ее членом и ему предшествующим равна одному и тому же числу, т.е. a₂-a₁=a₃-a₂=...=а_k–a_k-1. Это число называется разностью арифметической прогрессии и обозначается буквой d.

Для того чтобы задать арифметическую прогрессию (а_п), достаточно знать ее первый член a₁и разность d. Если разность арифметической прогрессии — положительное число, то такая прогрессия является возрастающей; если отрицательное число, то убывающей. Если разность арифметической прогрессии равна нулю, то все ее члены равны между собой и прогрессия является постоянной последовательностью.

Формула n-го члена арифметической прогрессии имеет вид:

a_n = a₁ + d(n— 1)

Формула суммы ппервых членов арифметической прогрессии имеет вид:

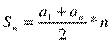или

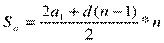
Определение:: Числовая последовательность, первый член которой отли­чен от нуля, а каждый член, начиная со второго, равен пред­шествующему члену, умноженному на одно и то же не равное нулю число, называется геометрической прогрессией.

Из определения геометрической прогрессии следует, что от­ношение любого ее члена к предшествующему равно одному и тому же числу, т.е. 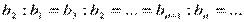. Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.

Для того чтобы задать геометрическую прогрессию (b_п), достаточно знать ее первый член b₁ и знаменатель q.

Если q>0 (q≠1), то прогрессия является монотонной последовательностью. Пусть, например, b₁= - 2, q = 3, тогда гео­метрическая прогрессия -2, -6, -18,... есть монотонно убываю­щая последовательность.

Если q=1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последователь­ностью.

Формула n-го члена геометрической прогрессии имеет вид:

b_n = b_1* q

Формула суммы ппервых членов геометрической прогрессии имеет вид:

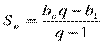или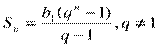

^
Прогресии

Уровень А

№45

а) Найдите разность арифметической прогрессии, первый член которой равен -21, а двенадцатый равен 1.

б) Найдите разность арифметической прогрессии, первый член которой равен -37, а двадцатый равен 1.

№46

а) Найдите седьмой член арифметической прогрес­сии, разность которой равна ее восьмому члену.

б) Найдите девятый член арифметической прогрессии, разность которой равна ее десятому члену.

№47

а) Найдите сумму первых восьми членов арифмети­ческой прогрессии, первый член которой равен -12, а второй равен -9.

б) Найдите сумму первых шести членов арифметиче­ской прогрессии, первый член которой равен -16, а второй равен -12.

№48

а) Найдите двенадцатый член арифметической прогрессии, если ее одиннадцатый член равен 15, а десятый член равен

б) Найдите семнадцатый член арифметической прогрессии, если ее восемнадцатый член равен 25. а девятнадцатый член равен 39.

№49

а) Сумма седьмого и двенадцатого членов арифмети­ческой прогрессии меньше суммы ее шестого и один­надцатого членов на 8. Найдите разность прогрессии.

б) Сумма шестого и десятого членов арифметической прогрессии меньше суммы ее третьего и восьмого чле­нов на 15. Найдите разность прогрессии.

Уровень В

№50

а) Первый член арифметической прогрессии равен 1, а разность прогрессии равна 7. Какие из чисел 28, 55, 9150 являются членами этой прогрессии?

б) Первый член арифметической прогрессии равен 1, а разность прогрессии равна 3. Какие из чисел 27, 68, 4276 являются членами этой прогрессии?

№51

а) В арифметической прогрессии седьмой член равен -40, а семнадцатый равен -50. Найдите разность этой арифметической прогрессии.

б) В арифметической прогрессии восьмой член ра­вен -22, а двадцатый равен -58. Найдите разность этой арифметической прогрессии.

№52

а) В арифметической прогрессии второй член равен 4, а двадцать восьмой равен 56. Найдите разность этой прогрессии и сумму 28 первых ее членов.

б) В арифметической прогрессии второй член ра­вен 10, а тридцать второй равен 130. Найдите раз­ность этой прогрессии и сумму 32 первых ее членов.

№53

а) В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой про­грессии и сумму первых десяти ее членов.

б) В арифметической прогрессии второй член ра­вен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.

№54

а) В арифметической прогрессии второй член равен 7, а сумма 22 первых членов равна 2035. Найдите пер­вый член и разность этой прогрессии.

б) В арифметической прогрессии второй член равен 3, а сумма 18 первых членов равна 1539. Найдите пер­вый член и разность этой прогрессии.

Уровень С

№55

а) В арифметической прогрессии второй член равен 10, разность равна 3, а сумма первых n членов прогрессии равна 282. Найдите n.

б) В арифметической прогрессии второй член равен 5, разность равна 3, а сумма первых n членов прогрессии равна 222. Найдите n.

№56

а) Найдите сумму всех членов арифметической про­грессии 2; 6; ... с седьмого по тринадцатый включи­тельно.

б) Найдите сумму всех членов арифметической прогрессии 8; 6; ... с шестого по двенадцатый включи­тельно.

№57

а) Найдите разность четырнадцатого и одиннадцато­го членов геометрической прогрессии, если их сумма равна 28, а произведение третьего и двадцать второго членов этой прогрессии равно 75.

б) Найдите разность восьмого и шестого членов гео­метрической прогрессии, если их сумма равна 16, а произведение второго и двенадцатого членов этой прогрессии равно 28.

№58

а) Найдите шестой и десятый члены геометрической прогрессии, если их сумма равна 16, а произведение четырнадцатого и второго членов этой прогрессии равно 60.

б) Найдите седьмой и четырнадцатый члены геометрической прогрессии, если их сумма равна 21, а произведение десятого и одиннадцатого членов этой про­грессии равно 98.

№59

а) Найдите знаменатель геометрической прогрессии, если разность ее шестнадцатого и тринадцатого чле­нов в 12 раз больше суммы двенадцатого, тринадца­того и четырнадцатого членов.

б) Найдите знаменатель геометрической прогрессии, если разность ее тридцатого и двадцать седьмого чле­нов в 30 раз больше суммы двадцать шестого, два­дцать седьмого и двадцать восьмого членов.

№60

а) Между первым и вторым членами арифметической прогрессии, разность которой равна 42, поместили 5 чисел так, что эти 7 чисел стали последовательными! членами новой арифметической прогрессии. Найдите разность этой новой прогрессии.

б) Между первым и вторым членами арифметической прогрессии, разность которой равна 36, поместили 11 чисел так, что эти 13 чисел стали последовательными членами новой арифметической прогрессии. Найдите разность этой новой прогрессии.

№61

а) Найдите разность арифметической прогрессии, в которой первый член равен 66, а произведение второго и двенадцатого членов является наименьшим из возможных.

б) Найдите разность арифметической прогрессии, в которой первый член равен 28, а произведение второго и восьмого членов является наименьшим из возможных.

Уровень D

№62

а) Найдите первый член и знаменатель геометрической прогрессии, в которой сумма квадрата девятого члена и восемнадцатого члена в 13 раз больше семна­дцатого члена, а разность квадрата седьмого члена и четырнадцатого члена в 7 раз больше тринадцатого члена.

б) Найдите первый член и знаменатель геометриче­ской прогрессии, в которой сумма квадрата седьмого члена и четырнадцатого члена в 18 раз больше три­надцатого члена, а разность квадрата девятого члена и восемнадцатого члена в 8 раз больше семнадцатого члена.

№63

а) Найдите произведение двенадцатого, семнадцато­го, двадцать второго и двадцать седьмого членов гео­метрической прогрессии, если известно, что произве­дение десятого и двадцать девятого ее членов рав­но 22.

б) Найдите произведение одиннадцатого, двадцатого, двадцать девятого и тридцать восьмого членов гео­метрической прогрессии, если известно, что произве­дение восемнадцатого и тридцать первого ее членов равно 29.

№64

а) Сумма четырнадцатого и второго членов геомет­рической прогрессии равна 16, а сумма их квадратов равна 200. Найдите восьмой член прогрессии.

б) Сумма одиннадцатого и третьего членов геомет­рической прогрессии равна 14, а сумма их квадратов равна 130. Найдите седьмой член прогрессии.