ПОЗИЦИОННЫЕ ЗАДАЧИ. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ. Решение задачи на построение точек пересечения прямой с поверхностью аналогично

С ПОВЕРХНОСТЬЮ

Решение задачи на построение точек пересечения прямой с поверхностью аналогично решению задачи на определение точки пересечения прямой с плоскостью.

В общем случае указанная задача решается следующим образом. На поверхности отмечают линию, которая лежит в одной проецирующей плоскости с заданной прямой. Точки пересечения этих двух линий являются искомыми точками пересечения.

Одной проекцией, отмеченной на поверхности линии, является отрезок прямой, принадлежащей одноименной проекции заданной прямой. Другая её проекция может быть построена исходя из принадлежности линии поверхности. Если при этом она имеет простую форму (многоугольник, окружность), то задача решается непосредственно на исходных проекциях. В других случаях для упрощения решения задачи будет целесообразно построить дополнительную проекцию этой линии и прямой.

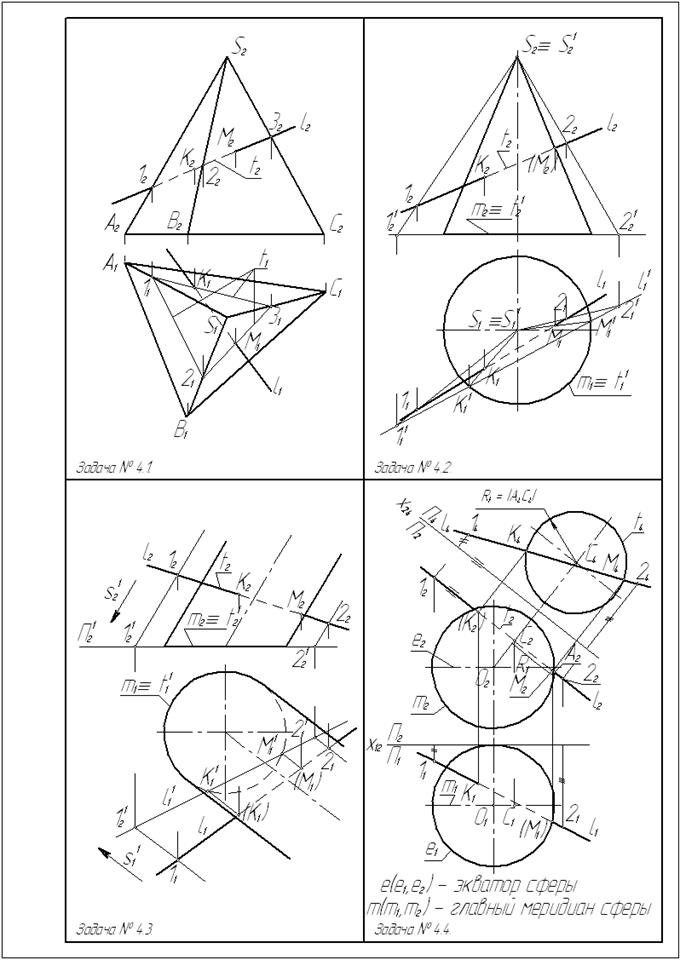
Задача № 4.1. Построить точки К и М пересечения прямой l c поверхностью трехгранной пирамиды SABC.

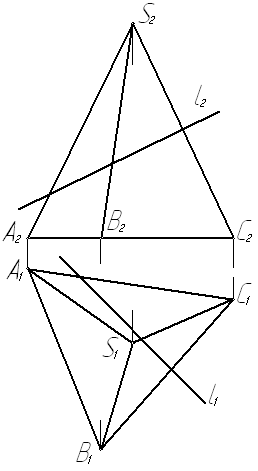
Рис. 21

Отметим на поверхности пирамиды линию t(D1-2-3), фронтальная проекция t₂

которой частично совпадает с фронтальной проекцией l₂ заданной прямой l (в пространстве прямая l и линия t принадлежат одной фронтально проецирующей плоскости). Линия t представляет собой замкнутую трехзвенную ломаную линию, сторонами которой являются отрезки прямых 1-2, 2-3, 3-1, расположенные в соответствующих гранях пирамиды. Точки К и М пересечения прямой l с линией t - искомые точки пересечения прямой l с поверхностью пирамиды SABC. Сначала находим горизонтальные проекции К₁, М₁ этих точек в пересечении горизонтальных проекций l₁ и t₁, а затем их фронтальные проекции К₂,М₂ на фронтальной проекции l₂ прямой l.

Определим видимость прямой l.

Относительно плоскости П₁ все три боковые грани видимы, значит видимы обе точки К и М пересечения прямой l с поверхностью пирамиды. Относительно плоскости П₂ грани SAB и SBC видимы, а грань SAC невидима. Следовательно, участок прямой l левее точки К невидим, а правее точки М видим.

Задача № 4.2. Построить точки К и М пересечения прямойl с конической поверхностью.

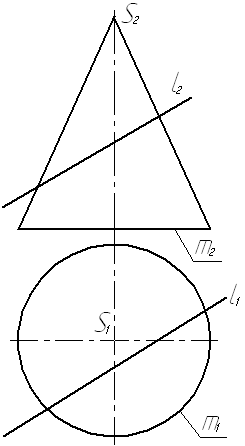
Рис. 22

Выделим на конической поверхности линию t, у которой t₂ Ì l₂ (линии t и l принадлежат данной фронтально проецирующей плоскости). Линия t представляет собой эллипс. Эллипсом будет и её горизонтальная проекция t₁. Чтобы избежать построения эллипса t₁, спроецируем кривую t и прямую l из вершины конической поверхности S¢º S на плоскость П¢É m. При этом линия t проецируется в кривую t¢º m, а прямая l - в прямую l¢ ( прямая l¢ определена дополнительными проекциями 1¢ и 2¢ точек 1 и 2 прямой l).

Точки К¢ и М¢ пересечения кривой линии t¢ с прямой l¢ являются дополнительными центральными проекциями искомых точек. Точки К и М получены на прямой l при помощи обратного проецирования точек К¢ и М¢.

Для определения видимости прямой достаточно, как и в предыдущей задаче, установить видимость точек её пересечения с поверхностью. Видимость последних определена по видимости проходящих через них образующих поверхности.

Задача № 4.3. Построить точки К и М пересечения прямой l с поверхностью цилиндра.

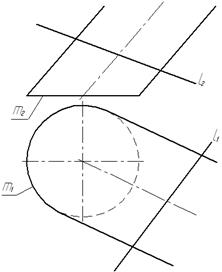
Рис. 23

Построение точек пересечения прямой l с поверхностью цилиндра аналогично построению точек пересечения прямой с поверхностью конуса с той лишь разницей, что дополнительное проецирование в данном случае параллельное. Направление проецирования s¢ параллельно образующим цилиндра, а плоскость дополнительных проекций П¢ проходит через линию основания цилиндра m.

Задача № 4.4. Построить точки К и М пересечения прямой l со сферой.

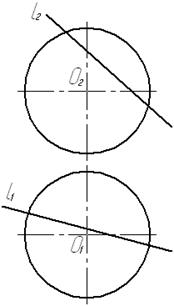
Рис. 24

Для построения точек пересечения прямой l со сферой на последней отмечена окружность t с центром в точке С, фронтальная проекция t₂ которой частично совпадает с фронтальной проекцией l₂ прямой l (l и t лежат в одной фронтально проецирующей плоскости). Чтобы не строить эллипс, в который окружность t проецируется на плоскость П₁, построена дополнительная ортогональная проекция прямой l и окружности t на плоскости П₄, параллельной плоскости, которой принадлежат окружность t и прямая l, и перпендикулярной к плоскости проекций П₂. При этом ось Х₂₄ параллельна t₂Ì l₂. На плоскости проекций П₄ заданная прямая l проецируется в прямую l₄, а окружность t – в окружность t₄, радиус R которой равен длине отрезка А₂С₂, а центр С₄ строится из условия принадлежности точки С главному меридиану m сферы. Отметим точки К₄ и М₄ пересечения дополнительных проекций t₄ и l₄ окружности t и прямой l и, проводя линии связи, определяем на l₂ и l₁ проекции искомых точек К₂ и М₂, а затем К₁ и М₁.

Видимость прямой l, которая пересекает сферу, устанавливается по видимости точек К и М. Точка К расположена выше экватора сферы, т.е. на видимой относительно плоскости проекций П₁ половины сферы, а точка М – ниже экватора, т.е. на невидимой её половине. Поэтому относительно плоскости П₁ точка К - видимая, а точка М – невидимая. Относительно плоскости П₂ точка К – невидимая, точка М – видима, так как точка К лежит за главным меридианом, а точка М перед ним.

Решение типовых задач раздела 4. приведены на с. 38.

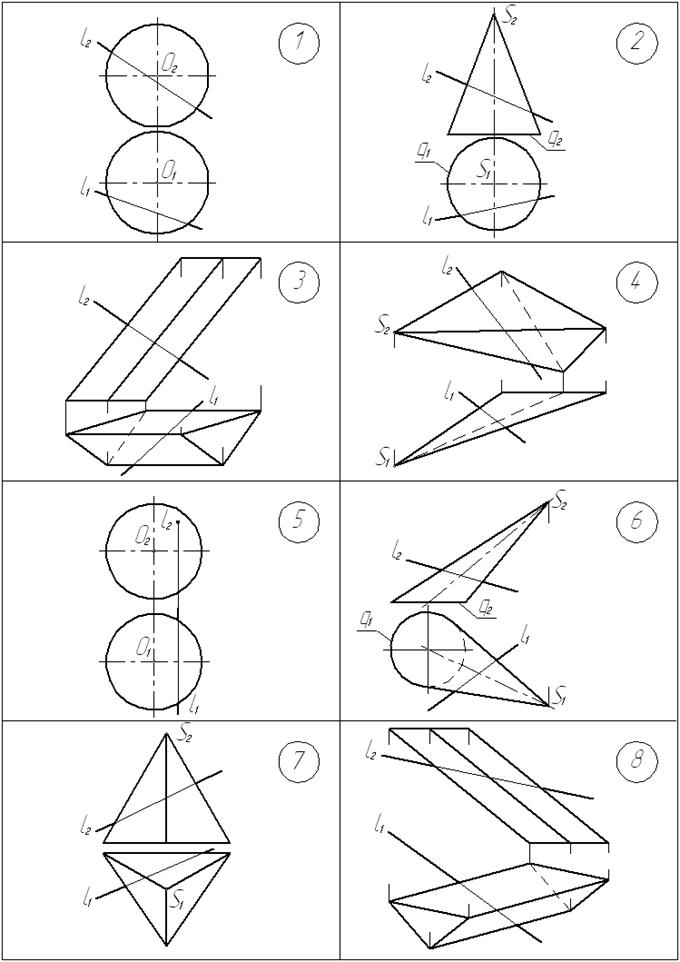
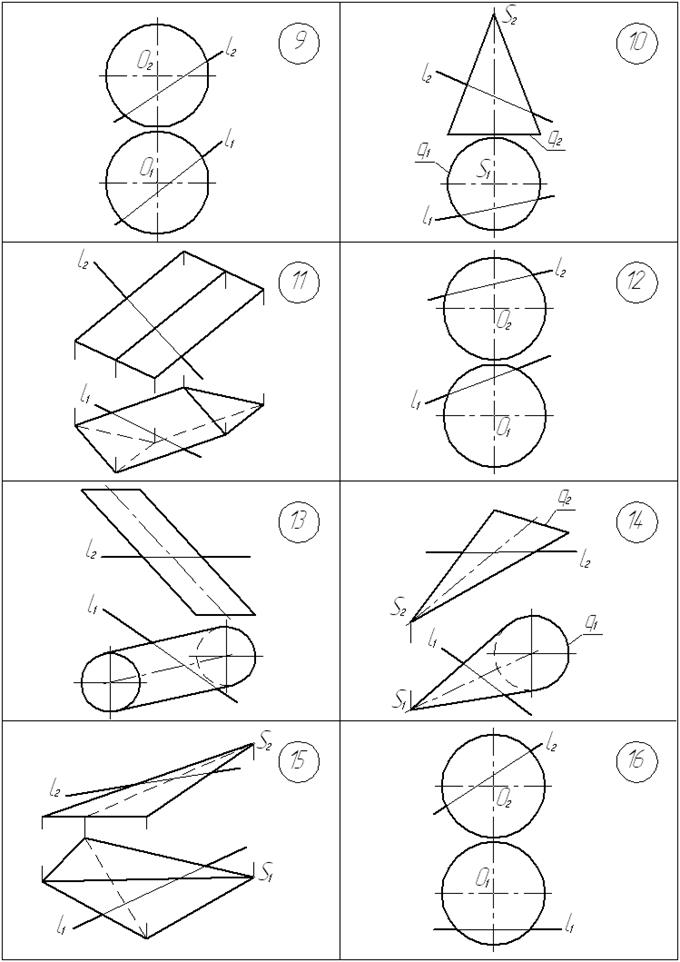
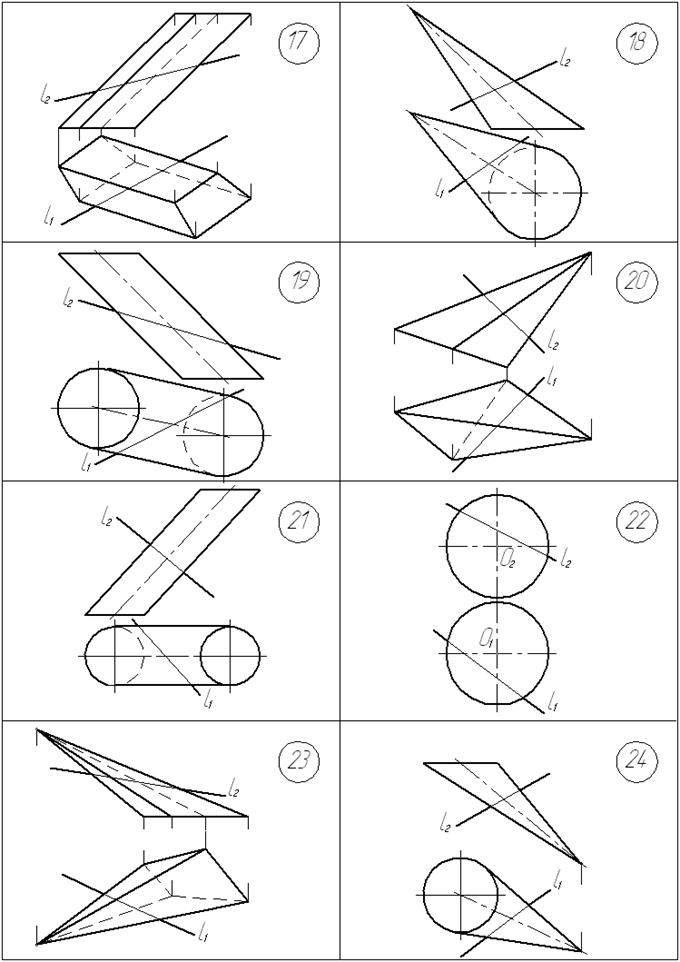
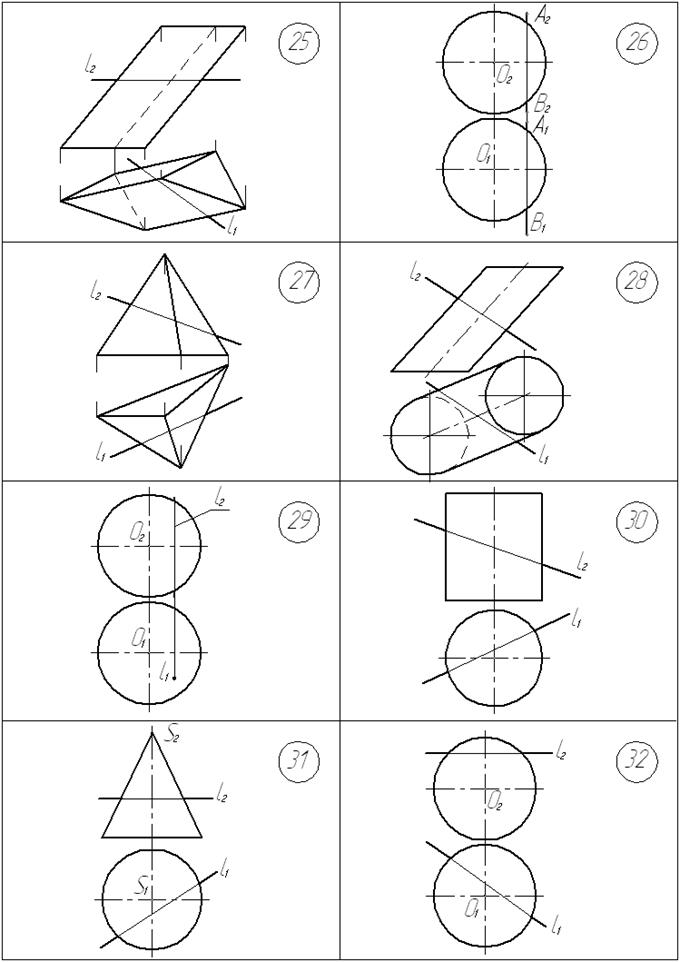
Условия задач

Графические условия задач приведены на с. 39… 42.

Построить точки К и М пересечения заданной прямой l с поверхностью.