Линейная функция, ее свойства и график
Функция, заданная формулой 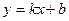 , где к и b - некоторые числа, называется линейной.
, где к и b - некоторые числа, называется линейной.
Коэффициент к=tgα характеризует угол α, который образует прямая 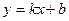 с положительным направлением оси ОХ, и называется угловым коэффициентом. Если к>0, то угол острый; если к<0, то угол тупой; если к=0, то прямая совпадает с осью Оx или ей параллельна.
с положительным направлением оси ОХ, и называется угловым коэффициентом. Если к>0, то угол острый; если к<0, то угол тупой; если к=0, то прямая совпадает с осью Оx или ей параллельна.
Свойства:
1. D(y)=R.
2. Е(y)=R.
3. Функция ни четная, ни нечетная, т.к. 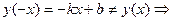 не является четной;
не является четной; 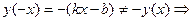 не является нечетной.
не является нечетной.
4. у = 0 при 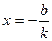 (нули функции).
(нули функции).
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при 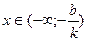 ; у > 0 при
; у > 0 при 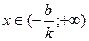 ;
;
§ если к < 0, у < 0 при 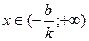 ; у > 0 при
; у > 0 при 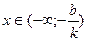 .
.
6. Функция возрастает при к>0 и убывает при к<0 на R.
7. Функция неограниченна, непрерывна.
Графиком функции является прямая. Для ее построения можно найти точки пересечения с осями координат:
§ с осью ОХ: у = 0, 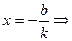 А(
А(  ; 0);
; 0);
§ с осью ОУ: х = 0, у = b 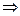 В(0; b).
В(0; b).
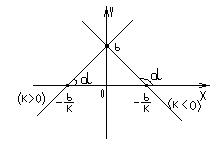
График функции 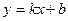 может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции
может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции 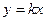 . Зависимость
. Зависимость 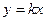 называется прямой пропорциональностью.
называется прямой пропорциональностью.
Рассмотрим частные случаи линейной функции.
Если b = 0, то 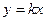 . . | Если k=0, то y=b. |
Свойства: 1. D(y)=R. 2. Е(y)=R. 3. Функция нечетная, т.к. 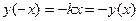 . 4. у = 0 при . 4. у = 0 при 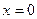 . 5. Промежутки знакопостоянства: § если к > 0, у < 0 при . 5. Промежутки знакопостоянства: § если к > 0, у < 0 при 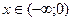 ; у > 0 при ; у > 0 при 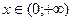 ; § если к < 0, у < 0 при ; § если к < 0, у < 0 при 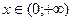 ; у > 0 при ; у > 0 при 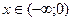 . 6. Функция возрастает при к>0 и убывает при к<0 на R. 7. Функция неограниченна, непрерывна. Графиком функции является прямая, проходящая через начало координат. . 6. Функция возрастает при к>0 и убывает при к<0 на R. 7. Функция неограниченна, непрерывна. Графиком функции является прямая, проходящая через начало координат. 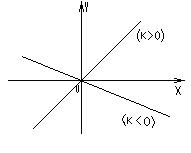 | Свойства: 1. D(y)=R. 2. Е(y)=b. 3. Функция четная, т.к. 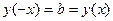 . 4. у . 4. у 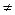 0. 5. Промежутки знакопостоянства: § если b > 0, у > 0; § если b < 0, у < 0. 6. Функция постояннана R. 7. Функция непрерывна. Графиком функции является прямая, параллельная оси Ox. 0. 5. Промежутки знакопостоянства: § если b > 0, у > 0; § если b < 0, у < 0. 6. Функция постояннана R. 7. Функция непрерывна. Графиком функции является прямая, параллельная оси Ox. 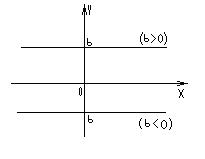 |
Функция 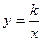 , ее свойства и график
, ее свойства и график
Если переменная у обратно пропорциональна переменной х, то эта зависимость выражается формулой 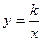 , где
, где 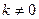 - коэффициент обратной пропорциональности.
- коэффициент обратной пропорциональности.
Свойства:
1. D(у) = 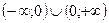 .
.
2. Е(у) = 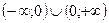 .
.
3. Нечетная, т.к. 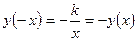 .
.
4. Промежутки знакопостоянства:
§ если k > 0, то y > 0 при 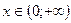 ;
;
y < 0 при 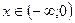 ;
;
§ если k < 0, то y > 0 при 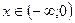 ;
;
y < 0 при 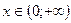 .
.
5. Монотонность:
§ при 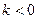 функция возрастает на
функция возрастает на 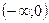 и
и 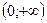 ;
;
§ при 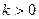 функция убывает на
функция убывает на 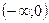 и
и 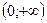 .
.
Графиком обратной пропорциональности 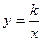 является кривая, состоящая из 2-х ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой.
является кривая, состоящая из 2-х ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой.
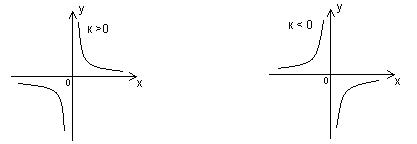
Функция 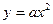 ее свойства и график
ее свойства и график
Функция вида 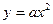 ,где а – некоторое число, а
,где а – некоторое число, а 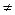 0, называется квадратичной.
0, называется квадратичной.
График функции 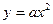 может быть получен с помощью графика функции
может быть получен с помощью графика функции 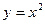 :
:
§ если а>1 , то растяжение вдоль оси Оу в а раз;
§ если 0<a<1, то сжатие вдоль оси Оу в 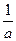 раз;
раз;
§ если а<0, то симметрично относительно оси Ох.
Рассмотрим свойства и график функции 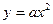 в зависимости от знака а.
в зависимости от знака а.
| а > 0 | а < 0 |
1. Д (у) = R. 2. E (y) = 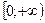 . 3.Функция четная, т.к. . 3.Функция четная, т.к. 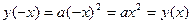 . 4. у = 0 при х = 0. 5. у>0 при . 4. у = 0 при х = 0. 5. у>0 при 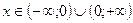 . 6. Монотонность: § функция возрастает на . 6. Монотонность: § функция возрастает на 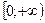 ; § функция убывает на ; § функция убывает на 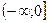 . 7. унаим = 0 при х=0. 8. Функция ограничена снизу нулем, непрерывна. . 7. унаим = 0 при х=0. 8. Функция ограничена снизу нулем, непрерывна. 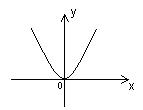 | 1. Д (у) = R. 2. E (y) = 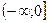 . 3.Функция четная, т.к. . 3.Функция четная, т.к. 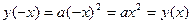 . 4. у = 0 при х = 0. 5. у<0 при . 4. у = 0 при х = 0. 5. у<0 при 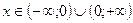 . 6. Монотонность: § функция возрастает на . 6. Монотонность: § функция возрастает на 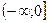 ; § функция убывает на ; § функция убывает на 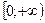 . 7. унаиб = 0 при х=0. 8. Функция ограничена сверху нулем, непрерывна. . 7. унаиб = 0 при х=0. 8. Функция ограничена сверху нулем, непрерывна. 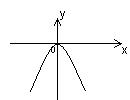 |
Графики функций 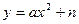 и
и 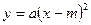 . Преобразование графика
. Преобразование графика
Графиком функции 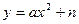 является парабола, которая может быть получена из графика функции
является парабола, которая может быть получена из графика функции 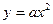 с помощью параллельного переноса вдоль оси Оy на |n|единиц вверх, если n>0; или на
с помощью параллельного переноса вдоль оси Оy на |n|единиц вверх, если n>0; или на 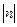 единиц вниз, если n<0.
единиц вниз, если n<0.
Рассмотрим графики функции 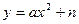 при a > 0.
при a > 0.
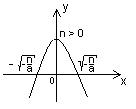
| n > 0 | n < 0 |
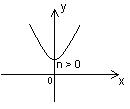 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 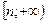 . 3. Четная. 4. Нулей нет. 5. y > 0 при . 3. Четная. 4. Нулей нет. 5. y > 0 при 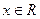 . 6. Возрастает на . 6. Возрастает на 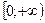 ; убывает на ; убывает на 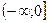 . 7. унаим = n при х = 0. 8. Ограничена снизу n, непрерывна. . 7. унаим = n при х = 0. 8. Ограничена снизу n, непрерывна. | 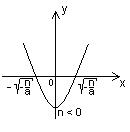 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 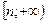 . 3. Четная. 4. у = 0 при . 3. Четная. 4. у = 0 при 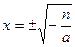 . 5. y > 0 при . 5. y > 0 при 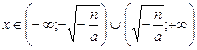 ; y < 0 при ; y < 0 при 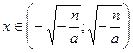 . 6. Возрастает на . 6. Возрастает на 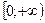 ; убывает на ; убывает на 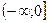 . 7. унаим = n при х = 0. 8. Ограничена снизу n, непрерывна. . 7. унаим = n при х = 0. 8. Ограничена снизу n, непрерывна. |
Рассмотрим графики функции 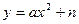 при a < 0.
при a < 0.
| n > 0 | n < 0 |
 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 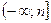 . 3. Четная. 4. у = 0 при . 3. Четная. 4. у = 0 при 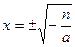 . 5. y > 0 при . 5. y > 0 при 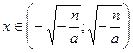 ; y < 0 при ; y < 0 при 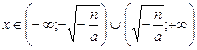 . 6. Возрастает на . 6. Возрастает на 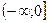 ; убывает на ; убывает на 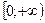 . 7. унаиб = n при х = 0. 8. Ограничена сверху n, непрерывна. . 7. унаиб = n при х = 0. 8. Ограничена сверху n, непрерывна. | 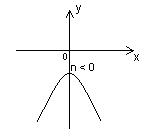 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 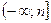 . 3. Четная. 4. Нулей нет. 5. y < 0 при . 3. Четная. 4. Нулей нет. 5. y < 0 при 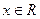 . 6. Возрастает на . 6. Возрастает на 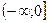 ; убывает на ; убывает на 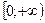 . 7. унаиб = n при х = 0. 8. Ограничена сверху n, непрерывна. . 7. унаиб = n при х = 0. 8. Ограничена сверху n, непрерывна. |
Графиком функции 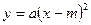 является парабола, которая может быть получена в результате параллельного переноса графика функции
является парабола, которая может быть получена в результате параллельного переноса графика функции 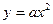 вдоль оси Оx на |m| единиц вправо, если m>0; или на |m| единиц влево, если m<0.
вдоль оси Оx на |m| единиц вправо, если m>0; или на |m| единиц влево, если m<0.
| a > 0 | a < 0 |
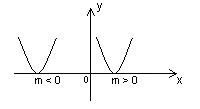 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 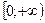 . 3. Ни четная, ни нечетная. 4. у = 0 при х=т. 5. y > 0 при . 3. Ни четная, ни нечетная. 4. у = 0 при х=т. 5. y > 0 при 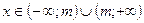 . 6. Возрастает на . 6. Возрастает на 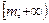 ; убывает на ; убывает на 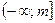 . 7. унаим = 0 при х = т. 8. Ограничена снизу нулем, непрерывна. . 7. унаим = 0 при х = т. 8. Ограничена снизу нулем, непрерывна. | 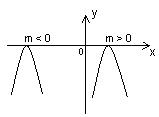 1. D(y)=R. 2. E(y)= 1. D(y)=R. 2. E(y)= 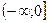 . 3. Ни четная, ни нечетная. 4. у = 0 при х=т. 5. y < 0 при . 3. Ни четная, ни нечетная. 4. у = 0 при х=т. 5. y < 0 при 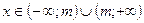 . 6. Возрастает на . 6. Возрастает на 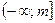 ; убывает на ; убывает на 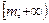 . 7. унаиб = 0 при х = т. 8. Ограничена сверху нулем, непрерывна. . 7. унаиб = 0 при х = т. 8. Ограничена сверху нулем, непрерывна. |
График функции 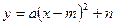 может быть получен с помощью 2-х параллельных переносов описанных выше.
может быть получен с помощью 2-х параллельных переносов описанных выше.
