Понятие функции. Область определения. Область значений. Способы задания функции. Простейшие элементарные функции
Операции над множествами
Пусть 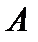 и
и 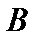 — произвольные множества.
— произвольные множества.
Объединением или суммоймножеств 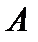 и
и 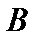 называется множество
называется множество 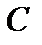 , состоящее из всех элементов, принадлежащих хотя бы одному из множеств
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств 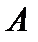 и
и 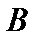 . Объединение множеств
. Объединение множеств 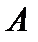 и
и 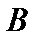 обозначается символом
обозначается символом 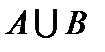 .
.
Пересечением множеств 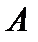 и
и 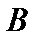 называется множество
называется множество 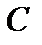 , состоящее из всех элементов, принадлежащих как множеству
, состоящее из всех элементов, принадлежащих как множеству 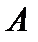 , так и множеству
, так и множеству 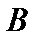 , Пересечение множеств
, Пересечение множеств 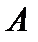 и
и 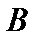 обозначается через
обозначается через 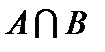 .
.
Разностьюмножеств 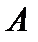 и
и 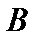 называется множество
называется множество 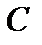 , состоящее из всех элементов, множества
, состоящее из всех элементов, множества 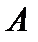 , не принадлежащих множеству
, не принадлежащих множеству 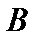 . Разность обозначается как
. Разность обозначается как 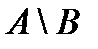 .
.
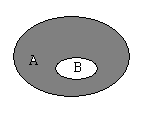
Если 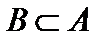 , то разность
, то разность 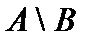 называется дополнениеммножества
называется дополнениеммножества 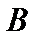 до множества
до множества 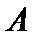 и обозначается
и обозначается 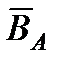 .
.
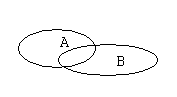
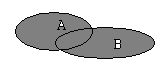
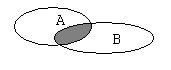
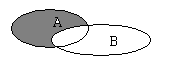
Для наглядности множества нередко изображают в виде некоторой совокупности точек на плоскости. На рис. 1а изображены множества 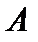 и
и 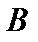 , на рис. 1б — их объединение, на рис. 1в — пересечение множеств
, на рис. 1б — их объединение, на рис. 1в — пересечение множеств 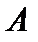 и
и 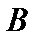 , на рис. 1г — разность множеств
, на рис. 1г — разность множеств 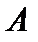 и
и 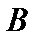 , на рис. 1д — дополнение множества
, на рис. 1д — дополнение множества 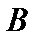 до множества
до множества 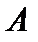 .
.
а) б) 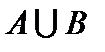 в)
в) 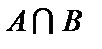
г) 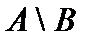 д)
д) 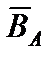
Рис. 1
Пусть задана система множеств 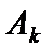 , где значения
, где значения 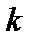 образуют некоторую совокупность индексов
образуют некоторую совокупность индексов  . Объединением
. Объединением 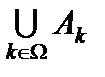 множеств
множеств 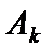 называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств
называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств 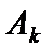 . Пересечением
. Пересечением 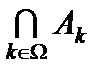 множеств
множеств 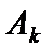 называется множество, состоящее из всех элементов, принадлежщих одновременно всем множествам
называется множество, состоящее из всех элементов, принадлежщих одновременно всем множествам 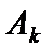 .
.
Пример. Пусть 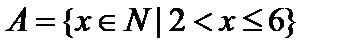 ,
, 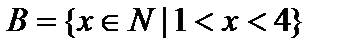 ,
, 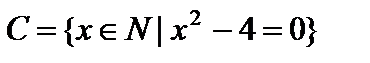 , где
, где 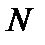 — множество натуральных чисел. Тогда
— множество натуральных чисел. Тогда
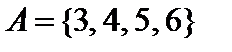 ,
, 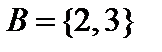 ,
, 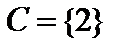 ,
,
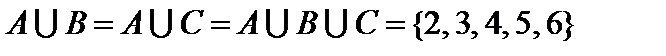 ,
, 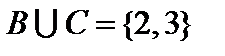 ,
,
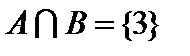 ,
, 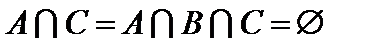 ,
, 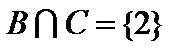 ,
,
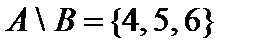 ,
, 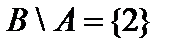 ,
, 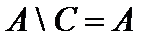 ,
, 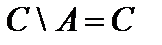 ,
, 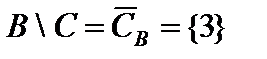 .
.
Понятие функции. Область определения. Область значений. Способы задания функции. Простейшие элементарные функции.
Понятие функции
Если каждому значению переменной 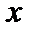 из некоторого множества
из некоторого множества 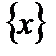 ставится в соответствие по известному закону единственное число
ставится в соответствие по известному закону единственное число 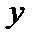 , то говорят, что на множестве
, то говорят, что на множестве 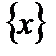 задана функция
задана функция 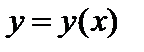 или
или 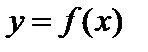 .
.
При этом 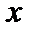 называется аргументом функции, множество
называется аргументом функции, множество 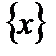 — областью задания функции
— областью задания функции 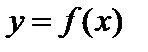 . Число
. Число 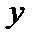 , которое соответствует данному значению аргумента
, которое соответствует данному значению аргумента 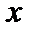 , называется частным значением функции в точке
, называется частным значением функции в точке 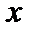 . Совокупность всех частных значений образует вполне определенное множество
. Совокупность всех частных значений образует вполне определенное множество 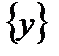 , называемое множеством значений функции.
, называемое множеством значений функции.
Функция 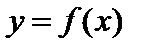 называется четной (нечетной), если для любого
называется четной (нечетной), если для любого 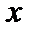 из области определения функции справедливо равенство
из области определения функции справедливо равенство 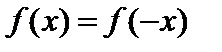 (
( 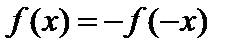 ).
).
Функция 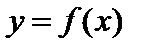 называется периодической, если существует такое число
называется периодической, если существует такое число 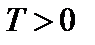 , что для любого
, что для любого 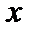 из области определения функции справедливо равенство
из области определения функции справедливо равенство 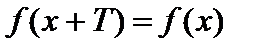 . Наименьшее из чисел
. Наименьшее из чисел 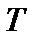 называют периодом функции.
называют периодом функции.
Функция 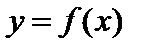 называется ограниченной на множестве
называется ограниченной на множестве 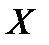 , если существует такое число
, если существует такое число 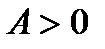 , что для любого
, что для любого 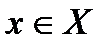 справедливо неравенство
справедливо неравенство 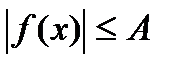 .
.
Для наглядного представления о характере функциональной зависимости часто строят графики функции.
Графиком функции 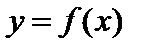 называется множество точек на плоскости с координатами
называется множество точек на плоскости с координатами 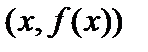 ,
, 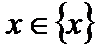 .
.
Простейшими элементарными функциями называются следующие функции: степенная 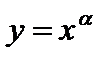 , показательная
, показательная 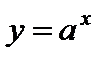 , логарифмическая
, логарифмическая 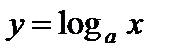 , тригонометрические функции
, тригонометрические функции 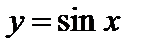 ,
, 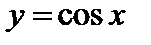 ,
, 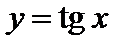 ,
, 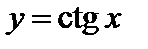 и обратные тригонометрические функции
и обратные тригонометрические функции 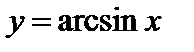 ,
, 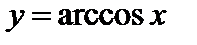 ,
, 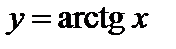 ,
, 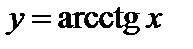 . Свойства этих функций и их графики смотрите в [1] § 5.4.
. Свойства этих функций и их графики смотрите в [1] § 5.4.
Последовательное применение двух или нескольких функций называется суперпозицией этих функций.
Функции, образованные в результате суперпозиции двух или нескольких функций будем называть сложными функциями. Например, сложная функция 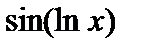 образована в результате суперпозиции функций
образована в результате суперпозиции функций 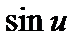 и
и 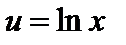 .
.
Элементарными функциями называются функции, полученные в результате суперпозиции простейших элементарных функций и арифметических действий.
