Радиусы поперечных сечений в процессе кручения не искривляются и сохраняют свою длину

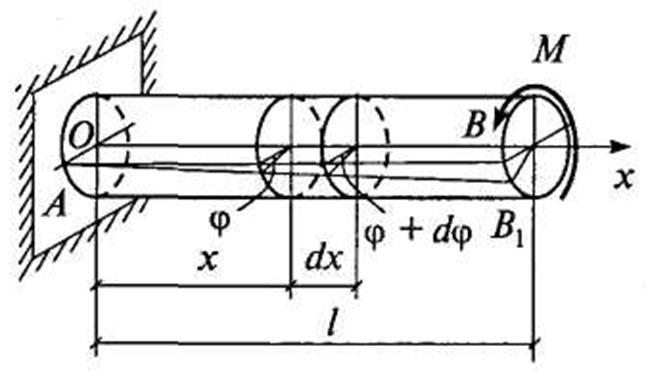
Рис. 5.11

В результате взаимного поворота поперечных сечений проис­ходит перекос прямых углов элемента, т.е. возникают угловые деформации γ. При этом, величина γ из­меняется в зависимости от переменного радиуса rпо линейно­му закону и имеет наибольшее значение γ_нб в точках боковой поверхности.

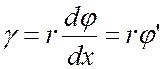. (5.10)

Деформации сдвига возникают от касательных напряжений τ, действующих согласно закону парности в поперечных и про­дольных сечениях стержня.

Рассмотрим напряженное состояние стержня. Согласно зако­ну Гука при сдвиге с учетом формулы (5.10) получим

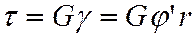. (5.11)

Касательные напряжения, действующие в поперечных сечени­ях стержня, приводятся к крутящему моменту М_к.

,

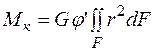Величина

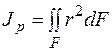
представляет собой полярный момент инерции сечения. Для сплошного круглого сечения он равен

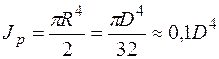. (5.12)

С учетом этого выразим относительный угол закручивания через крутящий момент

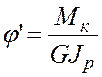. (5.13)

Величина GJ_p , входящая в эту формулу, называется жесткос­тью круглого стержня при кручении.

Подставляя найденную величину φ'в равенство (5.11), полу­чим формулу для определения касательных напряжений в попе­речных сечениях круглого стержня при кручении

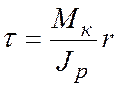. (5.14)

Из этой формулы видно, что касательные напряжения в по­перечном сечении изменяются в радиальном направлении по линейному закону (рис. 5.12). Наибольшее значение они прини­мают на контуре сечения приr = R

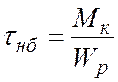. (5.15)

где W_p — полярный момент сопротивления, равный

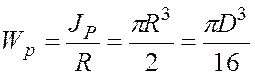. (5.16)

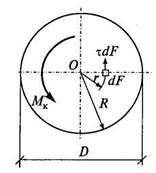
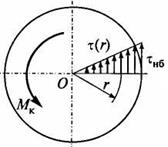
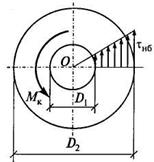
Рис. 5.12 Рис. 5.13 Рис. 5.14

Формулы (5.13) — (5.15) справедливы также для трубчатого стержня (рис. 5.14). При этом полярный момент инерции и по­лярный момент сопротивления равны

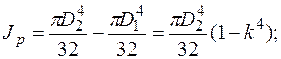
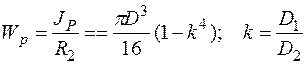. (5.17)

Определение углов закручивания стержней круглого сечения.Интегрируя равенство (5.13) по длине стержня в пределах от 0 до х, получим выражение для угла закручивания

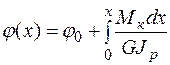. (5.18)

где φ₀ — угол закручивания начального сечения. Если начальное сечение закреплено, то φ₀ = 0. В частном случае, когда М_к= const, GJ_p = constи левый конец закреплен (рис. 5.17), получим

.

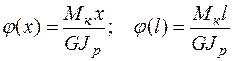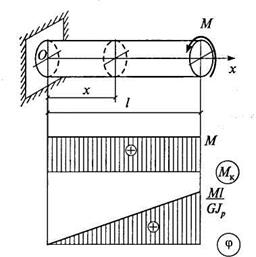
Рис. 5.15

Эпюры М_к и φ для этого случая приведены на рис. 5.15.

При нагружении стержня равномерно распределенным скру­чивающим моментом т (рис. 6.10) крутящий момент в произ­вольном сечении х равен М_к =ml– тх, где М₀= ml — реактив­ный момент в заделке.

Для определения углов закручивания подставим это выраже­ние в формулу (5.18), принимая φ₀ = 0. После интегрирования получим

.

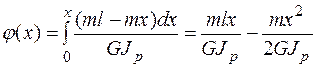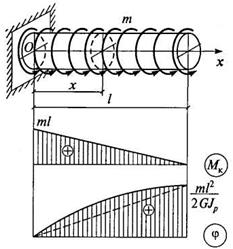
Рис. 5.16

Эпюры М_к и φ приведены на рис. 5.16. Угол закручивания изменяется по закону квадратной параболы.

Расчет стержней круглого сечения на прочность и жесткость.Кручение как основной вид деформации характерно для эле­ментов машиностроительных конструкций.

Усло­вие прочности при кручении стержней круглого сечения имеет вид

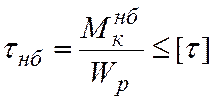, (5.19)

где 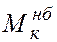— наибольший крутящий момент в стержне от действия нормативных нагрузок; W_p— полярный момент сопротивления; [τ] — допускаемое касательное напряжение.

Из условия прочности (5.19) получим формулу для подбора сечения

.

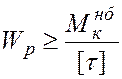Отсюда находим требуемые размеры сечения стержня. Для стержня сплошного круглого сечения с учетом (5.16) имеем

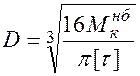. (5.20)

Для трубчатого стержня с учетом (5.17)

.(5.21)

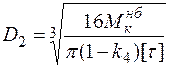
Стержни, работающие на кручение, должны обладать доста­точной жесткостью. Условие жесткости при кручении имеет вид

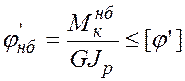, (5.22)

где [φ'] — допускаемый относительный угол закручивания, обычно принимаемый в пределах 0,15 ÷ 2 град/м.

Из условия жесткости (5.22) имеем

.

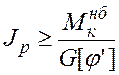Отсюда находим требуемые размеры поперечного сечения стержня. Для стержня сплошного круглого сечения с учетом (5.12) имеем

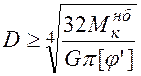. (5.23)

Для трубчатого стержня с учетом (5.17) получим

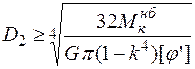. (5.24)

При расчете стержня на прочность и жесткость из двух тре­буемых значений диаметра надо принять большее.

Допускаемое напряжение при кручении :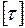

для хрупких материалов

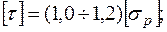
для пластических материалов

.

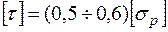3.ПОСТРОЕНИЕ ЭПЮР КРУТЯЩИХ МОМЕНТОВ

Пример 1. Построить эпюру крутящих моментов для вала.

1. Изображаем расчетную схему (рис. 5.17,а).Реакцию в заделке определять не обязательно, так как в соответствии с методом сечений можно отбрасывать каждый раз правую часть вала с заделкой. Вал имеет четыре силовых участка:

Iучасток :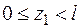

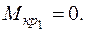
IIучасток :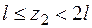

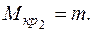
IIIучасток :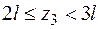

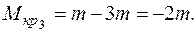
IVучасток :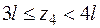

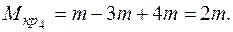
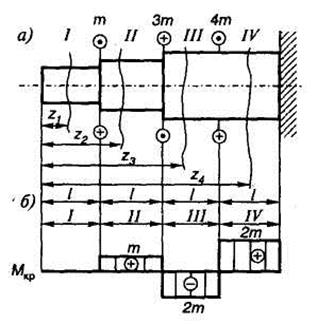
Рис. 5.17

2. Строим эпюру крутящих моментов 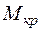(рис. 5.17, б).

Выполняем проверку правильности эпюры. Место расположения скачков, их направление и величина соответствуют внешним прило­женным крутящим моментам.