Занятие 2. Двумерные массивы
У двумерного массива имеется два индекса: i – номер строки, j – номер столбца.
Индексация двумерного массива представлена на рис. 4.
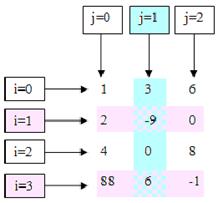
Рис. 4 Индексация двумерного массива
Для использования двумерного массива в программе необходимо:
1. Объявить массив в функции main():
тип_данных имя_массива [количество строк][количество столбцов];
double a[5][9]; // двумерный массив из 5 строк, 9 столбцов
2. Проинициализировать массив;
3. Провести вычисления, исследования.
Способы инициализации двумерного массива a[n][m] представлены в таблице 4. Обратим внимание на то, что числа n и m известны заранее и в программе фигурировать не будут.
Таблица 4
Способы инициализации двумерного массива a[n][m]
| Часть блок-схемы | Часть программы |
1. из файла: 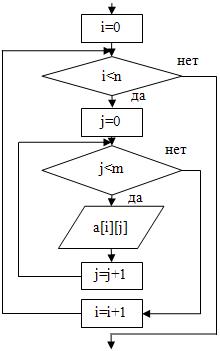 | double a[n][m]; int i,j; fstream file; file.open(“1.txt”, ios::in); for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ file>>a[i][j]; } } file.close(); |
2. по заданной формуле a[i][j]=f(i,j): 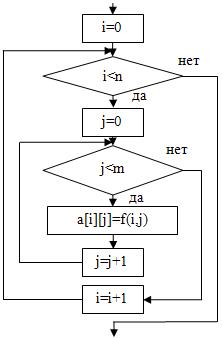 | double a[n][m]; int i,j; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ a[i][j]=f(i,j); } } |
Примечание. Двумерный массив также можно проинициализировать и заранее определенными числами, и с клавиатуры. Но данные способы неудобны для двумерных массивов, т.к. они содержат слишком много элементов.
Вывод двумерного массива на экран представлен в таблице 5.
Таблица 5
Вывод двумерного массива на экран
| Часть блок-схемы | Часть программы |
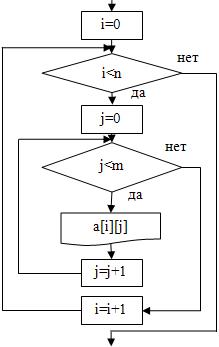 | for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ cout<<setw(6)<<a[i][j]; } cout<<endl; } |
Принципы нахождения таких величин, как сумма, произведение, минимальное, максимальное значение, представлены в таблице 6.
Таблица 6
Принципы исследования двумерного массива
| Часть блок-схемы | Часть программы |
1. нахождение суммы: 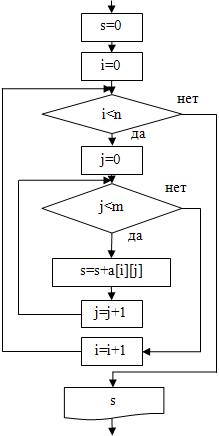 | s=0; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ s=s+a[i][j]; } } cout<<”s=”<<s<<endl; |
2. нахождение произведения: 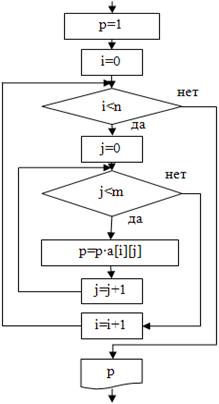 | p=1; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ p=p*a[i][j]; } } cout<<”p=”<<p<<endl; |
3. нахождение среднего арифметического и количества элементов: 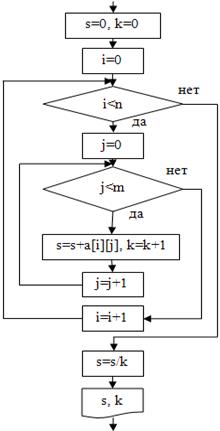 | s=0, k=0; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ s=s+a[i][j]; k=k+1; } } s=s/k; cout<<”s=”<<s<<endl; cout<<”k=”<<k<<endl; |
4. нахождение максимального элемента: 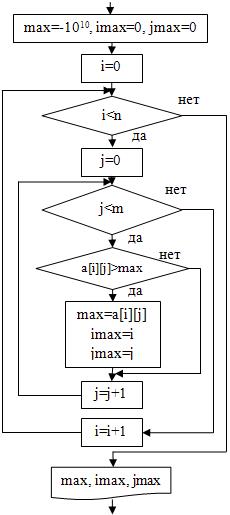 | max=-10E10; imax=0; jmax=0; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ if(a[i]>max){ max=a[i][j]; imax=i; jmax=j; } } } cout<<”max=”<<max<<endl; cout<<”imax=”<<imax<<endl; cout<<”jmax=”<<jmax<<endl; |
5. нахождение минимального элемента: 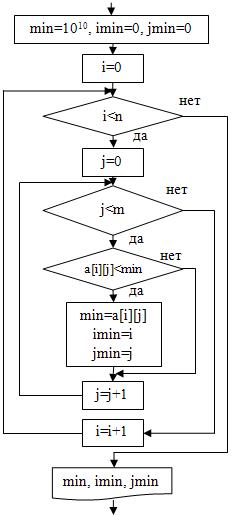 | min=10E10; imin=0; jmin=0; for(i=0; i<n; i=i+1){ for(j=0; j<m; j=j+1){ if(a[i][j]<min){ min=a[i][j]; imin=i; jmin=j; } } } cout<<”min=”<<min<<endl; cout<<”imin=”<<imin<<endl; cout<<”jmin=”<<jmin<<endl; |
6. поменять элементы i1, j1 и i2, j2 местами: 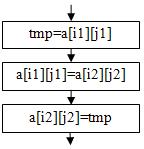 | tmp=a[i1][j1]; a[i1][j1]=a[i2][j2]; a[i2][j2]=tmp; |
7. поменять местами строки i1 и i2: 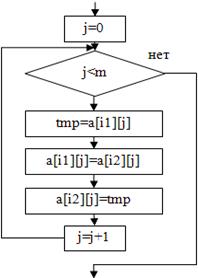 | for(j=0; j<m; j=j+1){ tmp=a[i1][j]; a[i1][j]=a[i2][j]; a[i2][j]=tmp; } |
8. поменять местами столбцы j1 и j2: 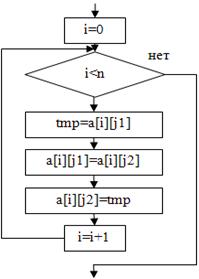 | for(i=0; i<n; i=i+1){ tmp=a[i][j1]; a[i][j1]=a[i][j2]; a[i][j2]=tmp; } |
9. вычисление формулы 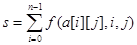 :  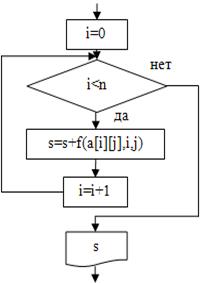| s=0; for(i=0; i<n; i=i+1){ s=s+f(a[i][j],i,j); } cout<<”s=”<<s<<endl; |
Условия для исследования квадратной матрицы (количество строк и столбцов совпадает):
для элементов на главной диагонали: i=j;
для элементов над главной диагональю: i<j;
для элементов под главной диагональю: i>j;
для элементов на побочной диагонали: i+j=n-1;
для элементов над побочной диагональю: i+j<n-1;
для элементов под побочной диагональю: i+j>n-1.
Примечание. Если требуется определить, например, сумму элементов, находящихся над главной диагональю, то задаем двумерный цикл по i, j и в теле цикла ставим дополнительное условие «i<j»
Пример 3. Массив а(6, 8) задан формулой аi,j=3i-5j. Найти сумму элементов во второй строке, поменять местами первую и третью строки, найти произведение по формуле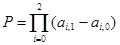 
.
Решение. Данную задачу можно разбить на несколько этапов:
1. задать массив по формуле и вывести его на экран;
2. найти сумму элементов во второй строке и вывести ее на экран;
3. поменять местами первую и третью строки;
4. вывести на экран измененный массив;
5. найти произведение по формуле и вывести его на экран.
Каждый указанный этап решается с помощью циклов. Все циклы целесообразно использовать с предусловием (в программе – оператор for). На первом этапе следует организовать двумерный цикл по i, по j, т.к. необходимо задать значениями и вывести на экран весь массив. На втором этапе перед циклом необходимо задать S=0, а в теле цикла по j насчитывать значение S. Индекс i задаем как 1, что соответствует второй строке. Следует отметить, что нельзя считать сумму по какой-то определенной строке (столбце, диагонали) внутри двумерного цикла, т.к. в этом случае S будет больше в разы (зависит от количества строк/столбцов).На третьем этапе индексы строк берем i=0 – для первой строки, i=2 – для третьей строки. Замена строк организуется в одномерном цикле по j. На четвертом этапе матрица а должна быть отображена на экране. Нам требуется показать, что замена строк выполнена верно.На пятом этапе перед циклом следует задать P=1, а в теле цикла насчитывать произведение. Цикл организуем одномерный по i от 0 до 2 включительно, т.к. согласно формуле изменяется только i.
Блок-схема для примера 3 приведена на рис. 5.
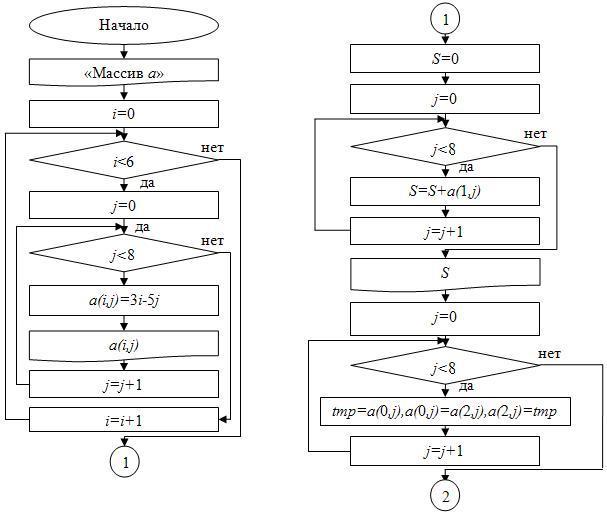
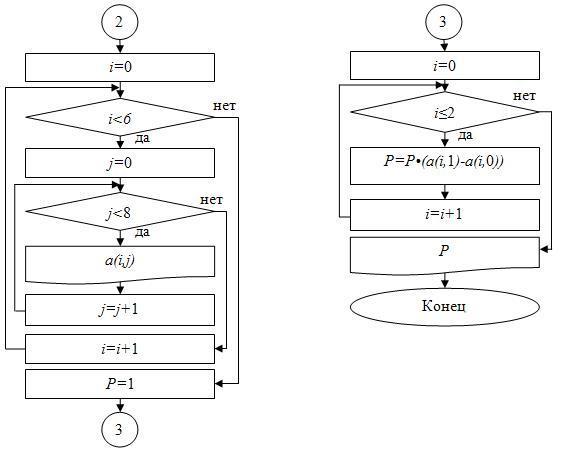
Рис. 5 Блок-схема для примера 3
Код программы (Visual Studio) с оператором for:
// proga29.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double a[6][8];
double S, tmp, P;
int i, j;
cout<<"Massiv a:"<<endl;
for(i=0; i<6; i=i+1){
for(j=0; j<8; j=j+1){
a[i][j]=3.0*i-5.0*j;
cout<<setw(5)<<a[i][j];
}
cout<<endl;
}
S=0;
for(j=0; j<8; j=j+1){
S=S+a[1][j];
}
cout<<"S="<<S<<endl;
for(j=0; j<8; j=j+1){
tmp=a[0][j];
a[0][j]=a[2][j];
a[2][j]=tmp;
}
for(i=0; i<6; i=i+1){
for(j=0; j<8; j=j+1){
cout<<setw(5)<<a[i][j];
}
cout<<endl;
}
P=1;
for(i=0; i<2; i=i+1){
P=P*(a[i][1]-a[i][0]);
}
cout<<"P="<<P<<endl;
return 0;
}
Результат выполнения программы:
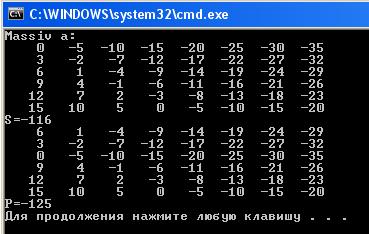
Краткие итоги:
Самыми распространенными видами массивов являются одномерные и двумерные массивы. Статические массивы легко задавать и использовать в программе. Циклы делают работу с массивами удобной и доступной.
Вопросы:
1. Что такое массив?
2. Перечислите виды массивов.
3. Что такое индекс?
4. Как добиться отображения массива на экране в виде ровной таблицы?
Упражнения:
1. Одномерный массив Х(8) задать в программе. Найти максимальный из отрицательных элементов и поменять его местами с последним.
2. Одномерный массив Х(10) задать с клавиатуры. Найти сумму отрицательных, количество положительных и произведение ненулевых элементов.
3. Одномерный массив Х(15) задать числами. Найти среднее арифметическое элементов, удовлетворяющих условию cos(xi)<0.
4. Одномерный массив Х(12) задать по формуле X[i]=ln(i+0,1). Найти количество элементов, удовлетворяющих условию -0,5<sin(xi)≤0, минимальный элемент.
5. Матрицу А(5,5) задать по формуле A[i,j]=4sin(7,1i+j). Найти новый одномерный массив С из произведений элементов каждой строки матрицы А. Найти максимальный элемент среди положительных элементов матрицы А. Заменить третий элемент в первой строке матрицы А на найденный максимальный элемент.
6. Матрицу А(7,7) задать по формуле А[i,j]=sin(0,1j+i). Найти сумму положительных элементов над главной диагональю матрицы. Найти максимальный элемент среди отрицательных элементов 4-ой строки. Заменить найденный максимальный элемент значением суммы.
7. Матрицу А(5,3) задать по формуле А[i,j]=sin(i+0,4)+cos(j+0,2). Поменять местами первую и последнюю строки матрицы. Подсчитать Si для элементов каждой строки матрицы по формуле: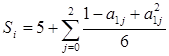 
, где i – номер строки.