Решение систем линейных уравнений методом Гаусса

Лекция 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Определение. Системой линейных алгебраических уравнений, содержащей m урав­нений с n неизвестными, называется

,

,

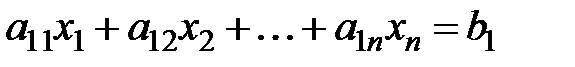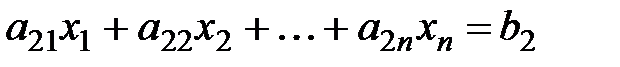(1)

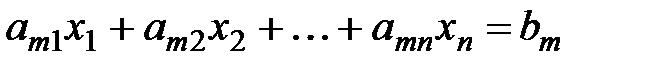
где х_j –неизвестные, числа а_ij, 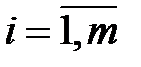, 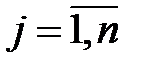называются коэффициентами при неизвестных, числа b_i— свободными членами.

Такую систему удобно записывать в матричной форме

А · Х = В.

Здесь А — матрица из коэффициентов при неизвестных, называемая основной матрицей:

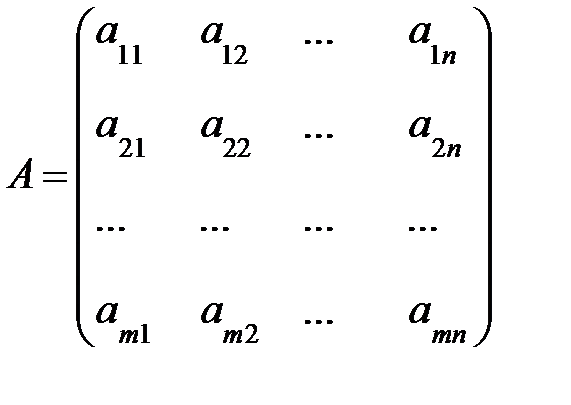
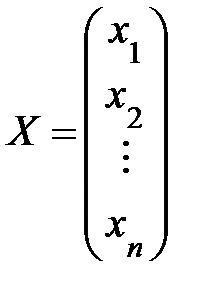— вектор-столбец из неизвестных x_j ,

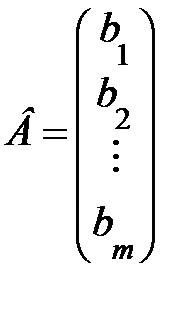— вектор-столбец из свободных членов b_i .

Расширенной матрицей системы называется матрица 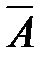системы, до­полненная столбцом свободных членов

.

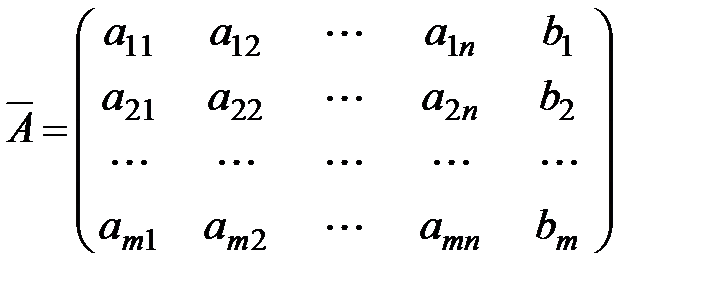Решением системы называется n значений неизвестных х₁ = c₁, x₂ = c₂, . . . , x_n = c_n , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .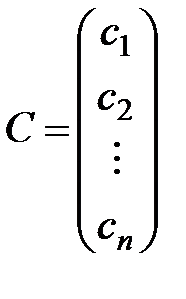

О. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы называются эквивалентными (равносильными), если каждое решение одной из них является решением другой, и наоборот.

Т. При элементарных преобразованиях строк расширенной матрицы системы получаются эквивалентные системы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

,

.

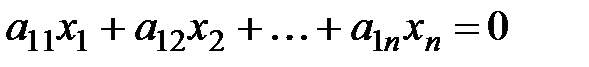Однородная система всегда совместна, так как х₁ = х₂ = . . . = х_n = 0 является решением системы. Это решение называется нулевым или три­виальным.

Решение систем линейных уравнений

Пусть дана произвольная система m линейных уравнений с n неизвестными (1)

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и толь­ко тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Если ранг совместной системы равен числу неизвестных, то система определенная.

Если ранг совместной системы меньше числа неизвестных, то система неопределенная.

Матричный способ

Пусть дана система n линейных уравнений с n неизвестными (m = n)

,

,

………………………..

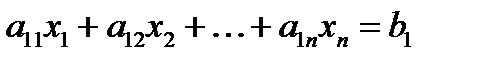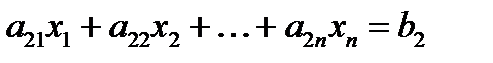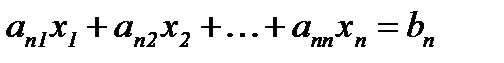
или в матричной форме А • X = В.

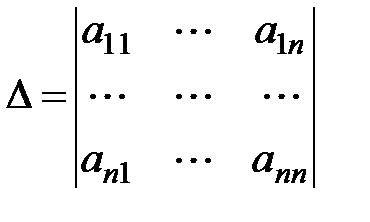
называется определителем системы. Если Δ ≠ 0, то система имеет единственное решение.

Матричный способ. Пусть Δ ≠ 0 .

Умножив обе части уравнения А • X = В слева на матрицу A^-1, полу­чим A^-1 • А • Х = A^-1 • B . Поскольку A^-1 • А = Е и Е • X = X, то

X = A^-1 • B. (2)

Отыскание решения системы по формуле (2) называют матричным способом решения системы. Пример.

Формулы Крамера

Пусть Δ ≠ 0 .

, ,..

, , , . . . , .

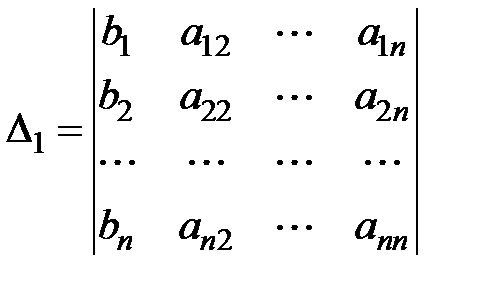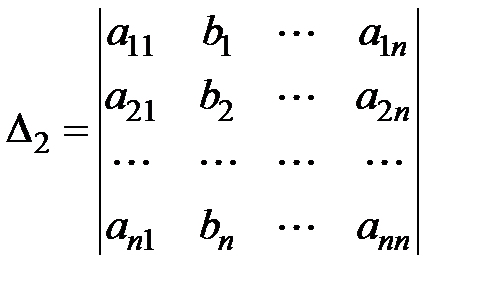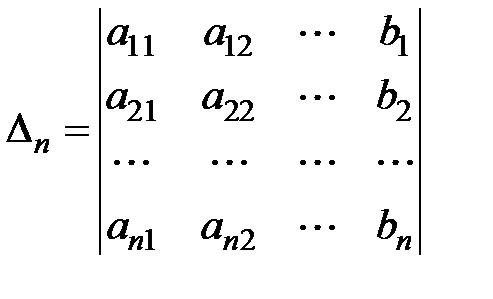
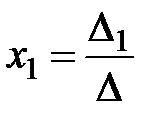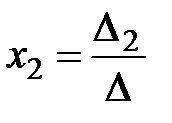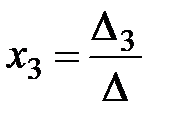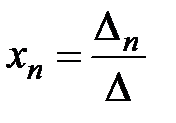Формулы 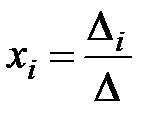, 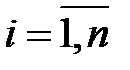(3)

называются формулами Крамера.

Пример. Решить систему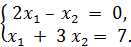

Решение: 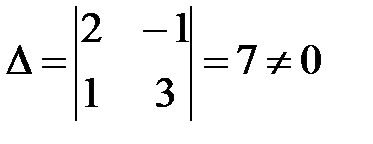, , 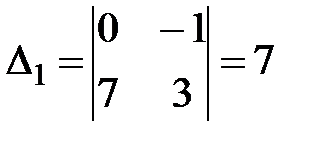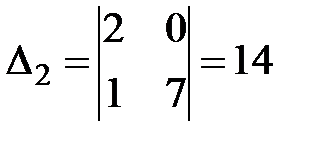. Значит,

, .

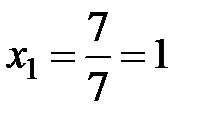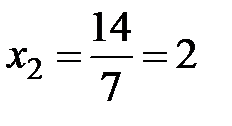Решение систем линейных уравнений методом Гаусса

Пример. Решить систему методом Гаусса:

,

,

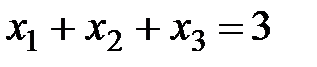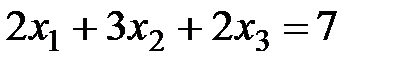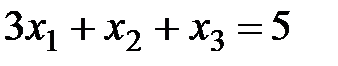
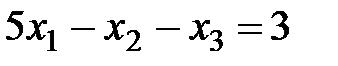
Решение: Произведем элементарные преобразования над строками расширенной матрицы системы:

~ ~ ~

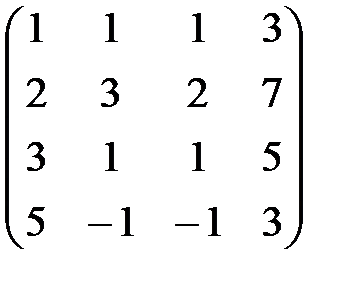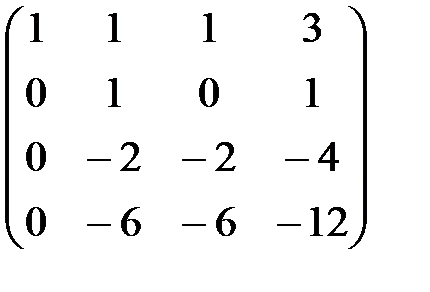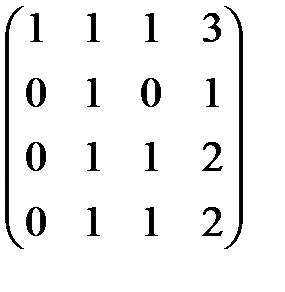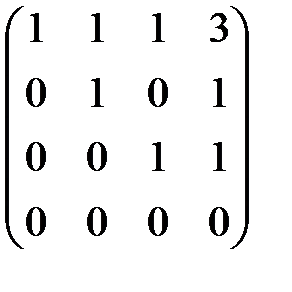
Полученная матрица соответствует системе

x₁ + x₂ + x₃ = 3 ,

x₂ = 1 ,

x₃ = 1 .

Осуществляя обратный ход, находим х_з = 1, х₂ = 1, х₁ = 1.