Формирование логико-математических понятий у младших школьников

Изучая математику в школе, колледже, вузе, необходимо усвоить определенную систем} понятий, предложений и доказательств, но чтобы овладеть этой системой и затем успешно применять приобретенные знания и умения, обучая младших школьников и решая задачу их развития средствами математики, нужно сначала понять, каковы особенности математических понятий, как устроены их определения, предложения, выражающие свойства понятий, и доказательства. Такие знания нужны учителю начальных классов еще и потому, что он первым вводит детей в мир математических знаний, и от того, как грамотно и успешно он это делает, зависит и отношение ребенка к изучению математики в целом.

Изучение этого материала связано с овладением теоретико-множественным языком, который будет использоваться не только при рассмотрении логической структуры математических понятий, предложений и доказательств, но и при построении всего курса математики начальной школы.

Стойлова Л.П. к элементам логики относит следующие разделы математического знания:

1. Множества и операции над ними. 2. Математические понятия. 3. Математические предложения. 4. Математическое доказательство. 5. Текстовая задача и процесс се решения 6. Комбинаторные задачи и их решения. 7. Алгоритмы и их свойства.

Рассмотрим линию логико-математических понятий и отношений.

Содержание этой линии представляют следующие вопросы: высказывание; примеры различных верных и неверных высказываний; числовые равенства и неравенства как высказывания; свойства числовых равенств; предложение с переменной; уравнение и неравенство.

Может возникнуть вопрос, почему уравнение и неравенство, которые обычно относят к алгебраическим понятиям, связывают с логико-математической линией. Дело в том. что на уравнение и неравенство в данной системе смотрят гораздо шире, чем это принято в начальной школе, где традиционно х в уравнении или неравенстве - это лишь неизвестное число, которое нужно найти с помощью вычислений. Поэтому сами эти понятия у младших школьников недостаточно отчетливо сформированы. Так. уравнением многие дети считают такие записи, как 5 + 7 ==12..г

В соответствии с высказанным подходом уравнение и неравенство предстают перед учащимися как математические примеры предложений с переменной. Подставляя вместо переменной различные ее значения (числа), дети получают высказывания, определяют, при каких значениях получившееся высказывание верное, а при каких - неверное. При этом вводятся понятия «корень уравнения» и «решение неравенства».

- Хотя уравнения и неравенства - это «точки» пересечения логико-математической и алгебраической линий, вопрос о способах решения уравнений и неравенств отнесем к чисто алгеб­раической линии и рассмотрим его позднее.

В математической логике высказыванием называют утверждение, о котором можно точно сказать, какое оно: истинное или ложное (термины «истинное», «ложное» будут вво­диться в четвертом классе; третьеклассники пользуются терминами «верное» и «неверное» высказывание и вместо термина «утверждение» употребляют слово «предложение»). Итак, высказывание - это предложение, о котором можно сказать, верное оно или неверное. Так, высказывание «Москва - столица России» - верное, а высказывание «В июне 31 день» - неверное.

В учебнике приводятся примеры предложений, не являющихся высказываниями. О них нельзя сказать, верные они или неверные. Высказываниями не являются любые вопросительные и восклицательные предложения (например: «Который час?». «С Новым годом!»), поговорки (обычно образные выражения, не составляющие законченного высказывания) или такие предложения, истинность которых в данный момент нельзя проверить (например. «Сегодня будет дождь»). Авторы предупреждают: не стремитесь научить каждого ученика отличать высказывание от предложения, не являющегося высказыванием. Важно лишь, чтобы дети поняли, что не каждое предложение является высказыванием.

Как сказано выше, примерами высказываний являются числовые равенства и неравенства. Так. 15 + 25 = 40 - верное числовое равенство, а 28 : 4 = 8 - неверное числовое равенство; числовое неравенство 135 > 70 верное, а числовое неравенство 20 • 8 < 100 неверное.

Характерно, что в начальной школе традиционно рассматриваются только верные равенства и неравенства. С неверными равенствами и неравенствами дети практически не встречаются. Поэтому они, естественно, считают, что в неверном равенстве или неравенстве (например, 3+4=8, 5 > 9) неправильно поставлен знак равенства или неравенства. Это вызовет затруднения в дальнейшем - при обучении решению уравнений и неравенств.

В третьем классе учащиеся знакомятся с простейшими свойствами числовых равенств и неравенств. Равенство (неравенство) не нарушится, если к обеим его частям прибавить или из обеих его частей вычесть одно и то же число. Обе части равенства или неравенства можно умножить или разделить на одно и то же натуральное число. На основе этих свойств можно легко решать некоторые виды уравнений. Например, уравнение 186 + х =35 + 186 легко решить, вычитая из обеих его частей число 186. Получится х =35. Корень виден сразу: 35.

Теперь обратимся к предложениям, содержащим переменную.

О предложении, содержащем переменную, нельзя сказать, верно оно или неверно, пока не подставлено вместо переменной ее значение. Поэтому предложение с переменной высказыванием не является. Такое предложение в математической логике часто называют высказывательной формой (в третьем классе этот термин не используется).

Рассмотрим примеры. «Город X находится в России». Если значением X является Тула, то данное предложение становится верным высказыванием: «Город Тула находится в России». При другом значении X предложение «Город X находится в России» обращается в неверное высказывание. Так, если Л-Лондон, то высказывание «Город Лондон находится в России» неверное.

Формальное определение понятия «уравнение» учащимся не дается, но они должны хорошо понимать, что уравнение - это, во-первых, равенство (т.е. в записи уравнения обязательно должен быть знак равенства =), во-вторых, в нем должна быть переменная; следовательно, уравнение - это равенство с переменной.

Введя термин «уравнение» и ознакомив детей с его смыслом, полезно предложить им прочитать записи: 3 + 4. 7 - х, 9+х=15. 24:3° 8. х+4, х=3. К) - 7 ° 3. найти среди них уравнение и доказать, что это уравнение.

Рассматривая записи, дети найдут среди них ту. которая является уравнением: 9+ х = 15. Далее надо проверить два условия: 1) является ли оно равенством. 2) есть ли в нем переменная.

Предположим, ученик говорит, что это уравнение, так как в записи сеть х. Тогда возразите ему: «Но в записи 7-х тоже есть х, а ведь это не уравнение». Ученик может сказать, что в записи есть знак =. Снова возразите: «Но ведь в записи 24 : 3 = 8 тоже есть знак =. а это не уравнение». Надо добиться того, чтобы ученик сказал, что запись 9 + х = 15- уравнение, так как в нем есть знак = и переменная х.

Для тренировки полезно предложить учащимся доказать, что каждая из остальных записей уравнением не является. Можете поставить вопросы и иначе: «А мне кажется, что 10-7=3— уравнение. Права ли я? Почему нет'.' Ну. тогда х + 4 - уравнение. Верно ли это?

Можете считать, что у Ваших учеников хорошо сформировано понятие уравнения, если они понимают, что в уравнение вместо буквы нужно подставить число. В зависимости от числа, которое подставляется вместо буквы, получается верное или неверное равенство. Так. если в уравнение 3 + х = 9 вместо х подставить, например. 5. то получится неверное равенство 3+5=9. Можно подставить и другие числа. Но только при х. равном 6. получается верное равенство 3+6=9. Число 6 называют корнем этого уравнения. Термин «корень» вводится в третьем классе и входит в активный словарь учащихся.

Упражнения логического характера, содержащиеся в учебнике математики 1 класса Рудницкой В.Н.

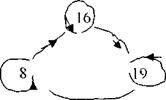
Известно, что 16 меньше 17, 17 меньше 18, 16 меньше 18. Изобрази все три высказывания на одном графе. Сколько точек (вершин графа) нужно отметить? Сколько будет стрелок (ребер графа)9

Составь и прочитай все верные высказывания.

Из корзины с зелеными и желтыми яблоками, не глядя, достают одно за другим 7 яблок. Сколько желтых и сколько зеленых яблок может среди них оказаться9

Из книги выпало несколько листов. На первой выпавшей странице стоит номер 9, а на последней - номер 12. Сколько листов выпало из книги9

Из ящика с зелеными и желтыми грушами, не глядя, взяли 2 груши. Верно ли, что эти груши будут обязательно одного цвета

4. Методические основы организации контроля и оценки знаний при обучении младших школьников математике в Образовательной сис­теме «Школа XXI века»

В Образовательной системе «Школа XXI » при осуществлении контроля результатов обучения педагоги, в первую очередь, стремятся проконтролиро­вать, как учащиеся овладевают качествами функционально грамотной лично­сти, т.е. не отдельными знаниями, а умениями ими пользоваться в ходе ре­шения различных задач (проблем). Для реализации данной цели контроля ав­торы и методисты Образовательной системе «Школа XXI » разработали «Дневник школьника - XXI » для 3-4 классов. В нем уже в самом начале обо­значены цели изучения предметов, в том числе и математике, в виде необхо­димых общеучебных и предметных умений, сформулированных в доступном для 10-11 летних детей виде. Ознакомление ученика и родителей с этими це­лями сделает процесс обучения более мотивированным.

На уроке определение качественного уровня задания и правильности его выполнения должно осуществляться по соглашению учителя и учеников. Опираясь на перечень требований государственного минимума и требования программы, учитель и ученики в диалоге договариваются, какие вопросы и задания к какому уровню они относят. В дальнейшем при использовании уже оговоренных однотипных вопросов обсуждение проводить не нужно, если не возникает сомнения с какой-либо стороны. При появлении нового типа зада­ний нужно достичь нового соглашения.

Точно также для определения успешности выполнения задания надо дать возможность сначала самому ученику свериться с неким эталоном, кри­териями правильности и т.д. После этого ученик сам оценивает свою успеш­ность, а учитель высказывает свое мнение - происходит согласование.

Как и в традиционной системе обучения, в Образовательной программе «Школа 2100» пользуются основными видами контроля, но вносят в них свои коррективы.

Текущий контроль - решение задач в процессе открытия нового знания на каждом уроке. В тот момент, когда ученик только учится, оценка обяза­тельна. При этом оценка - гибкий инструмент, который готовит школьника. Оценивается не столько обученность, сколько учебная деятельность ученика - его старательность. В противном же случае, если прямо на уроке стремить­ся всем и определять оценки, и, особенно, выставляя отметки, хорошими учениками будут только «шустрики», а «мямлики» окажутся плохими.

Тематический контроль - решение задач в письменных самостоятель­ных работах по итогам изучения темы. Здесь имеет смысл проверять уже обученность, а не старательность. Самостоятельные и контрольные работы по математике представлены в виде специальных тетрадей на каждый учеб­ный год в двух вариантах. При проведении самостоятельных работ ставится прежде всего цель выявить уровень математической подготовки детей и своевременно устранить имеющиеся пробелы знаний. В конце каждой само­стоятельной работы отведено место для работы над ошибками. На первых порах учитель должен помочь детям в выборе заданий, позволяющих свое­временно исправить допущенные ошибки. В течение года самостоятельные работы с исправленными ошибками собираются в папку, что помогает уча­щимся проследить свой путь в освоении знаний.

Итоговый контроль. Его главный показатель - решение задач в итого­вых контрольных работах. В отличие от самостоятельных работ, основная функция контрольных работ - это именно контроль знаний. С самых первых шагов ребенка следует учить быть во время контроля знаний особенно вни­мательным и точным в своих действиях. Результаты контрольной работы, как правило, не исправляются - к контролю знаний нужно готовиться до него, а не после.

Основной принцип проведения контроля знаний в Образовательной сис­теме «Школа XXI» - минимизация стресса детей. Атмосфера в классе долж­на быть спокойной и доброжелательной. Возможные ошибки в самостоя­тельной работе должны восприниматься не более, чем сигнал для их дора­ботки и устранения. Спокойная атмосфера во время контрольных работ оп­ределяется той большой подготовительной работой, которая проведена пред­варительно и которая снимает все поводы для беспокойства.

Во всех видах контроля надо руководствоваться двумя правилами:

1.Не следует торопиться выставить ученику низкую отметку или зафикси­ровать, что этими возможностями он еще не овладел. В случае если ученик выполнил задание неуспешно, лучше дать ему возможность выполнить рабо­ту над ошибками и выставлять отметку уже после выполнения этой работы.

2.Ученик должен иметь возможность пересдать, исправить не устраиваю­щую его отметку.

Авторы и методисты Образовательной системы «Школа XXI» предлагают дифференцировать качественную отметку через уровни успешности, где ка­ждый уровень - это степень сложности решаемых задач.

Необходимый уровень (нижний «мини» минимакса) - возможности (со­четание умений и знаний), ориентированные на требования государственного стандарта. Соответствие только им - это «хорошо», но не «отлично».

Программный уровень (верхний «мини» минимакса) - возможности (со­четание умений и знаний), соответствующие требования предметных про­грамм Образовательной системы «Школа XXI». Соответствие им - это «от­личный» показатель для школьника.

Максимальный уровень («макси») - возможности (сочетание умений и

знаний), превышающие требования школьной программы.

Пользоваться уровнями успешности необходимо начинать в начальной школе. Это способствует развитию умений самоконтроля и самооценки.

Сначала ученик учится определять успех или неуспех своей учебной дея­тельности и как только эта ступень будет пройдена, можно предложить уче­никам задуматься над тем, что задачи, которые они решают, отличаются друг от друга по сложности. Для начала можно условно делить их на «простые», «сложные» и «очень сложные», постепенно в диалоге с детьми определяя признаки каждого уровня. Когда умение дифференцировать оценку своих ус­пехов уже будет намечено, можно знакомить учеников собственно с уровня­ми успешности - например, так, как это сделано в «Дневнике школьника -XXI ».

Как известно, в традиционной системе обучения существует только одна жесткая пятибалльная система оценивания. В Образовательной системе «Школа XXI века», основанной на инициативности и творческом поиске каждого участника образовательного процесса, наблюдается сосуществование не­скольких вариантов выражения качественной оценки в виде отметки, каждый из которых может быть выбран учителем или педагогическим коллективом. Приведем несколько возможных вариантов выставления отметок.

Вариант наполнения «старой» пятибалльной системы новым содержани­ем, когда ученик сам по выбранным критериям выставляет себе «3», «4», «5». Очевидный плюс этого варианта в том, что он требует изменения системы отчетности. Очевидный минус - только три приемлемых балла не позволяет точно информировать ученика о степени его успешности.

Вариант фактически безотметочного обучения. В этом случае текущие ус­пехи ученика фиксируются в особом журнале, где в качестве граф указаны не уроки, а перечень возможных ЗУН-ов, которыми должен и может овладеть ученик. После получения соответствующих результатов в ходе диагностики (проверочных работ) в графах фиксируется овладение учеником данными возможностями (ставится «+»). Процент плюсов определит, на каком уровне ученик освоил возможности по данному предмету. Этот процент можно пе­реводить в официальные пятибалльные или любые другие отметки в конце учебного года или в конце учебной ступени.

Вариант замены традиционных пятибалльных отметок баллами успешно­сти. Он хорош для учителя-энтузиаста, готового самостоятельно (с разреше­ния администрации школы) отойти от пятибалльной системы. Соотношение между баллами успешности и пятибалльной системой такое:

Таблица 1

Соотношение между баллами успешности и пятибалльной системой.

Качественная оценка	Отметка - баллы ус­пешности (б.у.)	Пятибалльная от­метка
Не достигнут да­же минимальный уровень	Пустая клетка - незачет или «0» - долговое обя­зательство	2(двойка) или н/а (не аттестован). Возможно испра­вить!
Необходимый уровень (нижний «мини»)	1 б.у. - частичное ос­воение нижнего «ми­ни»	3 (тройка). Право исправить!
2 б.у. - полное освое­ние нижнего «мини»	4 (четверка). Право отказаться от выставления!
Программный уровень (верхний «мини»)	3 б.у. - частичное ос­воение верхнего «ми­ни».	4+ (четверка с плюсом)
4 б.у. - полное освое­ние верхнего «мини».	5 (пятерка).

Максимальный	5 б.у. - приближение к	5+ (пятерка с плю-
уровень («мак-	уровню «макси».	сом)
си»)
6 б.у. - выход на уровень «макси»)	5+ (пятерка с плюсом)

Указанные выше баллы успешности можно заносить в таблицу требова­ний и, не переводя их каждый раз в пятибалльную отметку, сразу по баллам успешности определять итоговую оценку или итоговую отметку. С уровнем успешности могут быть соотнесены и другие системы отметок: 10-бальная система, 100%-ный рейтинг, накопительные баллы и т.д.

Таким образом, можно выделить следующие особенности системы кон­троля результатов обучения младших школьников математике:

цель контроля результатов обучения - как ученик продвигается по предметным линиям развития личности;

определение качественного уровня задания и правильности его выпол­нения осуществляется по соглашению учителя и учеников;

дифференциация качественной отметки через уровни успеваемости;

наблюдается сосуществование нескольких вариантов выражения каче­ственной оценки в виде отметки.

Главной центральной и единственно осознаваемой целью образования является обучение конкретному предмету, вооружение учащихся суммой знаний-умений. При этом предполагается, что реализация такой цели сама по себе обеспечит решение задачи развития ребенка.

Разработчики проекта «Начальная школа 21 века» считали необходимым ответить на следующие вопросы:

1) Каковы приоритетные цели обучения в начальной школе? (целостное гармоничное развитие личности школьника, становление элементарной культуры деятельности, овладение основными компонентами учебной деятельности: умением принимать учебную задачу, определять учебные операции и т.д., формирование готовности к самообразованию)

2) Что такое развитие младшего школьника? ( развитие- сформированное умение использовать свои знания в нестандартных ситуациях; сформированное умение добывать знания, желание выполнять любую задачу творчески; сформированные умения осознавать свое незнание, находить причину сделанной ошибки; высокий уровень психических процессов)

3) Как нужно строить процесс обучения в первом школьном звене? (интеграция).

Список рекомендуемой литературы:

1. Беседы с учителем: Первый класс начальной школы. Под ред. Н. Ф. Виноградовой и Л. Е. Журовой. - М.: Издательский центр «Вентана-Граф». 1998. -240 с.

2. Беседы с учителем: Второй класс четырехлетней начальной школы / Под редю Л.Е.Журовой. –М.: Вента-граф, 1999,-320с.

3. Беседы с учителем: Третий класс четырехлетней начальной школы /Под ред. Л.Е.Журовой. –М.: Вента-граф, 2000, -384с.

4. Беседы с учителем: Методика обучения: Четвертый класс четырехлетней школы/ Под ред. Л.Е.Журовой. –М.: Вента-граф, 2001, -480с.

5. Беседы с учителем: Первый класс четырехлетней школы, Отвечаем на ваши письма: Вып. 1. - М.: Вентана-Граф, 2000. - 48 с,

6. Беседы с учителем: Первый, второй классы четырехлетней школы. Отвечаем на Ваши письма: Вып-2. –М.: Вента-раф, 2000, -48с.

7. Программы четырехлетней начальной школы

8. Проект "Начальная школа.XXI века" /Руководитель проекта Н.Ф. Виноградова. –М.: Вента-граф, 2001, -144с.

9. Концептуальные основы построения учебно-методического комплекса для первого звена школы / Сост. Н.Ф. Виноградова, Л.Е.Журова. Проект "Начальная школа XXI века" ~М.: Вентана-Граф, 2000. - 120с.

10. Рудницкая В. Н. Предмет «Математика» в начальной школе - М.: Ассоциация «Профессиональное образование», 1995 - 56 с.

11. Рудницкая В. Н, Математика. 1 кл. -М.: Вентана-Граф, 2000.

12. Рудницкая В. Н. Математика. Рабочая тетрадь К» 1. 2. 1 кл. -М.: Вентана-

13. Г^оА О А ПА

14. КочуроваЕ. 3, Я учусь считать. Рабочая тетрадь. 1 кл. -М.: Вентана-Граф, 2000.

15. Рудницкая В. Н.. Юдачева Т. В. Математика. 2 кл. -М.: Вентана-Граф, 2000.

16. Рудницкая В. Н.. Юдачева Т. В. Математика. Рабочая тетрадь № 1, 2. 2 кл. -М,: Вентана-Граф, 2000.

17. КочуроваЕ. Э. Дружим с математикой. Рабочая тетрадь. 2 кл. -М.: В ентана-Го аф. 2 0 00..

18. Рудницкая В. Н.. Юдачева Т. В. Математика. 3 кл. — М.: Вентана-Граф. 2000.

19. Рудницкая В. Н.. Юдачева Т. В. Математика. Рабочая тетрадь. Ч. Г 2. 3 кл.

20. — М.: Вентана-Гпаф. 2.000.

21. Рудницкая В, Н,, Юдачева Т. В. Математика. 4 кл. -М,: Вентана-Граф, 2000.

22. Рудницкая В. Н.. Рогачева Т. В. Математика. Рабочая тетрадь. Ч. I, 2. 4 кл.

23. — М.: Вентана-Граф, 2000.

24. КочуроваЕ.Э. Дружим: с математикой. 3 кл. Рабочая тетрадь. -М.:
Вентана-Граф, 2001.

25. Кочурова Е.Э. Дружим с математикой. 4кл. Рабочая тетрадь. –М.: Вента-граф, 2000.

26. 22. Рудницкая В.Н. Я иду на урок в начальную школу: 1-4 классы: Тесты по математике._М.: Издательство «Первое сентября», 2002.