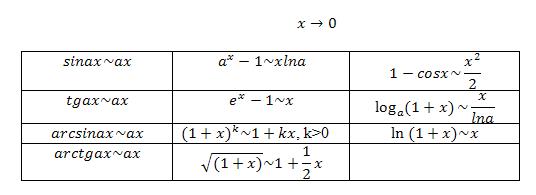Определение предела функции. Критерий Коши существования предела функций

Ответ:

Первое определение предела функции

Это определение часто называют определением предела функции по Гейне.

Точка a называется пределом функции 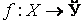в точке x0 (или, что то же, при x®x0), если для любой последовательности xnÎX, имеющей своим пределом точку x0, т. е. такой, что

,

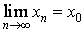последовательность 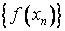имеет своим пределом точку a, т. е.

.

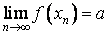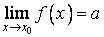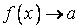В том случае, когда a является пределом функции f в точке x0, пишут или при .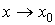

Определение предела при заданной функции 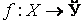содержательно только тогда, когда для точки x0 действительно существуют последовательности точек xnÎX, имеющие своим пределом (конечным или бесконечным) точку x0: .

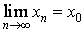Пусть XÌ¡. Точка x0, для которой существует последовательность xnÎX, имеющая своим пределом точку x0, называется точкой прикосновения множества X.

Очевидно, что любая точка x0, принадлежащая самому множеству X, является его точкой прикосновения, так как стационарная последовательность x0 = xnÎX удовлетворяет условиям данного определения: 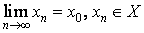. Но, безусловно, у множеств могут существовать и конечные точки прикосновения, не принадлежащие этим множествам. Так, например, точки x=a и x=b являются точками прикосновения интервала (a, b) и не содержатся в нём.

Существует другое определение предела функции, не использующее понятие предела последовательности, а формулируемое в терминах окрестностей и называемое определением предела функции по Коши.

Сформулируем сначала определение конечного предела в конечной точке.

Число a называется пределом функции f в точке x0Ρ, если для любого e > 0 существует такое d = d(e)>0, что для всех x, удовлетворяющих условиям 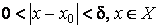, выполняется неравенство .

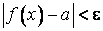Такую формулировку определения предела функции называют формулировкой на «языке e-d».

Бесконечные пределы в точке x0 на языке e-d определяются следующим образом: +¥ (–¥) называется пределом функции f в точке 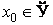, если для любого e>0 существует такое d = d(e) > 0 , что для всех x, удовлетворяющих условиям 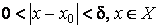, выполняется неравенство ( ).

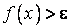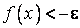Аналогичным образом определяется предел функции в бесконечно удалённых точках.

Если функция f непрерывна в точке 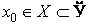, то определение непрерывности в символической записи имеет вид:

.

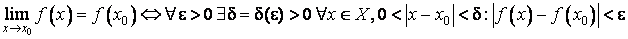Эквивалентные бесконечно малые. Таблица эквивалентностей.

Ответ:

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .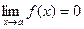

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .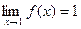

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где

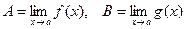, тогда

f(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит

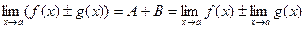
Теорема доказана.

Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где

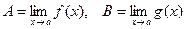, тогда

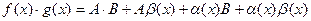
A×B = const, a(х) и b(х) – бесконечно малые, значит

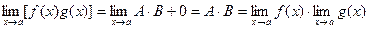
Теорема доказана.

Таблица эквивалентностей: