Уравнение касательной плоскости и нормали к поверхности
Рассмотрим геометрические приложения производной функции нескольких переменных. Пусть функция двух переменных задана неявно: 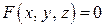 . Эта функция в области своего определения изображается некоторой поверхностью (п. 5.1). Возьмем на данной поверхности произвольную точку
. Эта функция в области своего определения изображается некоторой поверхностью (п. 5.1). Возьмем на данной поверхности произвольную точку 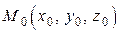 , в которой все три частных производных
, в которой все три частных производных 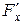 ,
, 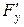 ,
, 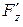 существуют и непрерывны, причем хотя бы одна из них не равна нулю.
существуют и непрерывны, причем хотя бы одна из них не равна нулю.
Точка с такими характеристиками называется обыкновенной точкой поверхности. Если хотя бы одно из указанных выше требований не выполняется, то точка называется особой точкой поверхности.
Через выбранную на поверхности точку можно провести множество кривых, к каждой из которых может быть проведена касательная.
Определение 5.8.1. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через некоторую точку 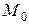 , называется касательной плоскостью к данной поверхности в точке
, называется касательной плоскостью к данной поверхности в точке 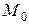 .
.
Чтобы провести данную плоскость достаточно иметь две касательных прямых, то есть две кривых на поверхности. Это могут быть кривые, полученные в результате сечения данной поверхности плоскостями 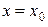 ,
, 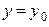 (рис. 5.8.1).
(рис. 5.8.1).
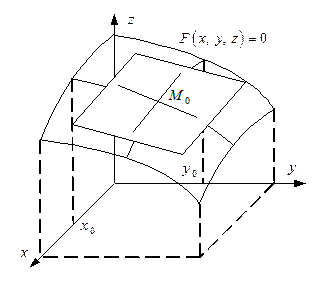
Рис. 5.8.1
Запишем уравнение касательной линии к кривой, лежащей на пересечении поверхности 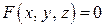 и плоскости
и плоскости 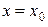 . Поскольку данная кривая лежит в системе координат
. Поскольку данная кривая лежит в системе координат 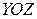 , то уравнение касательной к ней в точке
, то уравнение касательной к ней в точке 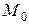 , в соответствии с п. 2.7, имеет вид:
, в соответствии с п. 2.7, имеет вид:
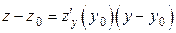 . (5.8.1)
. (5.8.1)
Соответственно, уравнение касательной к кривой, лежащей на пересечении поверхности и плоскости 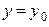 , в системе координат
, в системе координат 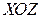 в той же точке имеет вид:
в той же точке имеет вид:
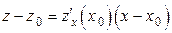 . (5.8.2)
. (5.8.2)
Воспользуемся выражением для производной неявно заданной функции (п. 5.7). Тогда 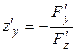 , а
, а 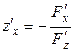 . Подставляя эти производные в (5.8.1) и (5.8.2), получим, соответственно:
. Подставляя эти производные в (5.8.1) и (5.8.2), получим, соответственно:
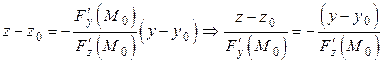 ; (5.8.3)
; (5.8.3)
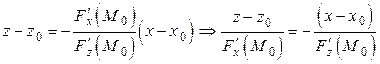 . (5.8.4)
. (5.8.4)
Поскольку полученные выражения не что иное, как уравнения прямых в канонической форме (п. 15), то из (5.8.3) получаем направляющий вектор 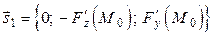 , а из (5.8.4) –
, а из (5.8.4) – 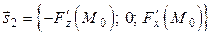 . Векторное произведение
. Векторное произведение 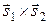 даст вектор, нормальный к данным касательным линиям, а, следовательно, и к касательной плоскости:
даст вектор, нормальный к данным касательным линиям, а, следовательно, и к касательной плоскости:
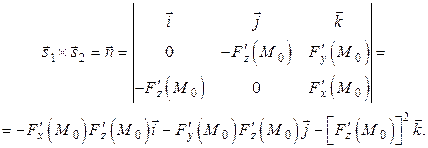
Отсюда следует, что уравнение касательной плоскости к поверхности 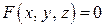 в точке
в точке 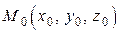 имеет вид (п. 14):
имеет вид (п. 14):
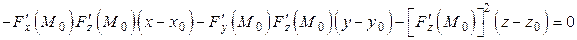
или
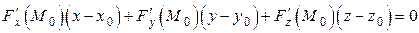 .
.
Определение 5.8.2. Прямая, проведенная через точку 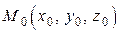 поверхности
поверхности 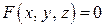 перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности.
перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности.
Так как направляющий вектор нормали к поверхности совпадает с нормалью к касательной плоскости 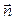 , то уравнение нормали имеет вид:
, то уравнение нормали имеет вид:
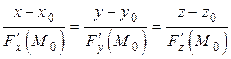 .
.
Скалярное поле
Пусть в пространстве задана область 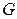 , занимающая часть или все это пространство. Пусть каждой точке этой области по какому-то закону поставлена в соответствие некоторая скалярная величина (число).
, занимающая часть или все это пространство. Пусть каждой точке этой области по какому-то закону поставлена в соответствие некоторая скалярная величина (число).
Определение 5.9.1. Область в пространстве, каждой точке которой 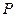 ставится в соответствие по известному закону некоторая скалярная величина
ставится в соответствие по известному закону некоторая скалярная величина 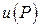 , называется скалярным полем.
, называется скалярным полем.
Если с областью 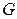 связана какая-то система координат, например, прямоугольная декартовая, то каждая точка приобретает свои координаты. В этом случае скалярная величина
связана какая-то система координат, например, прямоугольная декартовая, то каждая точка приобретает свои координаты. В этом случае скалярная величина 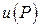 становится функцией координат: на плоскости –
становится функцией координат: на плоскости – 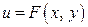 , в трехмерном пространстве –
, в трехмерном пространстве – 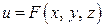 . Скалярным полем часто называют и саму функцию
. Скалярным полем часто называют и саму функцию 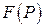 , описывающую данное поле. В зависимости от размерности пространства, скалярное поле может быть плоским, трехмерным и т.д.
, описывающую данное поле. В зависимости от размерности пространства, скалярное поле может быть плоским, трехмерным и т.д.
Необходимо подчеркнуть, что величина скалярного поля зависит лишь от положения точки 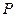 в области
в области 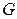 , но не зависит от выбора системы координат.
, но не зависит от выбора системы координат.
Определение 5.9.2. Скалярное поле, зависящее только от положения точки 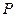 в области
в области 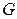 , но не зависящее от времени, называется стационарным.
, но не зависящее от времени, называется стационарным.
Нестационарные скалярные поля, то есть зависящие от времени, в данном разделе нами рассматриваться не будут.
В качестве примеров скалярных полей можно назвать поле температур, поле давлений в атмосфере, поле высот над уровнем океана.
Геометрически скалярные поля часто изображаются с помощью так называемых линий или поверхностей уровня.
Определение 5.9.3. Множество всех точек пространства, в которых скалярное поле 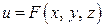 имеет одно и то же значение
имеет одно и то же значение 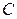 называется поверхностью уровня или эквипотенциальной поверхностью. В плоском случае для скалярного поля
называется поверхностью уровня или эквипотенциальной поверхностью. В плоском случае для скалярного поля 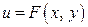 это множество называется линией уровня или эквипотенциальной линией.
это множество называется линией уровня или эквипотенциальной линией.
Очевидно, что уравнение поверхности уровня имеет вид 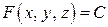 , линии уровня –
, линии уровня – 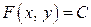 . Придавая в данных уравнениях константе
. Придавая в данных уравнениях константе 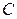 разные значения, получаем семейство поверхностей или линий уровня. Например,
разные значения, получаем семейство поверхностей или линий уровня. Например, 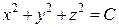 (вложенные друг в друга сферы с разными радиусами) или
(вложенные друг в друга сферы с разными радиусами) или 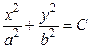 (семейство эллипсов).
(семейство эллипсов).
В качестве примеров линий уровня из физики можно привести изотермы (линии равных температур), изобары (линии равных давлений); из геодезии – линии равных высот и т.д.
