Квадратурная формула гаусса
Квадратурная формула Гаусса на первый взгляд похожа на формулу Чебышева
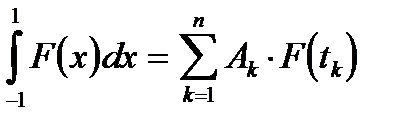 . (2.18)
. (2.18)
Только Гаусс для своей формулы предложил другое условие: Квадратурная формула (2.18) точна для всех полиномов максимально возможной степени M.
В формуле (2.18) насчитывается 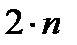 неизвестных -
неизвестных - 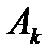 и
и 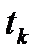 . Для их единственного определения нам необходимо иметь
. Для их единственного определения нам необходимо иметь 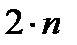 уравнений.
уравнений.
Если подставить полиномы 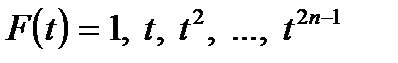 в формулу (2.18), мы получим недостающие
в формулу (2.18), мы получим недостающие 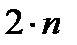 уравнений:
уравнений:
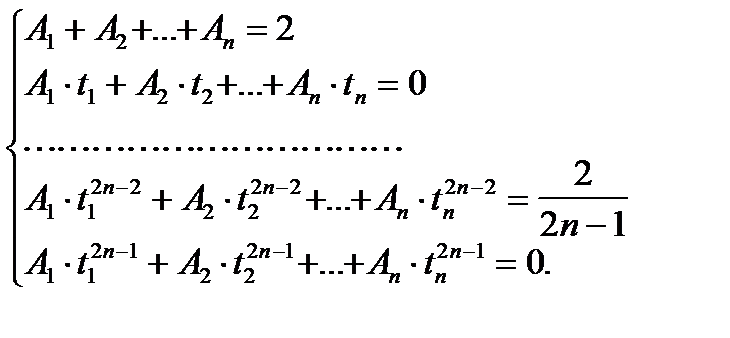 . (2.19)
. (2.19)
Система (2.19) является нелинейной, ее можно решить с помощью полиномов Лежандра. Решение данной системы - коэффициенты 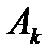 и
и 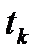 даны в таблице:
даны в таблице:
| n | k | tk | Ak |
| 1; 2 | 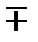 0.57735027 0.57735027 | ||
| 1; 3 | 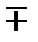 0.77459667 0.77459667 | 0.55555556 0.88888889 | |
| 1; 4 2; 3 | 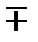 0.86113631 0.86113631 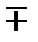 0.33998104 0.33998104 | 0.34785484 0.65214516 | |
| 1; 5 2; 4 | 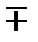 0.90617985 0.90617985 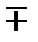 0.53846931 0.53846931 | 0.23692688 0.47862868 0.56888889 | |
| 1; 6 2; 5 3; 4 | 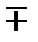 0.93246951 0.93246951 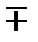 0.66120939 0.66120939 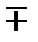 0.23861919 0.23861919 | 0.17132450 0.36076158 0.46791394 | |
| 1; 7 2; 6 3; 5 | 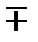 0.94910791 0.94910791 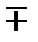 0.74153119 0.74153119 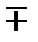 0.40584515 0.40584515 | 0.12948496 0.27970540 0.38183006 0.41795918 | |
| 1; 8 2; 7 3; 6 4; 5 | 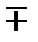 0.96028986 0.96028986 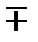 0.79666648 0.79666648 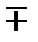 0.52553242 0.52553242 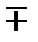 0.18343464 0.18343464 | 0.10122854 0.22238104 0.31370664 0.36268378 |
Для вычисления общего интеграла
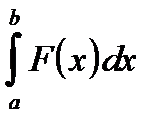
применяют замену переменных
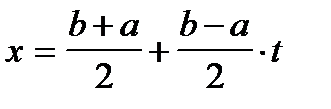 .
.
В результате квадратурная формула Гаусса имеет вид:
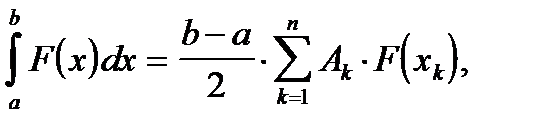 (2.20)
(2.20)
где
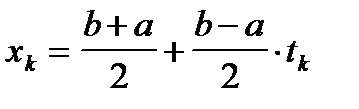 . (2.21)
. (2.21)
Т.о. формула Гаусса является более точной по сравнению с формулой Чебышева и позволяет вычислять точное значение интеграла для полиномов степени 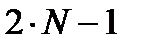 (т.е. 15 степени по сравнению с 9 степенью формулы Чебышева).
(т.е. 15 степени по сравнению с 9 степенью формулы Чебышева).
Методы решения СЛАУ
Постановка задачи
Пусть дана система n уравнений с n неизвестными:
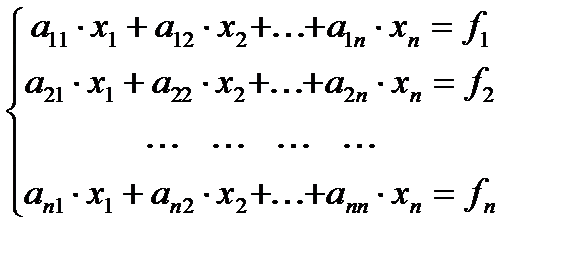 . (3.1)
. (3.1)
В дальнейшем будем записывать ее в виде
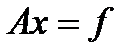 , где
, где 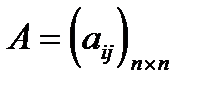 ,
, 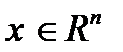 ,
, 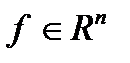 . (3.2)
. (3.2)
Методы решения систем линейных алгебраических уравнений (СЛАУ) делятся на две группы: точные и итерационные.
Под точными методами подразумеваются методы, которые дают решение задачи при помощи конечного числа элементарных арифметических операций. При этом, если исходные данные, определяющие задачу, заданы точно и вычисления производились точно, то решение также получается точным. К сожалению, при работе ЭВМ с вещественными числами возникают ошибки округления, которые снижают точность результатов.
Итерационные методы состоят в том, что решение системы (3.1) находится как предел при 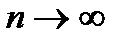 последовательных приближений
последовательных приближений 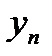 , где
, где 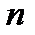 - номер итерации. Как правило, за конечное число итераций предел не достигается. Обычно задается некоторое число
- номер итерации. Как правило, за конечное число итераций предел не достигается. Обычно задается некоторое число 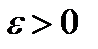 (погрешность) и вычисления проводятся до тех пор, пока не будет выполнена оценка
(погрешность) и вычисления проводятся до тех пор, пока не будет выполнена оценка 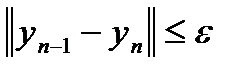 .
.
Выбор метода из списка существующих производится в соответствии с
· Размерностью задачи. Прямые методы используют для задач при 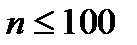 , при больших
, при больших 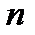 применяют итерационные методы.
применяют итерационные методы.
· Характером матрицы. Существует несколько типов матриц, таких как симметричные матрицы, положительно определенные матрицы, треугольные матрицы и т.д. В зависимости от типа матрицы задачи используют различные численные методы.
· Объемом памяти и быстродействием ЭВМ. На ЭВМ с большим объемом памяти используют методы, которые требуют много памяти, но и решение задачи получается быстрым. Для ЭВМ с высоким быстродействием применяют методы с большим количеством вычислений, но с меньшими требованиями к размеру оперативной памяти.
К решению систем СЛАУ приводится подавляющее большинство задач вычислительной математики. В настоящее время известно большое количество алгоритмов решения задач линейной алгебры, большинство из которых рассчитано на матрицы 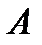 специального вида (трехдиагональные, симметричные, большой разряженности и т.д.).
специального вида (трехдиагональные, симметричные, большой разряженности и т.д.).
Сопоставление между собой прямых методов проводится обычно по числу арифметических действий, необходимых для получения решения. При прочих равных условиях предпочтение отдается методу с меньшим числом операций. Например, для метода Гаусса требуется порядка 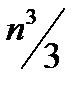 действий, а для метода Крамера порядка
действий, а для метода Крамера порядка 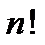 операций.
операций.
При применении итерационных методов существенным является не только сходимость итерационного процесса, но и быстрота сходимости. В этом отношении каждый итерационный метод не является универсальным. Давая быструю сходимость для одного типа матриц, он может сходиться медленно или вообще не сходиться для других матриц.
Ниже будут представлены прямые методы - метод Крамера, варианты метода Гаусса и схема Халецкого, и итерационные методы - метод Якоби, Зейделя, верхней релаксации и метод итераций.
Метод Крамера
Метод Крамера является одним из самых известных методов алгебры. Вначале дадим определение: Матрица 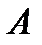 называется невырожденной матрицей, если ее определитель
называется невырожденной матрицей, если ее определитель 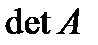 не равен нулю. В этом случае, в соответствии с методом Крамера, существует единственное решение
не равен нулю. В этом случае, в соответствии с методом Крамера, существует единственное решение
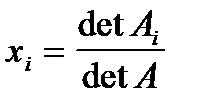 ,
, 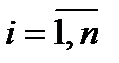 ,
,
где матрица 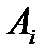 получается из матрицы
получается из матрицы 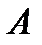 заменой столбца i на столбец свободных членов F.
заменой столбца i на столбец свободных членов F.
Формула Крамера дает решение уравнения в явном виде, но с вычислительной точки зрения она невыгодна. Расчет по ней требует слишком большого числа операций и оказывается очень чувствительным к ошибкам округления. Поэтому на практике при вычислениях на компьютерах используют другие методы. Автор использует формулу Крамера для решения систем уравнений с двумя неизвестными, что возможно выполнить «в уме».
Метод Гаусса
Метод Гаусса является универсальным и эффективным прямым методом решения систем линейных алгебраических уравнений. У метода Гаусса существует несколько вариантов. Наиболее распространенный вариант называется схемой единственного деления или методом последовательного исключения неизвестных. Также его называют методом Гаусса без выбора главного элемента. Ниже будут рассмотрены варианты метода Гаусса без выбора главного элемента, с выбором главного элемента по строкам, столбцам и матрице.
Метод Гаусса выполняется в два этапа:
Þ Прямой ход. Система уравнений приводится к треугольному виду.
Þ Обратный ход. Заключается в последовательном определении неизвестных из полученной треугольной системы.
Итак, решение системы уравнений (3.1) по схеме единственного деления заключается в следующем:
Предположим, что коэффициент 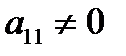 . Разделим коэффициенты первого уравнения системы (3.1) на
. Разделим коэффициенты первого уравнения системы (3.1) на 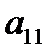 . Первое уравнение примет вид:
. Первое уравнение примет вид:
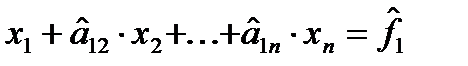 , (3.3)
, (3.3)
где
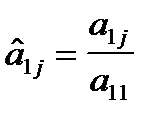 для
для 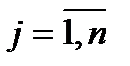 и
и 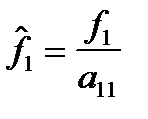 .
.
Используя уравнение (3.3), можно исключить из системы (3.1) неизвестную 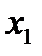 (везде, кроме первого уравнения). Для этого вычтем из второго уравнения системы уравнение (3.3), умноженное на
(везде, кроме первого уравнения). Для этого вычтем из второго уравнения системы уравнение (3.3), умноженное на 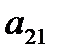 . Далее, из третьего уравнения вычтем уравнение (3.3), умноженное на
. Далее, из третьего уравнения вычтем уравнение (3.3), умноженное на 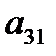 и т.д. В результате получим следующую систему
и т.д. В результате получим следующую систему
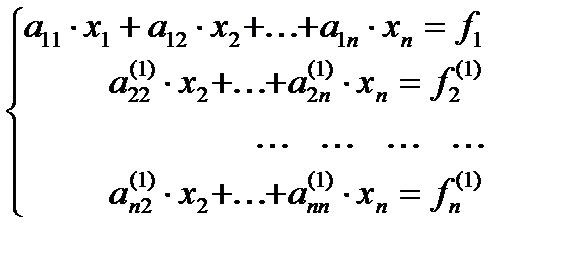 , (3.4)
, (3.4)
где коэффициенты 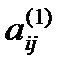 и
и 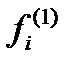 для
для 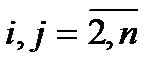 вычисляются по формулам
вычисляются по формулам
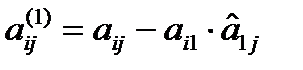 и
и 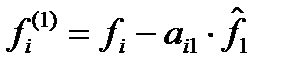 .
.
Предполагаем, что коэффициент 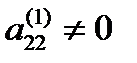 и аналогичным способом исключаем из системы (3.4) неизвестную
и аналогичным способом исключаем из системы (3.4) неизвестную 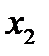 (кроме первого и второго уравнения). Далее избавляемся от неизвестного
(кроме первого и второго уравнения). Далее избавляемся от неизвестного 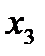 и т.д. В результате получаем следующую систему уравнений
и т.д. В результате получаем следующую систему уравнений
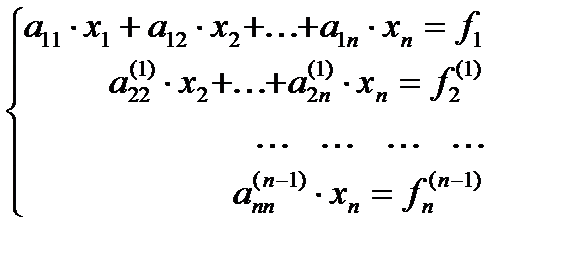 , (3.5)
, (3.5)
Итак, в результате выполнения первого этапа метода Гаусса - прямого хода - от системы уравнений (3.1) переходим к эквивалентной ей системе уравнений (3.5) с треугольной матрицей. Как известно, решение системы уравнений с треугольной матрицей является достаточно простой операцией и выполняется по следующим формулам:
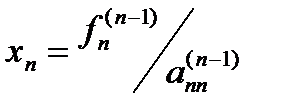 ,
,
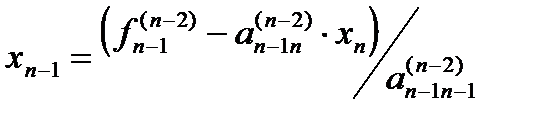 и т.д.
и т.д.
Общая формула имеет вид:
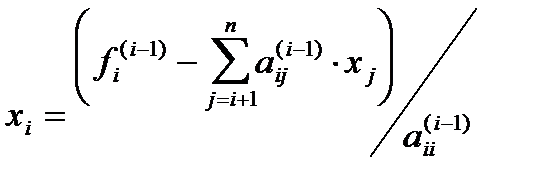 , (3.6)
, (3.6)
где 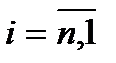 .
.
Примечание. При 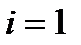 имеем
имеем 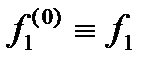 и
и 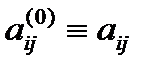 .
.
Коэффициенты, стоящие на главной диагонали системы (3.5) - 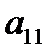 ,
, 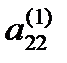 , ...,
, ..., 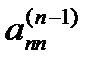 , - называются главными (или ведущими) элементами. Систему уравнений можно решить методом Гаусса, если все ее главные элементы отличны от нуля. В противном случае система единственного решения не имеет. Поэтому при исключении неизвестных на первом этапе рекомендуется проверить главный элемент текущего уравнения на равенство нулю.
, - называются главными (или ведущими) элементами. Систему уравнений можно решить методом Гаусса, если все ее главные элементы отличны от нуля. В противном случае система единственного решения не имеет. Поэтому при исключении неизвестных на первом этапе рекомендуется проверить главный элемент текущего уравнения на равенство нулю.
Метод Гаусса является точным методом и теоретически дает точное решение системы уравнений (3.1). На практике методом Гаусса можно получить только приближенное решение. При вычислениях на компьютерах возникают ошибки округления, которые понижают точность вычислений.
Пример. Решить систему уравнений схемой единственного деления. При вычислениях все числа округлять до пяти цифр. Пример показывает, как ошибки округления могут привести к получению неверного решения.
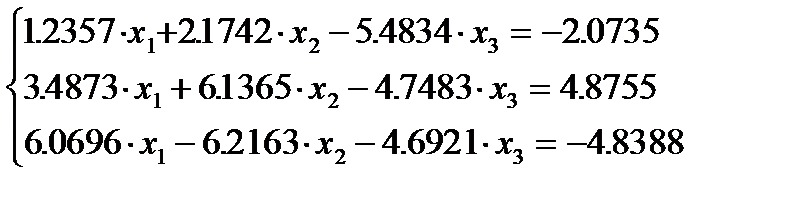 .
.
Исключили неизвестную 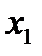 и получили систему
и получили систему
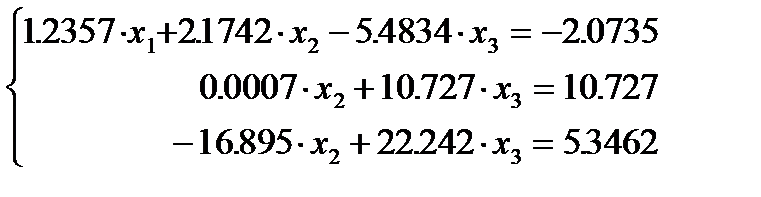 .
.
Исключаем неизвестную 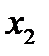 :
:
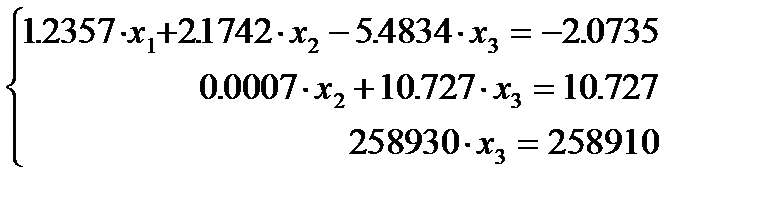
Прямой ход закончился. Выполняем второй этап и получаем следующее решение:
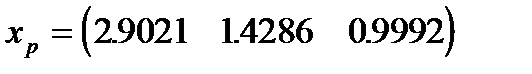 ,
,
в то время как точное решение имеет вид:
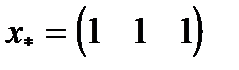 .
.
На примере видно, что небольшая погрешность для 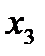 , равная 0.0008, стремительно увеличивается для
, равная 0.0008, стремительно увеличивается для 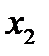 до 0.4286 и достигает максимума для
до 0.4286 и достигает максимума для 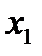 (1.9021).
(1.9021).
Итак, приближенное решение 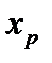 почти в три раза больше точного решения
почти в три раза больше точного решения 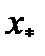 . Данное возмущение связано со вторым уравнением. Главный элемент второго уравнения равен 0.0007. В соответствии с формулой (3.6) погрешность решения
. Данное возмущение связано со вторым уравнением. Главный элемент второго уравнения равен 0.0007. В соответствии с формулой (3.6) погрешность решения 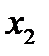 увеличилась в
увеличилась в 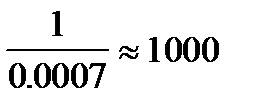 раз.
раз.
Если бы вычисления проводились без ошибок округления, то решение было бы точным. Но к сожалению, все расчеты с вещественными числами выполняются только приближенно. В зависимости от типа вещественного числа (Real, Single, Extended и т.д.) точными являются 10-20 знаков.
Вычислительную погрешность можно существенно уменьшить. Причина резкого роста погрешности заключена в малости ведущего элемента. Чтобы повысить точность метода, необходимо выбрать другой ведущий элемент. Существует несколько вариантов выбора главного элемента - по строкам, по столбцам и по матрице. Пусть необходимо исключить неизвестную 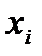 , т.е. работаем с i-тым уравнением. Выберем максимальный по модулю коэффициент в i-том столбце, из числа стоящих на главной диагонали и ниже. Пусть это будет коэффициент из j-того уравнения. Поменяем местами уравнения № i и j. Продолжим исключение неизвестных. Описанный алгоритм и есть метод Гаусса с выбором главного элемента по столбцам. Если максимальный по модулю элемент будем искать в i-той строке, то получим метод Гаусса с выбором главного элемента по строкам. При выборе главного элемента в матрице поиск осуществляется в матрице коэффициентов - в строках от i до n и столбцах от i от n.
, т.е. работаем с i-тым уравнением. Выберем максимальный по модулю коэффициент в i-том столбце, из числа стоящих на главной диагонали и ниже. Пусть это будет коэффициент из j-того уравнения. Поменяем местами уравнения № i и j. Продолжим исключение неизвестных. Описанный алгоритм и есть метод Гаусса с выбором главного элемента по столбцам. Если максимальный по модулю элемент будем искать в i-той строке, то получим метод Гаусса с выбором главного элемента по строкам. При выборе главного элемента в матрице поиск осуществляется в матрице коэффициентов - в строках от i до n и столбцах от i от n.
В вышеописанном примере для исключения неизвестного 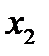 применим выбор главного элемента по столбцам. Ведущий элемент будет равен -16.895. В результате получим приближенное решение
применим выбор главного элемента по столбцам. Ведущий элемент будет равен -16.895. В результате получим приближенное решение
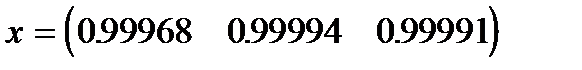 .
.
Следовательно, несмотря на ошибки округления, погрешность решения не превысила 0.0003
Пример. Ниже будет приведен фрагмент программы, реализующий прямой ход метода Гаусса без выбора главного элемента. Предполагается, что все необходимые переменные были определены ранее.
{Перебираем номера неизвестных k от первого до}
{предпоследнего. Будем исключать неизвестную x[k]}
For k:=1 to N-1 do
begin
{Если главный элемент равен нулю, даем}
{сообщение и завершаем работу программы}
If Abs(A[k,k])<0.001 then
begin
Writeln(’Главный элемент равен нулю.’);
Writeln(’Данную схему применять нельзя.’);
Halt(1);
end;
{Перебираем уравнения от k+1 до последнего}
For i:=k+1 to N do
begin
{Перебираем коэффициенты уравнения}
For j:=k+1 to N do
{и вычисляем их новые значения}
A[i,j]:=A[i,j]-A[i,k]*A[k,j]/A[k,k];
{Вычисляем значение коэфф. правой части}
F[i]:=F[i]-A[i,k]*F[k]/A[k,k];
end;
end;
Для получения решения системы уравнений применяется формула (3.6). Алгоритм вкратце выглядит следующим образом. Осуществляют перебор номеров i от n do 1. Вычисляют выражение, стоящее в скобках, обращая внимание на правильность суммирования, и значение дроби.
Примечание. На практике, если есть возможность выбора, рекомендуется использовать алгоритм выбора главного элемента по столбцам. При работе с вариантами выбора по строкам и матрице необходимо менять местами коэффициенты одного уравнения для разных неизвестных 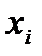 и
и 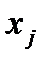 . Следовательно, меняется местоположение неизвестных. Полученная треугольная система уравнений не будет эквивалентна исходной. В результате полученное решение не будет решением поставленной задачи, т.к. элементы вектора решения будут перемешаны. Поэтому в алгоритмы выбора главного элемента по строкам и матрице добавляются новые команды восстановления решения.
. Следовательно, меняется местоположение неизвестных. Полученная треугольная система уравнений не будет эквивалентна исходной. В результате полученное решение не будет решением поставленной задачи, т.к. элементы вектора решения будут перемешаны. Поэтому в алгоритмы выбора главного элемента по строкам и матрице добавляются новые команды восстановления решения.
Пример. В программе метода Гаусса с выбором главного элемента по строкам и матрице для восстановления решения может использоваться нижеприведенный код.
{В массиве Por хранится информация о }
{местоположении элементов решения}
Var Por:Array[1..N] of Integer;
...
{После ввода коэфф. системы, задаем массив Por}
For i:=1 to N do Por[i]:=i;
...
{Пусть на I-том шаге исключения главный}
{элемент находится в j-том столбце.}
{Необходимо поменять местами коэффициенты }
{i и j столбца. Изменяем соответственно данные}
{в массиве Por. Для этого используем}
{переменную Vsp типа Integer}
Vsp:=Por[i]; Por[i]:=Por[j]; por[j]:=Vsp;
...
{Решили систему уравнений, далее требуется}
{восстановить решение. Полученное решение было}
{записано в массив X.}
{Восстановленное решение запишем в массив Xnew}
For i:=1 to N do
Xnew[i]:=X[Por[i]];
