Наличие обратного элемента

5. Подгруппа ― подмножество 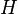группы 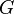, само являющееся группой относительно операции, определяющей .

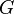Примеры:

Подмножество группы 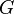, состоящее из одного элемента , будет, очевидно, подгруппой, и эта подгруппа называется единичной подгруппой группы .

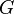Сама 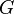также является своей подгруппой.

Полугруппой называют множество с заданной на нем ассоциативной бинарной операцией .

Примеры:

· Положительные целые числа с операцией сложения.

· Любая группа является также и полугруппой.

· Идеал кольца всегда является полугруппой относительно операции умножения.

· Множество всех отображений множества в себя с операцией суперпозиции отображений

· Множество всех бинарных отношений на множестве с операцией умножения бинарных отношений.

· Множество всех слов над некоторым алфавитом с операцией конкатенации (присоединения)

Две полугруппы S и T называются изоморфными, если существует биекция f : S → T, такая что .

6. Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение).

Область целостности (или целостное кольцо, или область цельности или просто область) — понятие общей алгебры: ассоциативное коммутативное кольцо без делителя нуля (произведение ненулевых элементов не равно 0).

7. Свойства колец:

1. — коммутативность сложения;

2. — ассоциативность сложения;

3. — существование нейтрального элемента относительно сложения;

4. — существование противоположного элемента относительно сложения;

5. — ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы^[1])

6. — дистрибутивность.

8. Подкольцо кольца — это пара , где — кольцо, а — мономорфизм (вложение) колец.

9. По́ле в общей алгебре — множество F с двумя бинарными операциями (аддитивная операция, или сложение) и (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образуеткоммутативное ассоциативное кольцо c единицей , все ненулевые элементы которого обратимы.

Примеры полей:

· — рациональные числа,

· — вещественные числа,

· — комплексные числа,

10. Свойства полей:

· Характеристика поля всегда или простое число.

· Поле характеристики содержит подполе, изоморфное полю рациональных чисел .

· Поле простой характеристики содержит подполе, изоморфное полю вычетов .

· Количество элементов в конечном поле всегда равно — степени простого числа.

· При этом для любого числа вида существует единственное (с точностью до изоморфизма) поле из элементов, обычно обозначаемое .

· Любой ненулевой гомоморфизм полей является вложением.

· В поле нет делителей нуля.

11. Подполем поля называется подмножество, которое само является полем относительно операций сложения и умножения, заданных в .

12. Булевой алгеброй^[1][2][3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:

		ассоциативность
		коммутативность
		законы поглощения
		дистрибутивность
		дополнительность