Випадок незалежних частинних похибок
У випадку незалежних частинних похибок коефіцієнт кореляції дорівнює нулю 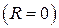 , і тоді формулу (2.5) для випадку, коли
, і тоді формулу (2.5) для випадку, коли 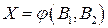 , залишімо у вигляді
, залишімо у вигляді
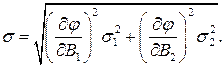
Цей висновок можна поширити й на більшу кількість величин 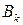 .
.
У загальному випадку, коли
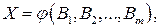
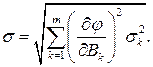 (2.7)
(2.7)
Таким чином, знаючи середньоквадратичні похибки прямих вимірювань за формулою (2.7), можна розрахувати середньоквадратичну похибку результатів непрямих вимірювань.
За формулою (2.7) можна обчислювати й граничні (максимальні) похибки. Дійсно, якщо закон розподілу усіх 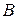 однаковий і задана однакова надійна ймовірність (при великому
однаковий і задана однакова надійна ймовірність (при великому 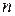 ), то і
), то і 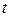 (коефіцієнт Стьюдента) однакові для усіх
(коефіцієнт Стьюдента) однакові для усіх 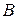 . Тоді максимальна похибка
. Тоді максимальна похибка
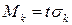
і
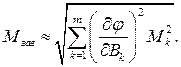 (2.8)
(2.8)
Розгляньмо деякі окремі випадки застосування формули (2.7).
а) Функціональну залежність між непрямими й безпосередньо вимірюваними величинами записують у вигляді
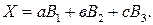
У цьому випадку
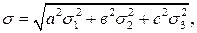
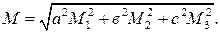
Приклад 1.Визначити максимальну похибку сумарного опору, складеного з 12 послідовно увімкнених опорів (2 опори по 1000±10 Ом; 4 опори по 100±3 Ом і 6 опорів по 10±1 Ом):
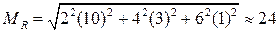 Ом;
Ом;
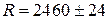 Ом .
Ом .
б) Функціональну залежність між непрямими й безпосередньо вимірюваними величинами виражають формулою, зручною для логарифмування:
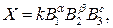
де
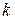 - числовий безрозмірний коефіцієнт;
- числовий безрозмірний коефіцієнт;
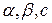 - постійні числа.
- постійні числа.
У тому випадку, коли в цю формулу входять різнорідні величини, розрахунок дисперсії результату непрямого вимірювання зручно робити, уводячи так звану відносну середньоквадратичну похибку. Покажімо це.
Визначімо частинні похідні
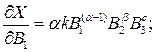
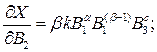
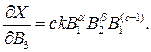
Тоді
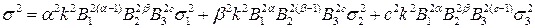 .
.
Розділивши обидві частини отриманого виразу на 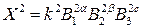 , одержимо
, одержимо
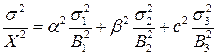
чи
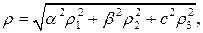
де
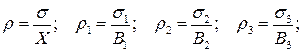
– відповідні відносні середньоквадратичні похибки.
У випадку, якщо відомі максимальні похибки, максимальна відносна похибка результату непрямого вимірювання визначається за формулою
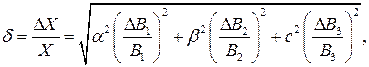
де 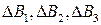 – максимальні похибки величин
– максимальні похибки величин 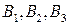 відповідно.
відповідно.
У випадку, якщо 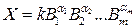 , одержимо
, одержимо
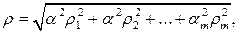
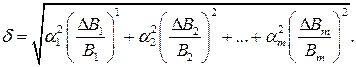
Приклад 2. Визначити відносну середньоквадратичну похибку непрямого вимірювання власної частоти резонансного контуру, якщо величини 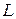 і
і 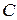 вимірювані з відносними середньоквадратичними похибками 2,5% і 1,5% відповідно
вимірювані з відносними середньоквадратичними похибками 2,5% і 1,5% відповідно
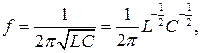
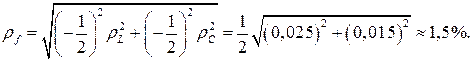
Приклад 3.Знайти значення максимальної похибки вимірювання електричної енергії з наступними даними:
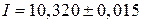 А;
А;
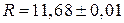 Ом;
Ом;
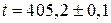 с.
с.
Для обчислення енергії скористуймося формулою
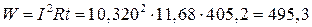 кДж.
кДж.
Відносна максимальна похибка непрямого вимірювання енергії
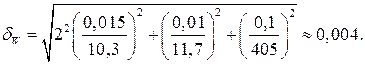
Отже, максимальна похибка визначення енергії
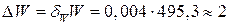 кДж.
кДж.
Остаточно 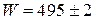 кДж.
кДж.
