Свойства двойных интегралов

Задача, приводящая к понятию двойного интеграла.

Предположим, что на 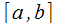определена функция 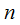частей 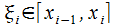и запишем сумму

(17.1)

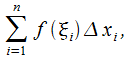
которая именуется интегральной.

О: Под определенным интегралом (о.и.) от функции 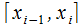и от выбора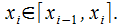

Обозначение: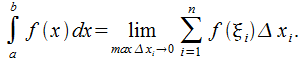

Числа 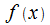именуют интегрируемой (по Риману) на .

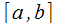Т. существования: При условии, что .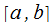

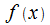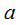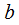В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида , пределов и , однако не зависит от символа обозначения переменной 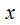, иначе выражаясь

(17.2)

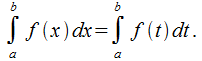
В соответствии с п.17.1.1 и 17.1.2 и определением о.и. запишем формулы площади криволинейной трапеции: 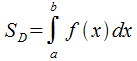, работы силы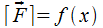

на :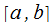

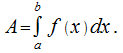
Понятие двойного интеграла, интегральных сумм.

Существование двойного интеграла, т. е. предела интегральной суммы для кажется очевидным, так как этот предел дает объем цилиндрического тела. Однако это рассуждение не является строгим. В более полных курсах это утверждение строго доказывается и носит название теоремы существования двойного интеграла.

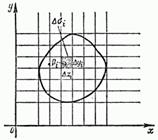
Рис. 230

Теорема существования. Для всякой функции , непрерывной в ограниченной замкнутой области, имеющей площадь а, существует двойной интеграл, т. е. существует предел интегральных сумм при неограниченном увеличении числа малых площадок при условии, что каждая из них стягивается в точку. Этот предел не зависит ни от способа разбиения области а на части ни от выбора точек

В дальнейшем мы будем рассматривать только функции, непрерывные в области интегрирования.

Из теоремы существования следует, что мы можем, например, разбить область а на малые прямоугольники со сторонами прямыми, параллельными осям координат (рис. 230). При этом . Выбирая затем в каждом малом прямоугольнике по точке мы можем написать, согласно определению двойного интеграла

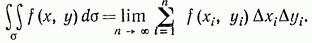
Для того чтобы подчеркнуть, что двойной интеграл можно получить как предел суммы вида вместо обозначения употребляют также обозначение

Итак,

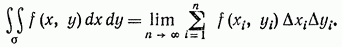
Выражение называется элементом площади в декартовых координатах и равно площади прямоугольника со сторонами параллельными координатным осям.

Заметим, что при составлении интегральной суммы площадки прилегающие к границе области а, не имеют формы прямоугольников. Однако можно доказать, что ошибка от замены таких площадок прямоугольниками с площадями в пределе сведется к нулю.

Свойства двойных интегралов

Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.

1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D₁ и D₂, то функция f(x, y) интегрируема в каждой из областей D₁ и D₂, причем

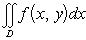
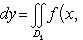
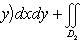
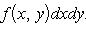
2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем

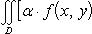
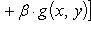
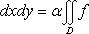
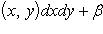
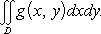
3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

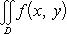
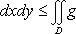
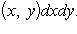
5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

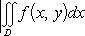
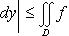
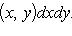
(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)

6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

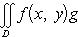
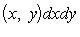
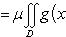
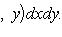(11)

В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид

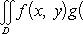
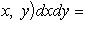
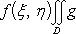
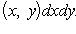
7°. Важное геометрическое свойство. 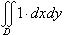равен площади области D (Это свойство, как уже отмечалось ранее, непосредственно вытекает из определения интегрируемости, данного в пункте Определение и существование двойного интеграла для произвольной области)