Вывод правила треугольников

1.

Матрица –это прямоугольная таблица чисел.

Равенство матриц

А=В, если 1. А_[mxn]=B_[mxn]

2. a_ij=b_ij

Соответствующие элементы – элементы с одинаковыми индексами

Две матрицы равны если они совпадают и их размерности равны

Операции над матрицами

I. Сложение

С_[mxn]= А_[mxn]+B_[mxn], если с_ij= a_ij+b_ij

Свойства сложения матриц

1. Коммутативность (переместительный закон)

А+В=В+А

Доказательствo:

Пусть С_[mxn]=А_[mxn]+B_[mxn], D_[mxn]=B_[mxn]+A_[mxn],

А) Размерности С и В совпадают

Б) с_ij= a_ij+b_ij, по определению

d_ij= b_ij+a_ij, но т.к. a_ij и b_ij – числа, то a_ij+b_ij= b_ij+a_ij→ c_ij=d_ij→C=В

1. Ассоциативность (Сочетательный закон)

(A+B)+C=A+(B+C)

Доказательствo:

D’=A+B, D=D’+C, P’=B+C, P=A+P’

А) Размерность D’_[mxn]=A_[mxn]+B_[mxm]

D_[mxn]=D’_[mxn]+C_[mxn], аналогично для P_[mxn]

Б)d’_ij= a_ij+b_ij; d_ij=d’_ij+c_ij= (a_ij+b_ij) +c_ij

p’_ij= b_ij+a_ij; p_ij=p’_ij+a_ij= a_ij+(b_ij +c_ij)

Для чисел aij, b_ij, c_ij справедливо равенство (a_ij+b_ij) +c_ij = a_ij+(b_ij +c_ij) →p_ij=d_ij→P=В

1. Нейтральный элемент относительно сложения

Θ такая, что Θ + А =А+ Θ=А

А) Размерности совпадают

Б) Θ_ij+a_ij=a_ij+Θ_ij→ Θ_ij=0

II. Вычитание

С=A-B, если А=В+С

c_ij=a_ij-b_ij

Противоположные матрицы – матрицы сумма которых равна 0.

Нулевая матрица – матрица все элементы которой равны 0

О=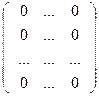

2.

II. Умножение матрицы на число

С=k*A, если

1) с_ij=ka_ij

2) размерности совпадают

Свойства операции

1. k(A+B)=kA+kB

2. (k+n)A=kA+nA

3. (kn)A=k(nA)=n(kA)

4. Вычитание можно представить как сложение с обратной матрицей

A-B=A+(-1)B

3.

IV. Транспонирование матриц

A= 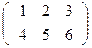A^т=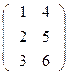

C_[mxn]=(A_[mxn])^т, если с_ij=a_ji

Свойства

1. (A+B)^т=А^т+В^т
2. (nA)^т=nA^т

Доказательствo: С=А^т, если c_ij=a_ji

B=nA, C=B^т (слева)

D=A^т, P=nD (справа)

А) Размерности B=nA

C=B^т, D=A^т, P=nD

б) Посвойству умножения элементы В совпадают с элементами А умноженными с тем же числом

b_ij=na_ij (слева)

d_ji=a_ij ,p_ji=nd_ji=na_ij

→p_ji=c_ji→B=C

1. (А^т)^т=А

4.

V. Произведение матриц

A_[mxn]*B_[nxr]=C_[mxr]

Согласованные матрицы-матрицы число столбцов 1 матрицы равно числу строк во 2

Если А и В согласованны то В и А не всегда

С называется произведением A*B, если

1. C_[mxn] =A_[mxr]*B_[rxn]

2. с_ij=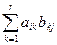

Элемент матрицы С, стоящий в i-й строке и j-м столбце равен сумме попарных произведений элементов i строки матрицы А на соответствующие элементы о столбца матрицы В.

Свойства

1. AB≠BA
2. (AB)C=A(BC) (без док)
3. A(B+C)=AB+AC
4. n(AB)=A(nB)
5. (AB)^т=В^тА^т

VI. Нейтральный элемент относительно умножения – единичная матрица (Е)

AE=A=EA

Единичная матрица – квадратная матрица все элементы которой, расположенные на гланой диагонали равны 1, а остальные 0.

E_ij=1, при i=j

VII. Умножение на нулевую матрицу

A_[mxn] Θ_[nxr]= Θ_[mxr]

5.

VIII. Возведение матрицы в степень

(A_[mxn])^k=AAAAAA…(k раз)

6.

Квадратная матрица – матрица у которой i=j.

Определитель матрицы – число.

Порядок определителя - количество строк или столбцов.

Теорема разложения.

Определитель матрицы А n-го порядка равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения.

7.

D₃=a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₂₁a₃₂a₁₃ – a₃₁a₂₂a₁₃ – a₃₂a₂₃a₁₁ – a₂₁a₁₂a₃₃

Вывод правила треугольников.

8.