Вычисления показывают, что для стандартных метрических резьб

σ_экв ≈ 1.3σ.

Это позволяет рассчитывать прочность болтов по упрощенной формуле

σ =1.3∙4F_зат/(πd₁²) ≤ [σ].

Отсюда внутренний диаметр резьбы

d₁ ≥ 1.3∙4F_зат/(π[σ]).

Расчетами и практикой установлено, что болты с резьбой меньше М10 - М12 можно разрушить при затяжке. Поэтому в сред­нем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8). В настоящее время некоторые заводы используют для затяжки болтов специальные ключи предельного момента. Эти ключи не позволяют приложить к гайке момент больше установленного. В таком случае отпадает необходимость ограничивать применение болтов малых диаметров.
3.1.6.3 Болтовое соединение нагружено силами, сдвигающими детали в стыке
Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах.
3.1.6.3.1 Болт поставлен сзазором
При установке болта сзазором (рисунок 3.10) внешнюю нагрузку F уравновешивают силами трения в стыке, кото­рые образуются от затяжки болта.
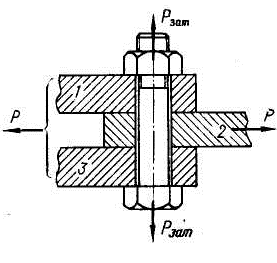Рисунок 3.10 Установка болта с зазором

Условие отсутствия сдвига деталей в стыке

KF ≤ iF_тр = iF_зат f, или F_зат =KF/(if),

где i - число стыков, стягиваемых винтом (по рисунку 3.10 число стыков i равно 2, при соединении только двух деталей 1 и 2, i = 1); f - коэффициент трения встыке (f ≈ 0,15…0,20 для сухих чугунных и стальных поверхностей); К - коэффициент запаса (К = 1,3…1,5 при статической нагрузке; К = 1,8… 2 при переменной нагрузке).

Внутренний диаметр резьбы винта

d₁ ≥ 1.3∙4KF_зат /(ifπ[σ]).
3.1.6.3.2 Болт поставлен без зазора
При установке болта без зазора (рисунок 3.11) отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим посадку типа напряженной. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта необязательна. В общем случае болт можно заменить штифтом. Стер­жень болта рассчиты­вают по напряжениям среза. Условие прочности по напряже­ниям среза

τ = 4F/(iπd²) ≤ [τ],

где i - число плоско­стей среза (на рис. 3.11 i = 2; при соединении только двух деталей i = 1).

Рисунок 3.11 Установка болта без зазора
Из условия прочности при срезе диаметр винта в опасном сечении

d ≥ 4F/(iπ[τ]).

3.1.6.4 Болт затянут, внешняя нагрузка раскрывает стык деталей
Примером могут служить болты для крепления крышек резервуа­ров, нагруженных давлением жидкости или газа (рисунок 3.12). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между эле­ментами такого соединения является статически неопределимой и решается с учетом деформации этих элементов. Обозначим: F_зат - сила затяжки болта; F = R/z - внешняя нагрузка соединения, приходящаяся на один болт (z - число болтов).

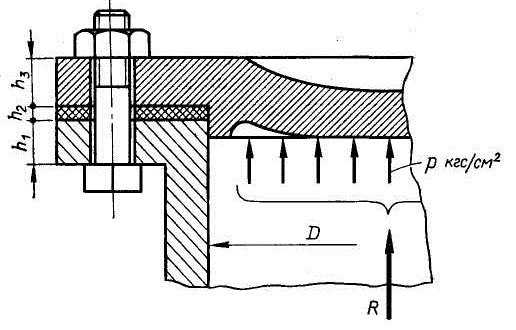
Рисунок 3.12 Крепление крышки резервуара

При затяжке соединения (рисунок 3.13, а) под действием силы F_зат стержень винта удлиняется на некоторую величину Δ_б, а соединяемые детали укорачиваются на величину Δ_д (рисунок 3.13, б).

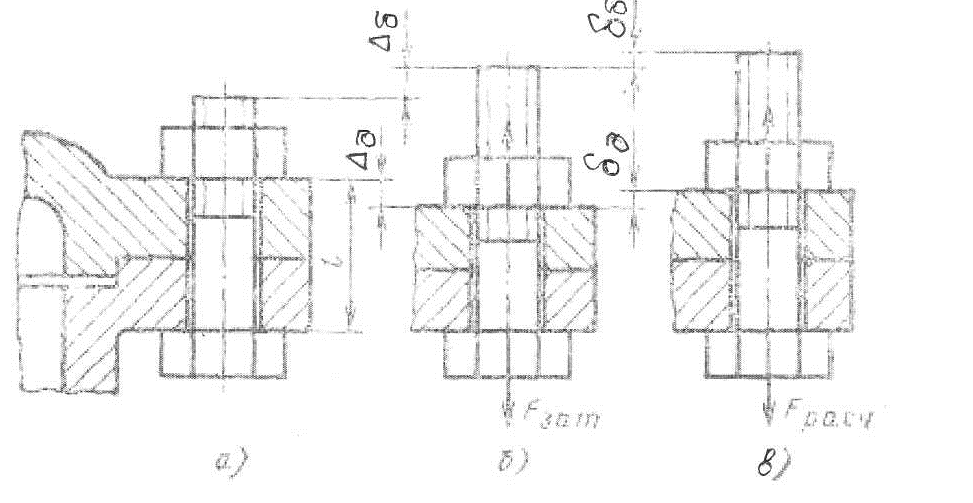
Рисунок 3.13 Деформация соединения при затяжке и приложении внешней нагрузки
После приложения внешней нагрузки Rк затянутому соединению винт дополнительно растянется на некото­рую величину δ_б, а деформация сжатия деталей уменьшится на такую же величину δ_д (рисунок 3.13, в). Это значит, что только часть внешней нагрузки дополни­тельно нагружает болт, а другая часть идет на разгрузку стыка.

Если обозначим χ - коэффициент внешней нагрузки (учитывает ту долю нагрузки F,которая приходится на болт), то дополнительная нагрузка болта будет равна χF,а уменьшение затяжки стыка - (1 - χ)F.Величина коэффициента χопределяется по условию равен­ства дополнительных деформаций болта и деталей (условие совмест­ности деформаций)

δ = χ F_б = (1- χ) F_д,

где _б - податливость болта; _д - суммарная податливость соединяемых деталей.

Из этого равенства

χ = _д/(_д + _б).

Далее получим:

- приращение нагрузки на болт

F_б = χF;

-расчетную (растягивающую) нагрузку болта

F_р = F_зат + χF;

- расчетную нагрузку с учетом крутящего момента при затяжке

F_р = 1.3F_зат + χF.

Остаточная затяжка стыка на один болт

F_ост = F_зат – (1 – χ)F.

Из этого уравнения может быть определена необходимая сила затяжки

F_зат = F_ост + (1 – χ)F.
^

Вопрос 35
ПЕРЕДАЧА ВИНТ—ГАЙКА
§ 14.1. Общие сведения
Передача винт — гайка служит для преобразования вращательного движения в поступательное. Основы теории винтовой пары (типы резьб, силовые и кинематические зависимости, к.п.д. и др.) изложены в гл. 1. Ниже излагаются только некоторые дополнительные сведения.
В винтовых механизмах вращение винта или гайки осуществляют обычно с помощью маховика, шестерни и т. п. При этом передаточное отношение условно можно выразить отношением окружного перемещения маховичка SM к перемещению гайки (винта) 5Г:
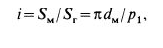где dM— диаметр маховичка (шестерни и т. п.); ργ—ход винта. При малом р{ и сравнительно большом dM можно получить очень большое /. Например, при ργ = 1 мм dM = 200 мм, / = 628.
Зависимость между окружной силой Ft на маховичке и осевой силой Fa на гайке (винте) запишем в виде

где η — КПД винтовой пары. Для / = 628 и η^0,3 получим Fa*\90Fr
Таким образом, при простой и компактной конструкции передача винт — гайка позволяет получать большой выигрыш в силе или осуществлять медленные и точные перемещения.
Основной недостаток передачи — низкий КПД. В соответствии с этим передачу винт — гайка применяют в механизмах, где необходимо создавать большие усилия (домкраты, прессы и т. п.), а также в механизмах точных перемещений (механизмы подачи станков, измерительные, установочные и регулировочные механизмы).
Разработано много конструкций специальных винтовых пар, которые позволяют компенсировать ошибки изготовления, зазоров и износа; обеспечивают очень большие передаточные отношения (дифференциальная двойная резьба с разным шагом); повышают КПД путем замены трения скольжения трением качения (шариковые винтовые пары) и т. п. (см. [15]).
§ 14.2. Особенности расчета резьбы винтовых механизмов
Основным критерием работоспособности этих резьб является износостойкость. В целях уменьшения износа применяют антифрикционные пары материалов (сталь — чугун, сталь —
бронза и др.), смазку трущихся поверхностей, малые допускаемые напряжения смятия [асм]. Значение асм в ходовой резьбе выражается такой же формулой, как и в крепежной [см. формулу (1.13)], а именно:

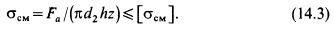
Для проектного расчета формулу (14.3) целесообразно преобразовать, заменив z = H/p и обозначив:

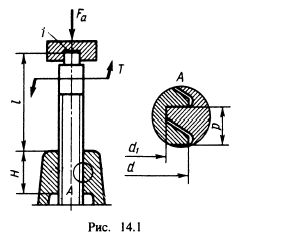
винт домкрата

При этом получим (14.5) Здесь ψΛ = 0,5 — трапецеидальная и прямоугольная резьбы (см. рис. 1.5,6, а); ψΛ=0,75 — упорная резьба (см. рис. 1.5, в). Значение коэффициента высоты гайки выбирают в пределах ψΗ= 1,2...2,5. Значение [асм] в резьбе для пар; закаленная сталь — бронза [асм ]= 11... 13 Μ Па; незакаленная сталь — бронза [tfCM] = 8...10 МПа; незакаленная сталь — чугун [асм] = 4...6 МПа. Значение [асм] в резьбе винтовых механизмов точных перемещений, например в делительных цепях станков, принимают в 2...3 раза меньше, чем винтов общего назначения. После расчета по формуле (14.5) значение d2 согласуют со стандартом. В ходовых винтовых парах неравномерность распределения нагрузки по виткам выравнивается вследствие приработки резьбы. Поэтому здесь допускают более высокие гайки, чем в крепежных изделиях. После расчета резьбы винты, работающие на сжатие, например винты домкратов, проверяют на прочность и устойчивость. Методика такого расчета изложена в примере. Пример расчета 14.1. Рассчитать винт домкрата, нагруженный по схеме рис. 14.1, а также определить его КПД. Резьба самотормозящая, упорная. Грузоподъемность Fe = 150000 H, /=1000 мм, вийт—сталь 35, гайка — чугув, подпятник 1 шариковый. Решение. 1. Определяем диаметр винта по условию износостойкости—формула (14.5), приняв [асм] = 6 МПа, ^, = 2,1; ψΑ=0,75: d2 50000/(π • 2,1 • 0,75 ■ 6) =71,1 мм. По таблицам стандарта выбираем резьбу 85x12 (рис. 14.1): </=85 мм; /?=12 мм; <^=64,2 мм; </2 = 76мм; А = 9 мм.     Стандартом предусмотрены три шага (/?=20; 12; 5 мм) для данного диаметра резьбы. Выбор шага резьбы в данном случае зависит от соблюдения условия само^рможения ψ<φ. Принимая для смазанного винта /=0,1, получим 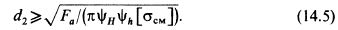    что обеспечивает достаточный запас самоторможения. При шаге р — 20 мм, ψ = 5° 10' запас самоторможения был бы недостаточным. Из формулы (14.4) имеем высоту гайки #=ΨΗ • d2 = 2,1 • 76 = 159,6 мм. Назначаем #= 160 мм. Так как стержень винта работает на сжатие и имеет большую свободную длину, его необходимо проверить на прочность с учетом устойчивости по формуле σ = 4/Γα/(π^?)^γ[σ]. Для материала винта (см. табл. 1.1), принимая коэффициент запаса прочности 5 = 2, получаем [σ] = στ/$ = 320/2= 160 МПа. Коэффициент уменьшения допускаемых напряжений γ для сжатых стержней выбирают в зависимости от гибкости λ:

Вопрос 36

Внутренний диаметр винта ориентировочно определяют из расчета на сжатие по пониженному (примерно на 30%) допускаемому напряжению:

где Q - нагрузка, Н; d₁ - внутренний диаметр винта, мм.

Должно быть самоторможение винта, т. е. - угол подъема винтовой линии β дол­жен быть меньше угла трения р:

tgβ= P/(πd₂)

где р - шаг резьбы винта; d₂ - средний диаметр резьбы винта.

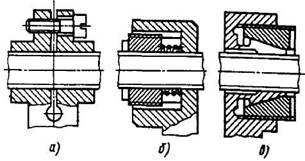
Рис. 3. Способы устранения зазоров:

а - за счет стягивания винтом; б - пружиной; в - цанговым зажимом

Если принять коэффициент трения в резьбе f = 0,1, то tgp = 0,1, или р = 5°43'.

Винт проверяют на совместное действие сжатия и кручения, а при значительной длине - и на устойчивость (продольный изгиб). Крутящий момент

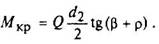
Приведенное напряжение

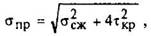
где τ_кр = M_кр / 0,2d₁³ - касательное напряжение, МПа.

Условие достаточной прочности

σ_пр = [σ_p].

Допускаемое напряжение на растяжение [σ_р] =70…90МПа.

На устойчивость винт проверяют по формуле Эйлера

где P_кр - критическая сила, Н;

Е - модуль упругости, МПа;

J_расч- момент инерции поперечного сечения винта, мм⁴;

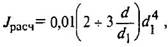
где d - наружный диаметр винта; d₁ -внутренний диаметр винта; l - длина вин­та, мм (расстояние от середины гайки до опорной поверхности головки винта при вывернутом до отказа винте, причем винт рассматривается как стержень с шарнирно закрепленными концами).

Запас устойчивости

n_у = P_кр / Q,

рекомендуется n_у ≥ 4.

Допускаемые давления

Материал	[q], МПа
Сталь по чугуну	5-6
Сталь по антифрикционномучугуну	10-13
Сталь по стали	7-13
Сталь по бронзе	7-13

Формула Эйлера применима при усло­вии, что гибкость стержня λ = l/i больше предельной (λ > λ_пред), где i– радиус инерции поперечного стержня (для круглого сечения i = d/4).

Для стали λ_пред ≈ 100. При гибкости меньше предельной определяют критиче­ское напряжение в МПа:

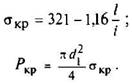
При гибкости λ < 60 расчет на устойчи­вость является излишним.

Высоту гайки определяют из расчета на допускаемое давление [q] (табл. 8) между витками винта и гайки:

H = zP,

где Р - шаг резьбы; z - полезное число витков, zдолжно быть не более 10, так как остальные витки не будут работать.

Если z > 10, то переходят либо на дру­гие материалы, либо увеличивают d и d₁:

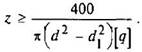
Усилие рабочегоРр, необходи­мое для подъема груза Q . Из уравнения

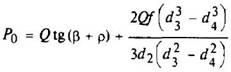
определяют P₀ - усилие, необходимое для вращения винта, приложенное по среднему диаметру резьбы. Первый член правой час­ти уравнения представляет собой часть этого усилия, необходимую для подъема груза и преодоления трения в резьбе.а второй член - часть усилия, необходимую для преодоления силы трения на кольцевой поверхности стыка между вращающимся винтом и неподвижной чашкой. При длине рукоятки L усилие Р_р находят из условия равенства моментов сил P₀ и Р_р относи­тельно оси винта:

Р₀·d²/2 =P_pL.

КПД домкрата

η = A_п/А_з

где А_п = QP - полезная работа подъема груза за один оборот винта;

А_з = P₀πd₂ - затраченная работа за один оборот винта.

Резьбу грузовых винтов делают прямо­угольной и трапецеидальной.

Пример расчета домкрата. Произвести проверочный расчет домкрата с Q = 60000Н с данными, приведенными на рис. 4.

Винт изготовлен из стали 35, гайка - из бронзы, резьба однозаходная с шагом 10мм.

1. Определим КПД домкрата:

а) угол β подъема винтовой линии прямоугольной резьбы (при среднем диа­метре d₂)

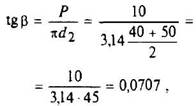
или β = 4°03';

б) угол трения р при f = 0,12, tgp = 0,12, или р = 6º51';

в) условие самоторможения будет при β ≤ p,

г) условие преобразования поступатель­ного движения во вращательные будет при р ≥ 2р;

д) работа за один оборот винта, необхо­димая для подъема груза и преодоления силы трения в резьбе,

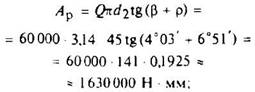
е) работа за один оборот винта, необхо­димая для преодоления трения на торцовой части винта при f₁ = 0,14:

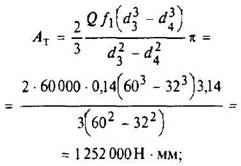
ж) полезная работа подъема груза

А_п = QP = 60000·10 = 600000Н · мм;

з)КПД

2. Определяем усилие рабочего Р_р при подъеме груза. При длине рукоятки 1000м работа за один оборот

А_з = Р_р · 2πL = P_p· 6,28 · 1000 = 6280Р_р;

эта работа должна быть равна А_р +А_т, т.е. 6280Р_р = 2882000Н·мм, откуда

Р_р = 2882000/6280 = 458Н.

Усилие Р_р очень велико, поэтому при­дется приложить усилие двух рабочих, так как на одного рабочего принимают Р_р = 150…300Н.

3. Проверяем напряжение в винте:

а) расчетная длина винта

l = 390+70-100/2 = 410мм;

б) радиус инерции круга диаметром d₁ = 40мм

i= d₁/4 = 40/4 = 10мм;

λ = l/i= 410/10 = 41,

при такой малой гибкости проверки на устойчивость не требуется;

в) нормальное напряжение

σ_сж = Q/F = 60000/(3.14·40²/4) = 47,8МПа;

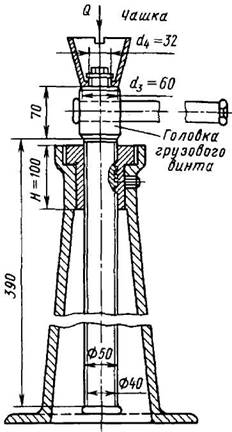
Рис. 4. Схема к расчету домкрата

г) касательное напряжение

где крутящий момент

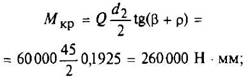
д) приведенное напряжение

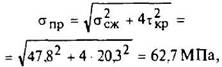
для винта из стали 35 при статической на­грузке допустимо σ_в = 85,0МПа.

4. Проверяем высоту гайки:

а) число витков в гайке

z = H/P = 100/10 = 10;

б) удельное давление

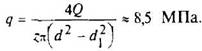
Результат расчета удовлетворительный, так как величина находится в пределах, указанных в табл. 8.