Главная часть бесконечно-малой.

Определение. Если 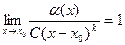то функция 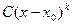называется ГЛАВНОЙ ЧАСТЬЮ бесконечно-малой .

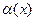Фактически, это степенная функция, эквивалентная данной 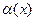. Если найти коэффициент 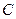и степень 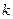, то мы найдём такую степенную функцию, график которой наилучшим образом (среди всех степенных) похож на график функции 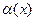в окрестности точки.

Пример. Найти главную часть бесконечно-малой в точке 0.

Решение. Так как точка 0, то 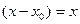, то есть главная часть имеет вид 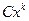. Запишем отношение данной бесконечно-малой и «эталонной» степенной. Нужно потребовать, чтобы этот предел был 1, ведь мы ищем именно эквивалентную бесконечно-малую.

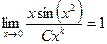. Преобразуем выражение с целью его упростить. Домножим и поделим на 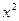, этим мы фактически можем заменить 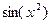на 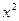. Параметры C и k пока просто переписываем, не меняя их в процессе преобразований.

= .

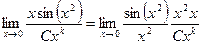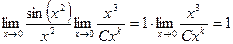Полное сокращение всех 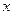будет лишь в случае k=3, а иначе предел 0 или 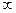, и не будет равен 1.

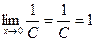, тогда С = 1. Итак, = .

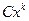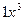Ответ. .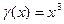

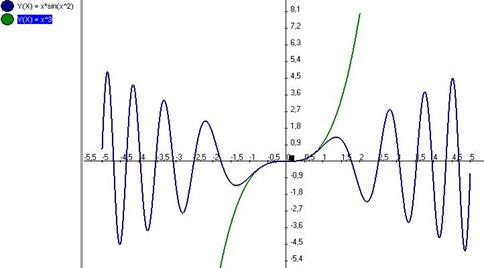
Ниже изображены графики бесконечно-малой и её главной части:

как видно, вблизи (0,0) они практически неотличимы.

Задачи на поиск главной части по методам и сложности похожи на вычисление lim, но фактически это обратная задача: при вычислении предела внутри нет параметров, а предел неизвестен, здесь же наоборот, известно, что предел равен 1, но внутри выражения неизвестные параметры C, k, которые надо найти, так, чтобы предел был равен 1.

Если учесть не только одну степенную функцию, но добавить ещё и последующие степени, то можно построить ещё более точное приближение. Это будет изучено позже, тема «формула Тейлора».

Непрерывность и точки разыва.

Односторонние пределы.

Бывают такие ситуации, когда функция определена только пр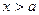и или 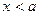. В этом случае тоже можно вычислять предел, но область определения пересекается только с правой или левой полуокрестностью.

Определение. Число 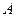называется правосторонним пределом функции 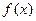в точке 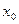, если: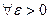 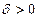, так, что при 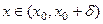выполняется: .

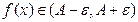Обозначается .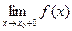

Аналогично,

Определение. Число 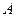называется левосторонним пределом функции 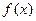в точке 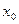, если: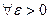 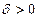, так, что при 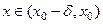выполняется: .

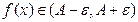Обозначается .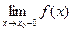

Односторонние пределы очень полезны при изучении функций, так как существуют такие ситуации, когда график функции слева и справа от некоторого 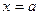стремится к разным ординатам.

Если односторонние пределы равны между собой, то существует предел функции в точке, если они разные, то предел не существует: ведь тогда 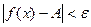для одной полуокрестности, но для второй полуокрестности эта разность не может быть меньше чем 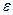, она будет .

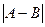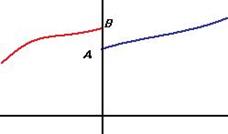
Представьте себе физический пример: температура 0 градусов. Если она понижается, проходя через 0, то есть до этого была положительна, то вода ещё не замёрзла, снега на улице нет. Если же она повышается и проходит через 0, например в марте, ситуация совсем иная - снег ещё не успел растяать. Как видно, ситуация при 0 градусов сильно зависит от того, какая температура была до этого.

Определение. Функция называется непрерывной в точке 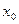, если в этой точке определено значение 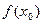, и оно совпадает как с правосторонним так и с левосторонним пределами:

.

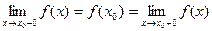Классификация:устранимый разрыв, разрыв 1 и 2 рода.

Устранимый разрыв.

Точка разрыва называется устранимой, если односторонние пределы равны 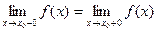причём равны конечному числу, но не существует 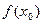или оно не равно пределу.

Пример. 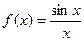. Формально 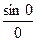вычислить нельзя, но предел есть, он раен 1. Получается график с одной выколотой точкой.

Пример. 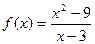. Точка 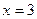- точка устранимого разыва. Значение не существует, но предел есть.

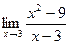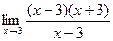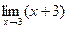= = = 6.

Можно доопределить значение функции в одной точке, то есть устранить разрыв. Поэтому он и называется устранимым.

Неустранимые разрывы делятся на 2 типа: