Методические рекомендации по изучению дисциплины и организации самостоятельной работы студентов

На теоретическую часть дисциплины отведено всего 4 часа.

На выполнение домашних заданий запланировано по 4 часа на каждое задание. В библиотеке Томского филиала академии правосудия для эффективной самостоятельной работы студентов имеется электронный обучающий видеокурс «Математика для юристов».

Основные рекомендации по организации самостоятельной работы студента сводятся к следующему:

1. Работа студента над учебным материалом начинается с теории. Рекомендуется вести подробный конспект.

2. При подготовке к самостоятельному выполнению заданий необходимо проработать теоретический материал по соответствующей теме, дополненный соответствующими выдержками из учебников и учебных пособий, имеющихся в библиотеке филиала.

3. Выполнение каждого задания рекомендуется начинать с решения простой задачи по теме. Потом прорабатываются теоретические вопросы и решаются более сложные задачи.

4. Для получения зачета необходимо выполнить индивидуальное контрольное задание, которое будет выдано преподавателем на установочном занятии, и ответов на контрольные вопросы.

5. Отчетность за семестр – зачет.

Методические указания для решения варианта самостоятельной работы студентов.

Тема 1. Под множеством понимают объединение в единое целое определенных вполне различимых предметов (объектов), которые при этом называются элементами образуемого ими множества, т.е. множество – это совокупность объектов произвольной природы, объединенных каким-то общим для них признаком.

Если а – элемент множества М, то это обозначают: аÎМ (а принадлежит М). Пример: множество статей Уголовного кодекса РФ.

Задача 1. Для заданных дискретных множеств А и В найти АUВ, А∩В, А\В, если А={2, 4, 6}, В={-2, 2, 8,10}, универсальное множество Ω={-4, -2, 2, 4, 6, 8, 10, 12}.

Решение. АUВ – это объединение множеств (или сумма), т. е. все элементы обоих множеств. Таким образом, АUВ= {-2, 2, 4, 6, 8, 10} (повторяющиеся элементы берутся один раз).

А∩В –это пересечение множеств, т.е. их общая часть. В нашем задании А∩В= {2} (множество, состоящее из одного элемента).

А\В – это разность множеств, т.е. элементы множества А, после удаления из него элементов, принадлежащих также множеству В. В нашем задании А\В = {4. 6}.

Задача 2. Для заданных непрерывных множеств А и В найти АUВ, А∩В, А\В, если А=[-4, 4], В=(-∞, 0), универсальное множество Ω=(-∞, ∞).

Решение. Эти задачи удобно решать, используя графическое представление. Нарисуем числовую ось и отметим на ней заданные интервалы.

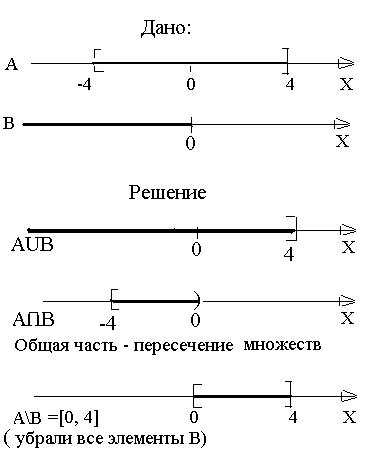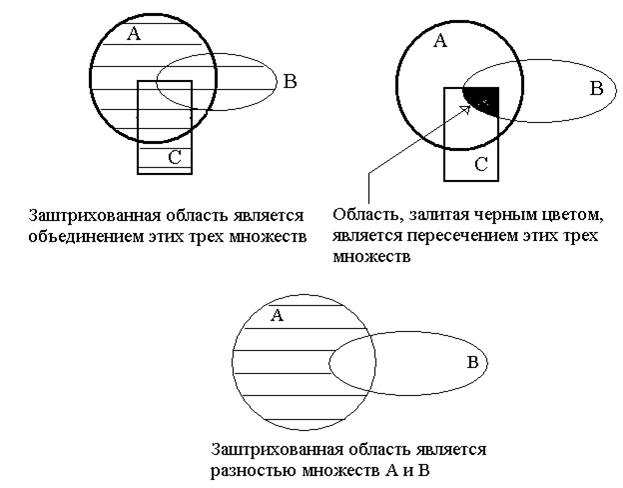
Задача 3. Решать задачи с непрерывными множествами можно с помощью другого графического метода, в котором множества изображаются любыми плоскими геометрическими фигурами: кругами, прямоугольниками, эллипсами и т.д. Это метод диаграмм Венна-Эйлера.

Даны множества А, В, С.

Найти:

a) их объединение АUВUС;

b) их пересечение А∩В∩С;

c) разность А и В (С отсутствует).

Решение.

Тема 2.Решение 3-х типов задач на проценты. Процентом называется сотая часть какого-либо числа (обозначается %). Если данное число принять за единицу, то 1 % составляет 0,01= 1/100.

Задача 1. В поселке N было совершено 52 правонарушения за год. Известно, что 5 % из них было совершено в январе месяце. Сколько правонарушений было совершено в январе.

Решение. Эта задача решается с использованием пропорции и ее основного свойства: произведение крайних членов пропорции равно произведению средних членов.

Составим пропорцию: 52 – это 100 %

Х – это 5 %.

Применяем основное свойство пропорции: 52 ·5=Х·100. Выразим отсюда Х: Х= 52·5/100. Ответ: 2,6 правонарушений.

Задача 2. Для обеспечения охраны общественного порядка выделяется 12 сотрудников УВД, что составляет 10 % от количества людей, участвующих в митинге. При каком количестве людей на митинге можно обеспечить порядок 300 сотрудниками УВД?

Решение задачи осуществляется в 2 этапа. На первом этапе определим, при каком количестве людей может быть обеспечена охрана общественного порядка 12 сотрудниками УВД. Составляем пропорцию:

12 чел. – 10 %

Х чел. – 100 %

Отсюда Х= 12·100/10= 120 человек митингующих.

На втором этапе определим, при каком количестве митингующих может быть обеспечена охрана общественного порядка 300 сотрудниками УВД.

Составим пропорцию:

120 митингующих – 10 сотрудников

Х митингующих – 300 сотрудников.

Отсюда получаем: 120·300=Х·10, т. е. Х= 120·300/10=3600.

Ответ: 3600 митингующих.

Задача 3. В США в 1980 году было совершено 23040 убийств, а в 2000 году – 15517. Сколько процентов составляет число убийств в 2000 году по сравнению с 1980 годом?

Решение: составим пропорцию:

23040 убийств – это 100 %

15517 убийств – Х %

Используем основное правило пропорции, тогда 23400·Х=15570·100. Выразим Х: Х= (15517·100)/23040=67,35 %.

Ответ: 67,35 %.

Тема 3.Решение задач на определение числа всевозможных видов объединения объектов: перестановок, сочетаний и размещений. Для успешного решения этих задач важно правильно определить вид соединения объектов в группы и применить соответствующую этому виду формулу.

Перестановками из n элементов называются соединения (объединения, выборки, комбинации) из элементов, отличающихся только порядком их расположения. Перестановки вычисляются по формулеp_n= n!=1·2·3···( n-1)· n, (здесь !–означает факториал, например, 5!=1·2·3·4·5=120).

Сочетаниями называются все возможные комбинации по m элементов из n элементов, которые отличаются друг от друга по крайней мере хотя бы одним элементом. Сочетания вычисляются по формуле:

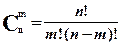Размещениями из n элементов по m называются такие соединения, которые имея по m элементов, отличаются как составом, так и порядком их размещения. Их число находится по формуле

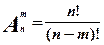Задача 1. Порядок выступления 8 участников соревнования по стрельбе определяется жребием. Сколько различных исходов жеребьевки при этом возможно?

Решение. Число участников n=8. Один вариант жеребьевки отличается от другого только порядком расположения участников. Поэтому для решения можно использовать формулу для подсчета числа всевозможных перестановок 8 участников соревнований. Вычислим число всевозможных перестановок из 8 участников соревнования.

P₈= 8!= 1·2·3·4·5·6·7·8=40320.

Задача 2. Сколькими способами можно составить дозор из 3 солдат и 1 офицера, если имеется 80 солдат и 3 офицера.

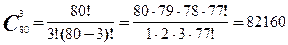Решение. Из 80 солдат нужно составить группы по 3 человека. Одна группа отличается от другой, если в ней есть хотя бы один другой солдат, при этом порядок солдат в группе не важен. Поэтому для решения задачи подходит формула подсчета числа всевозможных комбинаций по 3 человека из 80 солдат. Вычислим число сочетаний из 80 по 3 элемента:

Так как с каждой командой из солдат может пойти любой офицер, то всего способов составления дозоров будет 82160·3= 246480.

Задача 3. На 7 сотрудников районного суда выделены 5 путевок. Все путевки различны. Сколькими способами можно их распределить?

Решение. В списках получивших путевку всегда будет фамилии 5 сотрудников из 7. Два списка, содержащие одни и те же фамилии, но расположенные в разном порядке, нам надо считать различными, так как для сотрудников не безразлично, напротив какой путевки поставлена его фамилия, т.е. важен не только состав списка, но и порядок расположения фамилий в нем, поэтому для решения задачи надо использовать формулу числа размещений из 7 по 5:

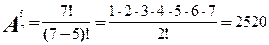Тема 4.Для успешного решения задач по теории вероятности студентам надо знать определения случайного события, видов случайных событий (достоверное, невозможное, случайное), классическое и статистическое определение вероятностей, основные теоремы вероятностей, понятие случайной величины и законов ее распределения.

Задача 1. В учебную группу выделили 9 книг, из которых 6 справочники. Найти вероятность того, что среди 5 взятых наугад книг равно 3 окажутся справочниками.

Для решения этой задачи надо вспомнить определение классической вероятности: «Вероятностью Р(А) события А называется отношение числа m равновозможных частных случаев, благоприятствующих событию А, к общему числу n всех таких случаев, т.е. Р(А)= m/n».

Назовем событием А событие, когда среди 5 взятых наугад книг окажется 3 справочника.

Сначала рассчитаем число благоприятных событий. Число комбинаций из 6 справочников по 3 можно рассчитать по формуле сочетаний:

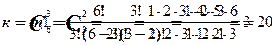Из 3 не справочников можно составить n1 вариантов по 2 книги:

Таким образом, число благоприятных случаев, когда 3 книги справочники, а 2 –обычные, будет равно к·n1= 20·3=60.

Теперь рассчитаем общее число всех возможных случаев выбора 5 книг из 9:

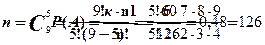Применим формулу классической вероятности и получим:

Ответ: Вероятность того, что среди 5 взятых наугад книг равно 3 окажутся справочниками равна 0,48.

Задача 2. Среди 100 книг есть 1 книга известного юриста. Выбрали наугад 10 книг. Какова вероятность того, что среди них есть книга известного юриста?

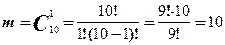Решение. Назовем благоприятным событием А случай, когда в числе выбранных наугад 10 книг имеется книга известного юриста. Подсчитаем число благоприятных событий:

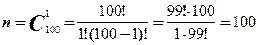Подсчитаем число всех возможных вариантов выбора:

По формуле классической теории вероятностей вычислим P(A):

P(A)=m/n=10/100=0,1

Задача 3. На баллистическую экспертизу в одной коробке поступили 7 гильз от автомата Калашникова отечественного производства, 5 гильз такого же автомата, но китайского производства и 3 гильзы от автомата польского производства. Найти вероятность того, что первая наугад вынутая гильза окажется от автомата отечественного производства (событие А1), вторая гильза – китайского производства (событие А2) и третья гильза – польского производства (событие А3).

Решение. Всего поступило гильз n=7+5+3=15. Общее число исходов (возможных вариантов) при выборе 1 гильзы из 15 равно 15. Благоприятный случай, если будет выбрана гильза отечественного производства. Так как их 7, то благоприятствующих событию А1 случаев возможно ровно 7. Вычислим вероятность события А1 по формуле классической вероятности P(A1)=7/15.

Событие А2 зависит от условия, что первой выбранной гильзой была отечественная (т.е. от события А1), поэтому ее рассчитываем по формуле условной вероятности: P(А2/_A1)=5/(15-1)=5/14.

Событие А3 зависит от условия, что первой выбранной гильзой была отечественная, а второй – китайского производства (т.е. зависит от событий А1 и А2). Поэтому рассчитываем вероятность наступления события А3 по формуле условной вероятности: P(А2/_A1·А2)=3/(15-2)=3/13.

Теперь вероятность наступления событий А1, А2, А3 в указанном порядке можно рассчитать по формуле полной вероятности:

Р(А1, А2, А3)=Р(А1)·P(А2/_А1)·Р(А3/ _A1·А2)=7/15 · 5/14 · 3/13=1/26≈0,038.

Тема 5.Для обобщения и анализа статистических данных очень важно уметь определять основные характеристики выборочных данных, такие как среднее арифметическое значение, среднее взвешенное, структурные средние (мода и медиана), а также оценивать вариацию данных (среднее квадратическое отклонение, коэффициент вариации и др.).

Среднее арифметическое значение (простое) n данных равно сумме данных, разделенной на их количество. Используется, когда данные не повторяются.

Средним арифметическим взвешенным называется такое среднее, при расчете которого значение усредняемого признака взвешивается по значениям других признаков. Используется, когда данные повторяются.

Медиана – это величина, находящаяся посередине набора данных, когда в нем все значения упорядочены по возрастанию или убыванию.

Мода – это наиболее часто встречающееся значение.

Задача 1. В стадии расследования у старшего следователя находятся пять уголовных дел с числом обвиняемых 1, 3, 2, 5 и 4. Определите среднее число обвиняемых на одно уголовное дело.

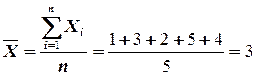Решение. Каждая единица совокупности (число обвиняемых в уголовных делах) имеет различные значения изучаемого признака X_i (от 1 до 5), т.е. его значения не повторяются. Значит, для определения среднего числа обвиняемых на 1 уголовное дело применим формулу средней арифметической простой:

Задача 2. В следственном отделе районного УВД находятся дела о хищении имущества, характеризующиеся следующими данными:

Число обвиняемых	Число дел

Определите среднее число обвиняемых на одно уголовное дело.

Решение. Значения изучаемого признака повторяются, поэтому для определения среднего числа обвиняемых на одно уголовное дело применим формулу арифметической средней взвешенной:

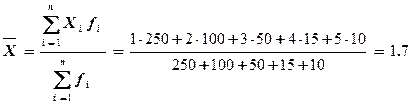В этой формуле X_i – это признак, а f_i – число повторений признака.

Задача 3. Предположим, в районном суде оформлением передачей дел в архив занимаются 2 сотрудника. Первый из них на одно дело затрачивает 1 час, второй – 1,5 часа. Каковы средние затраты времени на одно дело, если общая продолжительность рабочего времени у сотрудников равна?

Решение. На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на одно дело, т.е. (1+1,5):2=1,25 часа.

Проверим обоснованность такого подхода на примере одного дня работы. За день первый сотрудник обработает 8:1=8 дел, второй 8:1,5=5,3 дела, что в сумме составит 13,3 дела. Если заменить индивидуальные значения их предполагаемым средним значением, то общее число переданных в архив дел обоими сотрудниками будет 8/1,25 + 8/1,25≈12,8 дела, т.е. уменьшится.

Если подойдем к решению задачи через исходное соотношение средней, то получим, что для определения средних затрат времени необходимо общие затраты времени за любой интервал разделить на общее число оформленных за этот интервал двумя сотрудниками дел:

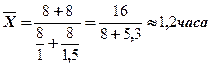Если теперь заменим индивидуальные значения их средней величиной, то общее число оформленных и переданных в архив дел за день не изменится:

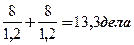
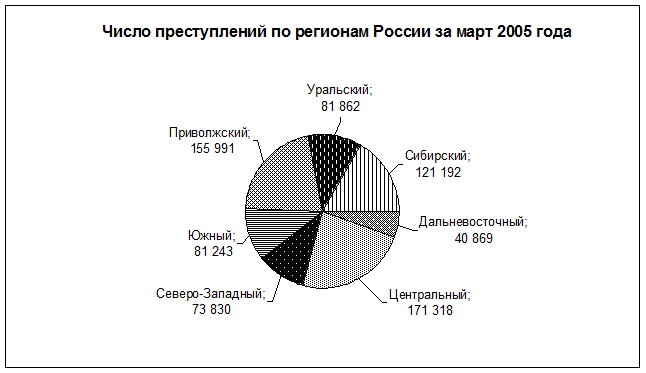
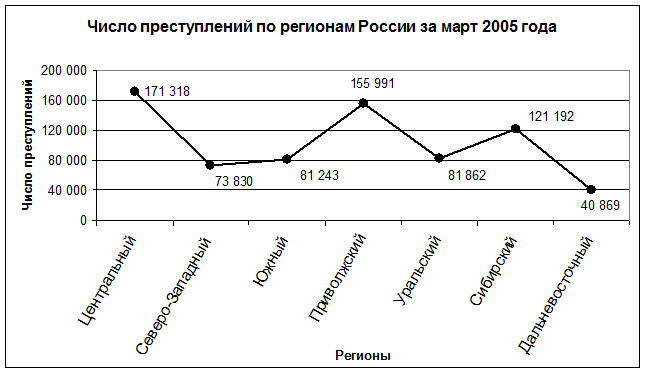
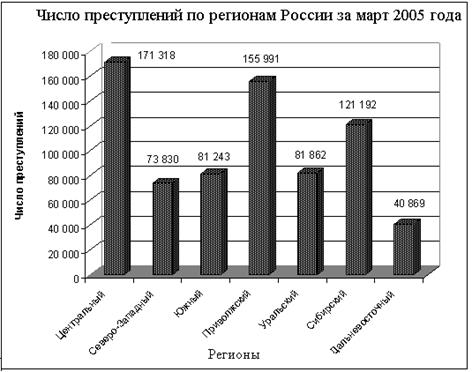
Задача 4. Имеются табличные данные по состоянию преступности в регионах России на март 2005 года. Изобразите данные графически несколькими способами.

Регионы России (федеральные округа)	Зарегистрировано преступлений
Центральный	171 318
Северо-Западный	73 830
Южный	81 243
Приволжский	155 991
Уральский	81 862
Сибирский	121 192
Дальневосточный	40 869

Эти данные можно наглядно представить в виде линейного графика, столбчатой и секторной диаграмм, которые легко построить в электронной таблице Excel.

Решение.