Дифференциальные уравнения. Переменная называется бесконечно малой, если в процессе своего изменения она становится и остаётся по модулю меньше любого на период заданного числа :

Пределы

Переменная 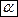называется бесконечно малой, если в процессе своего изменения она становится и остаётся по модулю меньше любого на период заданного числа :

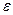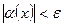— бесконечно малая величина (БМВ)

Переменная 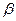называется бесконечно большой, если в процессе своего изменения она становится и остаётся по модулю больше любого на период заданного числа :

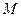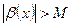— бесконечно большая величина (ББВ)

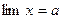
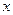Число будет пределом переменной , если разница между переменной и пределом будет бесконечно малой.

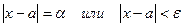
Надо помнить, что:

– предел БМВ равен нулю: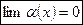

– предел ББВ равен бесконечности: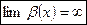

Свойства пределов:

1. Предел постоянной равен самой постоянной:

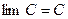
2. Предел суммы равен сумме пределов (если такие пределы существуют):

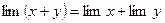
3. Предел произведения равен произведению пределов (если такие пределы существуют):

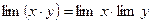
4. Предел частного равен частному пределов (если такие пределы существуют, и знаменатель отличен от нуля):

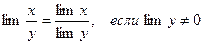
5. Предел от функции равен функции от предела:

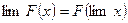
6. Предел степени равен пределу основания, возведённому в предел показателя степени:

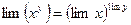
За величину, стремящуюся к бесконечности, часто обозначают 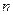(но не обязательно).

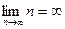
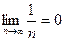
Порядок вычисления пределов:

1) Подставить число, к которому стремится переменная, вместо x. Если возможно провести вычисление, тем самым найти ответ:

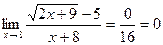
2) Чаще всего при подстановке возникают неопределённости:

· Неопределённость вида :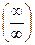

Для решения предела необходимо и числитель и знаменатель разделить на x в наивысшей степени, например:

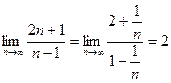
Можно увидеть, что при решении всех пределов с неопределённостью вида 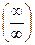ответ будет равен отношению коэффициентов при переменных в наивысших степенях, т. е.

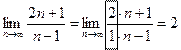
· Неопределённость вида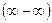

Для решения предела необходимо привести его к виду 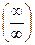путём домножения предела на дробь, где и числитель и знаменатель — сопряжённые множители для предела. Например:

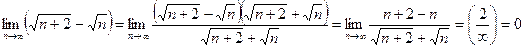
· Неопределённость вида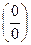

Решается путём сокращения числителя и знаменателя на БМВ.

Находится БМВ исходя из её определения — это есть величина, которая стремится к нулю:

Например, если 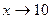, то 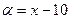(т. е. БМВ является разность 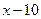) и. т.п.

Для сокращения в дроби БМВ можно разложить числитель или знаменатель по формулам сокращённого умножения (см. Таблицы).

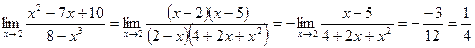
Также для деления числителя и знаменателя на БМВ используется деление многочленов столбиком.

Если в пределе имеются тригонометрические функции (sin, cos, arctg и т. д.), а также при подстановке переменной получается неопределенность 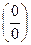, то велика вероятность того, что надо воспользоваться заменой, тригонометрическими формулами, а также первым замечательным пределом:

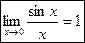— первый замечательный предел

В соответствии с ним в пределах можно делать замену (только при умножении синусов, косинусов и т. п.):

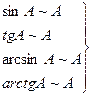всё это можно делать, только если ,

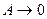где A — выражение, содержащее переменную.

Например:

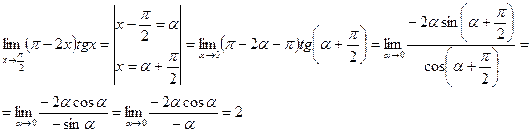
· Неопределённость вида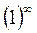

Такие пределы решаются с помощью второго замечательного предела:

Второй замечательный предел

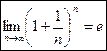
или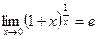

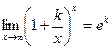
Рассмотрим пример:

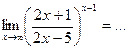в скобках выделяем единицу и БМВ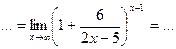

Далее домножаем числитель и знаменатель показателя степени на величину, обратную БМВ в скобочках:

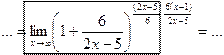
Всё, что обведено в рамку = e (исходя из второго замечательного предела), тогда:

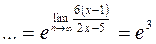
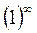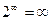!!! Учтите, что неопределённостью является только ! Так , а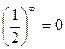

Производные

Дифференциальные уравнения

Дифференциальные уравнения имеют вид:

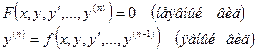
Порядок дифференциального уравнения зависит от наивысшего порядка производной, входящей в это уравнение:

Дифференциальные уравнения любого прядка можно решать последовательным интегрированием только если слева от знака “=” стоит производная любого порядка, а справа от знака “=” стоит функция только от x:

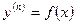
Например:

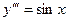
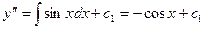
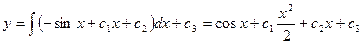
Общим решением дифференциальных уравнений является:

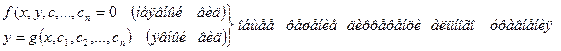
В общем решении должны присутствовать произвольные постоянные. Их столько, каков порядок дифференциального уравнения.

Частное решение получается из общего при определённых значениях произвольных постоянных. Чтобы найти частное решение, обязательно должны быть начальные условия.

Геометрически общее решение дифференциального уравнения — семейство интегральных кривых. Чтобы найти частное решение, надо найти определённые произвольные постоянные. Частное решение — единственная интегральная кривая, проходящая через точку, соответствующей начальным условиям.