Остроение окончательной эпюры изгибающих моментов.

После вычисления единичных коэффициентов и грузовых членов канонических уравнений эти уравнения решают. В результате чего определяют неизвестные усилия. После того, как лишние неизвестные найдены, эквивалентное состояние будет представлять собой статически определимую систему, находящуюся под действием заданной нагрузки и найденных сил Х_i . Рассчитав эту статически определимую раму, строят для нее эпюры усилий M, N, Q , известными способами, которыми пользовались при построении эпюр для статически определимых рам.

Существует и другой способ построения эпюры М. На основании принципа Даламбера, эпюру М можно построить на основании формулы:

М_ок = М₁·Х₁ + М₂·Х₂ + … + М_n·Х _n + М_Р = М_i·Х _i + М_Р

Т.е. для получения окончательной эпюры изгибающих моментов ординаты каждой их единичных эпюр умножаются на найденное значение соответствующего неизвестного, и все результаты суммируются (по отдельным точкам осей системы) с добавлением к ним ординат грузовой эпюры моментов.

1.4 Построение эпюр поперечных и продольныхсил.

После того как решением системы канонических уравнений найдены неизвестные усилия Х_i , эти усилия и заданная внешняя нагрузка могут быть приложены к основной системе. Затем от их совместного действия обычным способом (как в статически определимых системах) могут быть определены поперечные и продольные силы, и построены эпюры N, Q .

Поперечные силы в статически неопределимой системе могут быть определены и другим путем – по окончательной эпюре изгибающих моментов и условия равновесия вырезанных стержней. Каждый стержень рамы рассматривается как простая статически определимая балка на двух опорах, с приложенными к ней изгибающими моментами, взятыми с окончательной эпюры изгибающих моментов и заданной внешней нагрузкой. Для каждой такой балки, в отдельности, строится эпюра поперечных сил. Потом все участки собираются на раму в целом. Поперечная сила считается положительной, если она дает момент от конца стержня на узел по часовой стрелке, и наоборот.

По эпюре поперечных сил и условия равновесия вырезанных узлов рамы строится эпюра продольных сил N. Для этого к вырезанным узлам прикладывают поперечные и продольные силы. При этом, продольные силы считаем положительными, т.е. направленными от узла. Поперечные силы прикладываются к узлу с учетом полученных значений и знаков. ( см. по полученной эпюре поперечных сил). К узлу необходимо не забывать прикладывать и внешние силы, если они непосредственно действуют на этот узел. Проектируя приложенные к узлу силы на оси координат, получим два уравнения равновесия:

S Х = 0, S Y = 0

из которых, зная поперечные силы Q, найдем продольные силы N.

Начинать определение продольных сил надо с тех узлов, в которых сходятся не более двух стержней с неизвестными продольными силами.

роверки.

Важнейшим элементом расчета рам является различные проверки на каждом этапе расчета.

1) Проверка единичных коэффициентов и свободных членов канонических уравнений. Коэффициенты и свободные члены канонических уравнений представляют собой перемещения, полученные путем перемножения соответствующих эпюр изгибающих моментов. При перемножении эпюр могут быть допущены ошибки, в результате которых значения лишних неизвестных получатся неверными. Ошибки, сделанные при подсчете перемещений, могут быть обнаружены при помощи особых проверок:

а) построчная проверка (проверяются единичные коэффициенты одной

строки – одного уравнения):

δ_is = δ_i1 + δ_i2 + δ_i3 + … + δ_in = δ_ij ,

δ_is =

М_S = М₁ + М₂ + М₃ + … + М_n

М_S - называется суммарной единичной эпюрой изгибающих моментов.

Строится в основной системе от действия одновременно всех лишних

неизвестных, равных единице. Или путем суммирования всех

единичных эпюр.

б) универсальная проверка (проверяются одновременно все единичные

коэффициенты):

δ_ss = δ_1s + δ_2s + δ_3s + … + δ_ns = δ_{i j} ,

δ_ss =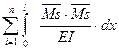

в) постолбцовая проверка (проверяются свободные члены –

коэффициенты одного столбца):

Δ_iР = Δ_1Р +Δ_2Р +Δ_3Р +…+ Δ_nР = Δ_SР , Δ_SР =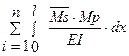

2) Проверки правильности построения окончательной эпюры изгибающих моментов:

а) Статическая проверка – основана на условии равновесия

окончательных моментов во всех узлах рамы

S М = 0

б) Деформационная проверка – заведомо нулевые перемещения в

заданной системе должны получиться равными нулю и при расчете

эквивалентной системы.

Δ_iок =

3) Статическая проверка рамы в целом – проверяется рассчитанная рама

с учетом найденных опорных реакций, изгибающих моментов,

поперечных и продольных сил через уравнения статики:

S М_F = 0, S Y = 0, S X = 0

Точку F лучше всего подбирать на раме таким образом, чтобы через нее

проходило как можно меньше найденных реакций.

Последовательность выполнения расчетно-графической работы

«Расчет плоской статически неопределимой рамы методом сил»

1. Определить степень статической неопределимости заданной рамы.

2. Выбрать основную систему метода сил и назначить лишние неизвестные усилия. Показать эквивалентную систему.

3. Составить систему канонических уравнений для определения неизвестных усилий от заданной внешней нагрузки.

4. В основной системе построить единичные эпюры изгибающих моментов М _i от действия сил Х _i =1 и грузовую эпюру М _p от действия заданной внешней нагрузки.

5. Вычислить коэффициенты и свободные члены канонических уравнений по формулам Мора.

6. Проверить полученные коэффициенты, построив суммарную

единичную эпюру изгибающих моментов и вычислив сумму всех

единичных перемещений ( универсальная проверка ).

7. Проверить полученные свободные члены, вычислив сумму свободных членов , построив суммарную единичную эпюру (постолбцовая проверка).

8. Решить систему канонических уравнений методом Гаусса и найти значения неизвестных сил Х _i . Провести проверку найденного решения, подставив найденные значения в канонические уравнения.

9. Построить окончательную эпюру изгибающих моментов по формуле:

М_ок = М_i·Х _i + М_Р

10. Проверить правильность построения окончательной эпюры:

а) Сделать статическую проверку.

б) Выполнить деформационную проверку.

Если полученная величина Δ_iок отлична от нуля, то относительная погрешность вычислений не должна превышать 3%.

11. Построить окончательную эпюру поперечных сил, используя окончательную эпюру изгибающих моментов и условия равновесия каждого вырезанного из каркаса стержня.

12. Построить окончательную эпюру продольных сил, используя окончательную эпюру поперечных сил и условие равновесия вырезанных узлов рамы.

13. Проверить статическое равновесие рамы в целом под действием заданной внешней нагрузки и опорных реакций.

Пример расчета плоской статически