Вычисление определителя матрицы и
Получение обратной матрицы
Задание. Вычислить определитель матрицы А.
Найти матрицу, обратную А.
GПримечание. Напоминание из математики по поводу операций с матрицами и векторами здесь и далее не будет, т.к. потребуется более объёмный пояснительный текст. Для воспоминаний отсылаем к [ 5 ].
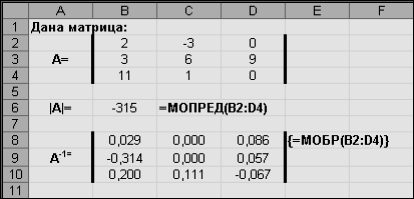
Рис.18. Выполнение
задания 6.1.
Методические указания к выполнению задания
1.Ввести в блок В2:D4 исходную матрицу.
2.Ввести формулу в В6: = МОПРЕД(В2:D4) для вычисления определителя (Категория†Математические†МОПРЕД).
3.Ввести формулу массива: {=МОБР(B2:D4)}в блок В8:D10 для получения обратной матрицы (Категория†Математические†МОБР).
4.Варианты заданий по этой теме см. 6.2.1.
6.2.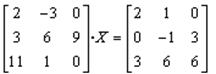 
Решение матричных уравнений
Задание. Решить матричное уравнение:
Методические указания к выполнению задания
1.Заданное матричное уравнение имеет вид A×X=B, откуда решение: X=A-1×B.
2.Ввести матрицу А в блок B1:D3 (рис.19); матрицу В – в блок B5:D7; задать имена указанным блокам.
3.Ввести в блок G3:I5 табличную формулу для Х:{=МУМНОЖ(МОБР(A);B)} .
4.Выполнить проверку: А×Х=В: ввести в блок К3:М5 табличную формулу: {=МУМНОЖ(A; G3:I5)}. Решение ( матрица Х) верно, т.к. полученная проверкой матрица совпадает с исходной матрицей В.
5.Варианты заданий по этой теме см. 6.2.2.
Рис.19. Решение матричного уравнения (пример 6.2.)
6.2.1. Варианты заданий по теме:
«Вычисление определителя матрицы и обратной матрицы»
| № | задание | № | задание | № | задание | № | задание |
 |  |  |  | ||||
 |  |  |  | ||||
 |  |  |  | ||||
 |  |  |  | ||||
 |  |  |  | ||||
 |  |  |  | ||||
 |  |  | |||||
 |  |  |
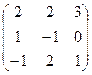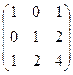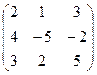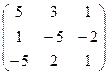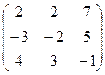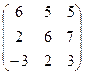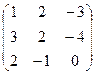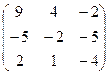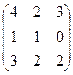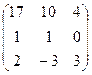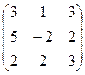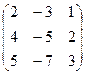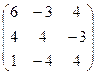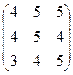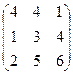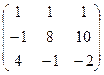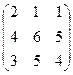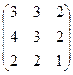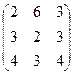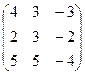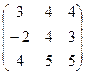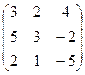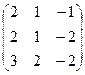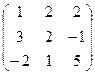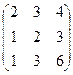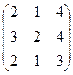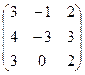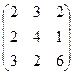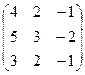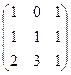6.2.2. Варианты заданий по теме: «Решение матричного уравнения»
| № | задание | № | задание | № | задание |
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  |
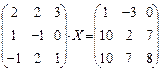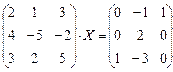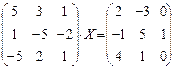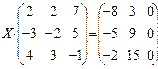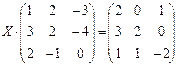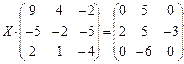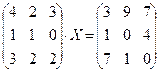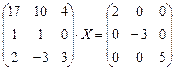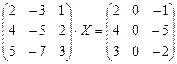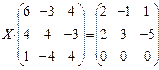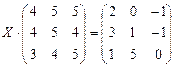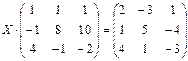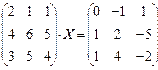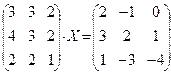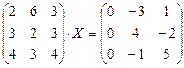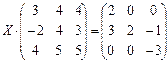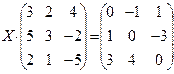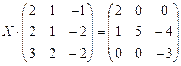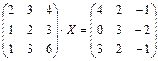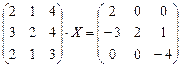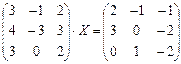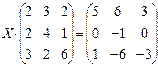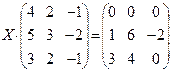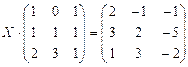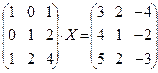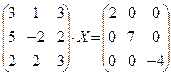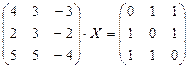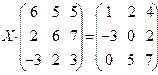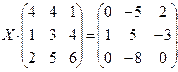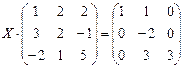Решение систем линейных уравнений
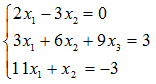методом обратной матрицы
Задание. Решить систему линейных уравнений методом обратной матрицы:
Методические указания к выполнению задания
1.Заданная система уравнений имеет вид A×X=B, откуда решение: X=A-1×B, где А – матрица коэффициентов, а В – вектор свободных членов.
2.Ввести матрицу А в блок B2:D4 (рис.20); вектор В в блок G2:G4; задать имена указанным блокам.
3.Ввести формулу массива для вектора Х: {=МУМНОЖ(МОБР(A);B)}
в блок B6:B8.
4.Выполнить проверку: А×Х=В; ввести блок F6:F8 формулу массива:
{=МУМНОЖ(A; B6:B8)}.
5.Решение – вектор Х – верное, т.к. при подстановке Х в систему уравнений получаются тождества.
6.Варианты заданий по этой теме см. 6.5.3.
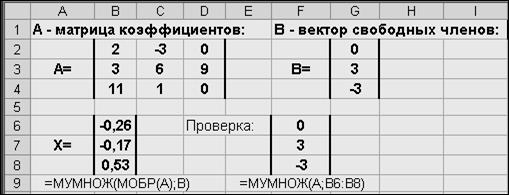
Рис.20. Решение системы линейных уравнений (пример 6.3.)
Вычисление матричных выражений
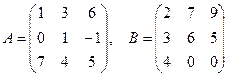Задание. Выполнить операции над матрицами:
Найти (A + B)×(A - B) -A2, где