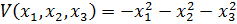F) система с типовой нелинейной характеристикой

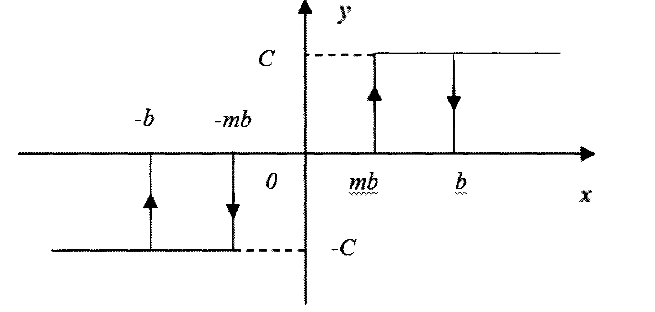
24. Типовая нелинейная характеристика соответствует следующим выражениям формулы гармонической линеаризации данной нелинейности с выходным сигналом х = 4sinωt:

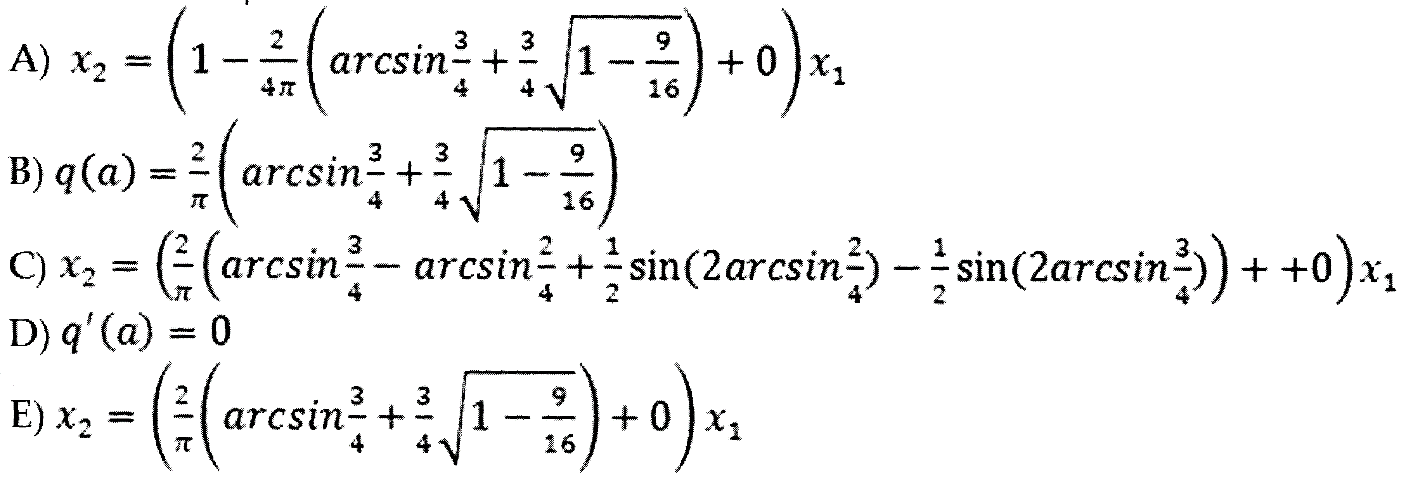
B,D,E

25. Характеристический полином нелинейной замкнутой системы после применения гармонической линеаризации имеет вид:

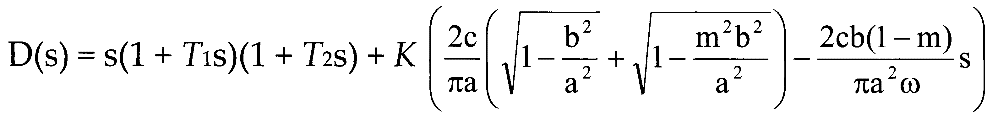тогда:

А) Действительная часть кривой Михайлова:

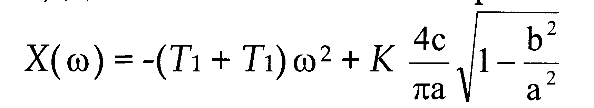
В) Мнимая часть кривой Михайлова:

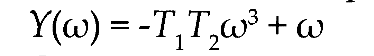
С) Мнимая часть кривой Михайлова:

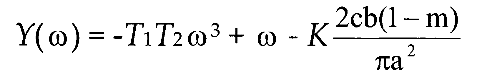
D) Кривая Михайлова соответствует выражению:

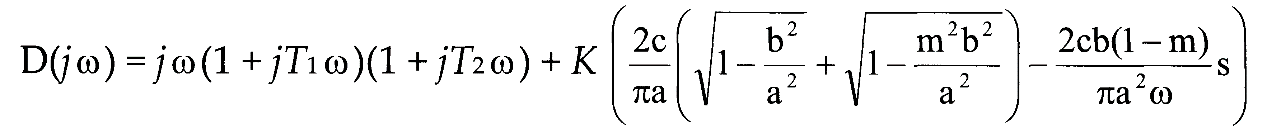
Е) Действительная часть кривой Михайлова:

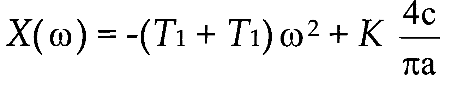
F) Кривая Михайлова соответствует выражению:

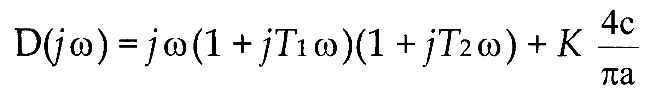
G) Кривая Михайлова соответствует выражению:

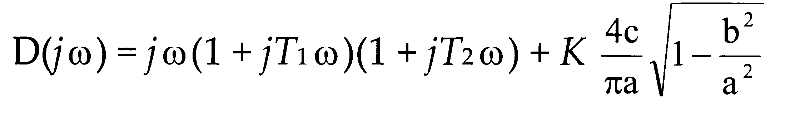
1 Приведите основные понятия, характеризующие звено с типовой характеристикой х(t)- входной сигнал, у(t)- выходной сигнал нелинейного звена):

A) линейное звено

B) трехпозиционное реле с зоной нечувствительности

C) звено со статической нелинейностью

D)линейное звено

E)трехпозиционное реле с зоной нечувствительности и гистерезисом

F)звено с зоной насыщения

2 К динамическим типовым нелинейным характеристикам относятся :

A)реле с петлей гистерезиса

B)усилитель с зоной насыщения и нечувствительности

C) усилитель с петлей гистерезиса

D) реле с зоной нечувствительности и петлей гистерезиса

E)усилитель с зоной нечувствительности

F)реле с зоной нечувствительности

3 Определите корни характеристического уравнения системы, соответствующие особой точке фазовой плоскости типа седло:

A) Комплексно-сопряженное число с положительной вещественной частью.

B) Корни, лежащие на действительной оси комплексной плоскости с различными знаками.

C)Отрицательные вещественные числа.

D)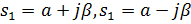

E)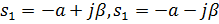

4. Типовая характеристика нелинейного звена системы с входным x(t) и выходным y(t) сигналами, соответствует выражению:

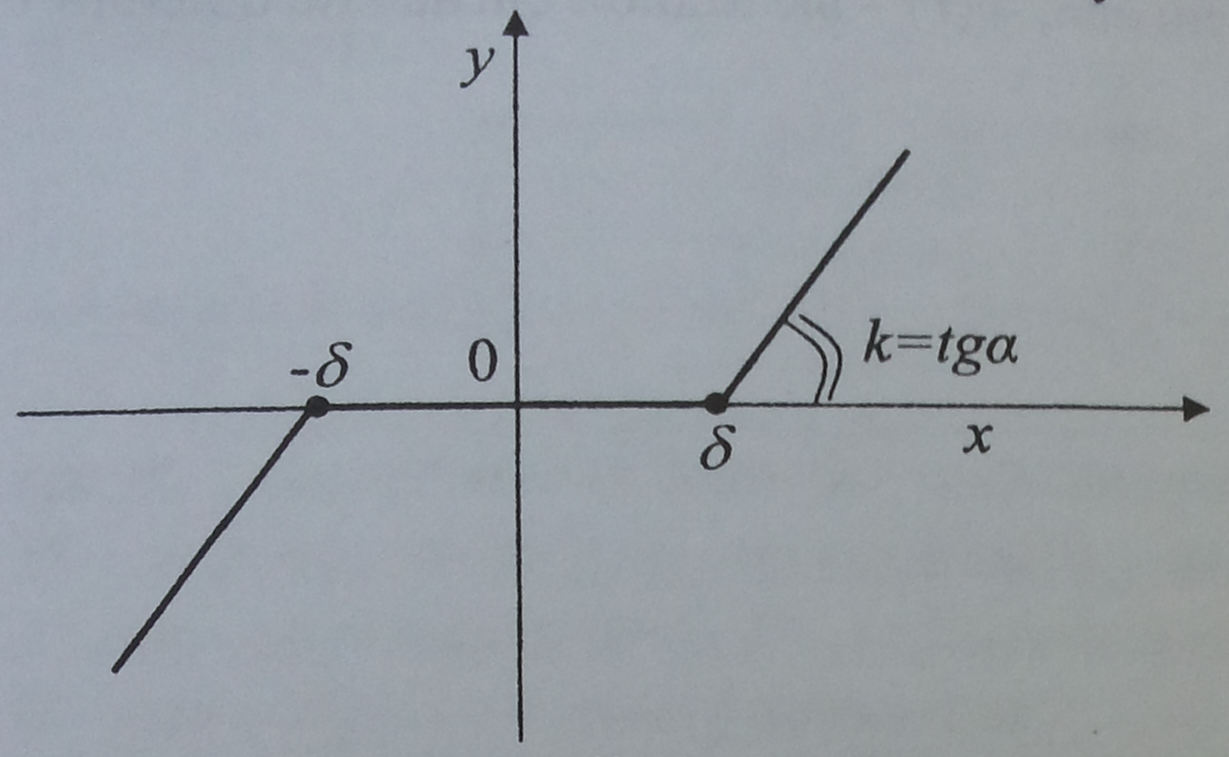
A) усилитель с зоной насыщения и нечувствительности

B) усилитель с зоной насыщения

C) усилитель с зоной нечувствительности

D) звено со статической нелинейностью

E) нелинейное звено

5. Приведите основные понятия, характеризующие звено с типовой характеристикой (x(t)- входной сигнал, y(t) – выходной сигнал нелинейного звена):

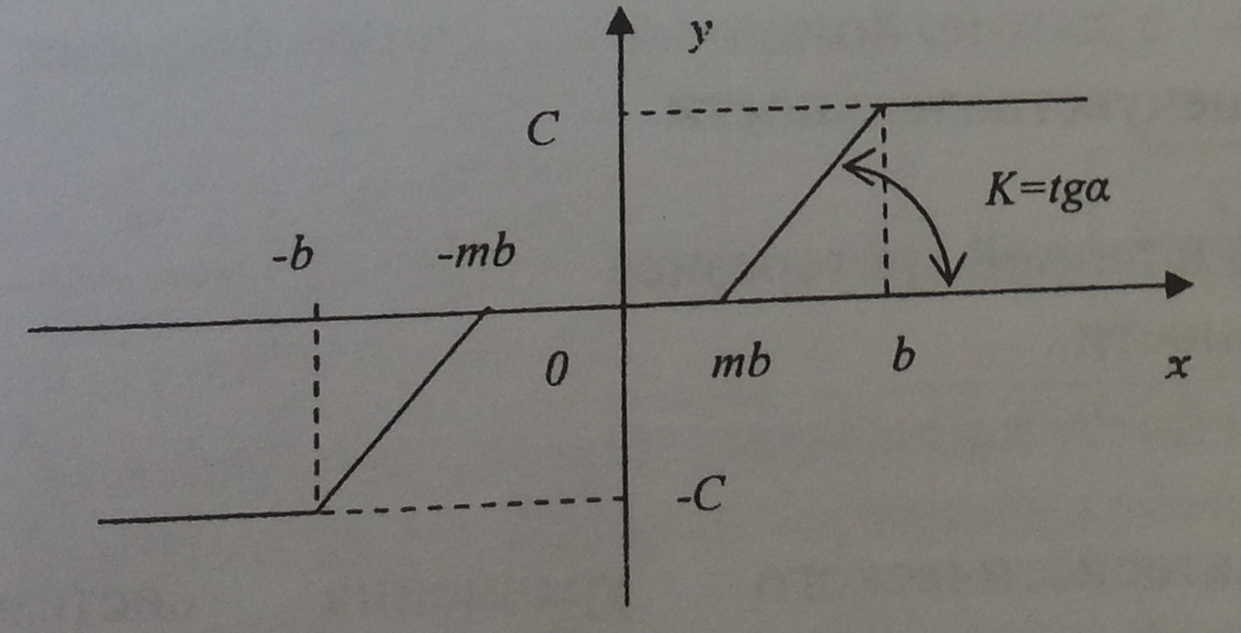
A) линейное звено

B) усилитель с зоной нечув

C) звено со статической нелинейностью

D)усилитель с зоной насыщения и нечувствительности

E)нелинейное звено

6 Задана нелинейная система с нелинейными элементами (где 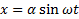) и с

передаточной функцией 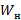(s)= 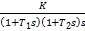, тогда на основе критерия Гольдфарба:

А) Частотная передаточная функция нелинейного звена 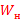(j )=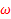

B) Частотная передаточная функция нелинейного звена: 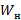(j )=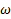

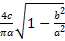
C) Годограф гармонически линеаризованного нелинейногозвена:

-Z(a)= 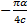( 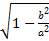-j )

)Определите корни характеристического уравнения системы, соответствующие следующему фазовому портрету:

A) =- , =-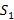

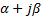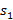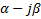
B) Корни, лежащие на действительной положительной полуоси комплексной плоскости

С) Комплексно-сопряженные числа с положительной вещественной частью.

D) =- , =-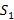

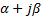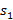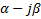
E) Корни, лежащие на действительной отрицательной полуоси комплексной плоскости

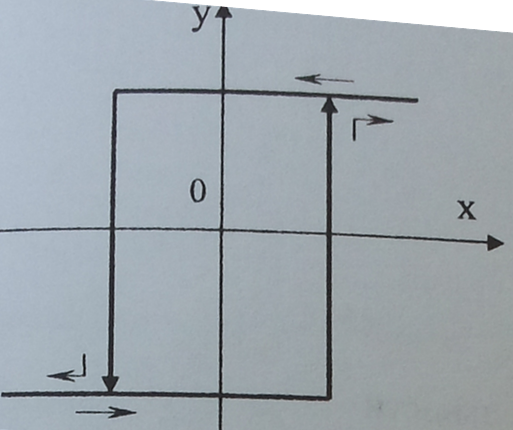
8 Фазовая траектория системы, изображенная на фазовой плоскости, соответствует:

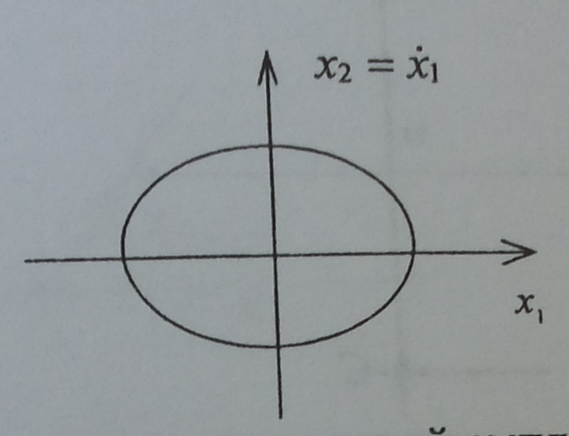
A) колебательному процессу с постоянной амплитудой и частотой

B) особой точке типа неустойчивый узел

C) дифференциальному уравнению второго порядка

D) экспоненциально сходящемуся процессу

E) экспоненциально расходящемуся процессу

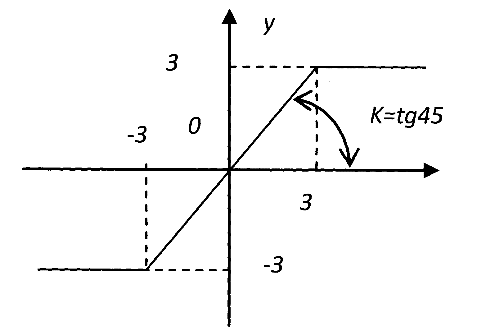
9 Определите отрицательную знакопостоянная функцию V(x₁,x₂,x₃)

A) V(x₁,x₂,x₃) = - x₁²,x₂²,x₃²

B) V(x₁,x₂,x₃) = (x₁ + x₂ + x₃)²

C) V(x₁,x₂,x₃) = -(- x₁ - x₂ + x₃)²

D) V(x₁,x₂,x₃) = -(x₁ + x₂ + x₃)²

E) V(x₁,x₂,x₃) = x₁ + x₂ + x₃

F) V(x₁,x₂,x₃) = 9 (x₁²+ x₂² + x₃²

10. Определите отрицательную знакопостоянная функции V(x₁,x₂):

А) V(x₁,x₂) = -(x₁²+2 x₁x₂ x₂²)

B) V(x₁,x₂) = 9(x₁²+x₂²)

C) V(x₁,x₂) = -(x₁+x₂)²

D) V(x₁,x₂) =(x₁,x₂)²

E) V(x₁,x₂) = - x₁² - x₂²

F)V(x₁,x₂) = 4x₁²+4x₂²

11. Определите корни характеристического уравнения системы, соответствующие следующей фазовой траектории:

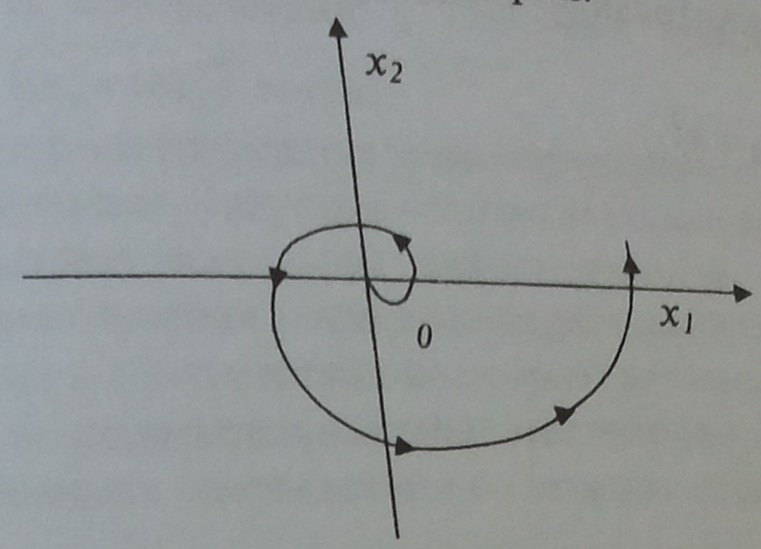
A)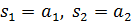

B) Отрицательные вещественные числа

C)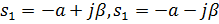

D)Комплекстно-сопряженное число с положительной вещественной частью

E) Корни, лежащие в правой полуплоскости комплексной плоскости

F) Положительные вещественные числа

12. Определите функциюV(x₁,x₂) = - x₁ - x₂ - x₃:

А) Знакопостоянная функция

B) Знакоопределенная функция

C) V(0)=0, V> 0 или V<0 в зависимости от x₁ и x₂

D) Функция в данной области вокруг начала координат может иметь разные знаки

E) Знакопеременная функция

13. Определите функцию V(x₁,x₂) = x₁² + x₂² :

A) Отрицательная знакоопределенная функция

B) Положительная знакоопределенная функция

C) V(0)=0, V ≥ 0 при x≠0

D) Функция во всех точках «-мерного пространства, исключая начало координат, сохраняет один и тот же знак и нигде не обращается в нуль, кроме самого начала координат

E) Функция сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства

14. Определите положительную знакоопределенную функцию V(x₁,x₂):

A) V(x₁,x₂) = x₁²+x₂²

B) V(x₁,x₂) = x₁²+ 2x₁x₂ +x₂²

C) V(x₁,x₂) = 4x₁²+ 4x₂²

D) V(x₁,x₂) = -x₁²-x₂²

E) V(x₁,x₂) = x₁ +x₂

F) V(x₁,x₂) = (x₁ +x₂)²

G) V(x₁,x₂) = 9(x₁² + x₂²)²

15. Для исследования устойчивости системы выбрана функция Ляпунова: V(x₁,x₂) = x₁⁴ + x₂⁴ В соответствии с системой производная от функции Ляпунова : 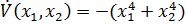тогда:

A) Функция Ляпунова отрицательная знакоопределенная

B) Функция Ляпунова положительная знакоопределенная

C) Функция Ляпунова положительная знакопостоянная

D) Система неустойчива в соответствии со вторым методом Ляпунова

E) Система устойчива в соответствии со вторым методом Ляпунова

F) Производная от функции Ляпунова - отрицательная знакопостоянная

G) Функция Ляпунова отрицательная знакопостоянная

16. Для исследования устойчивости системы выбрана функция Ляпунова: 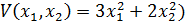. В соответствии с системой производная от функции Ляпунова: 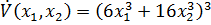гогда:

A) Функция Ляпунова и производная от функции Ляпунова не удовлетворяют второму методу Ляпунову

B) Функция Ляпунова положительная знакопостоянная

C) Производная от функции Ляпунова - знакопеременная

D) Производная от функции Ляпунова - положительная знакопостоянная

E) Функция Ляпунова отрицательная знакопостоянная

17. Для исследования устойчивости системы выбрана функция Ляпунова: 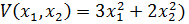.В соответствии с системой производная от функции Ляпунова: 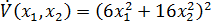тогда:

А) Функция Ляпунова положительная знакоопределенная

B) Производная от функции Ляпунова - положительная знакопостоянная

C) Функция Ляпунова положительная знакопостоянная

D) Функция Ляпунова отрицательная знакоопределенная

E) Система устойчива в соответствии со вторым методом Ляпунова

F) Функция Ляпунова отрицательная знакопостоянная

G) Система неустойчива в соответствии со вторым методом Ляпунова

18. Графики непрерывной и дискретной функций представлены на рисунках:

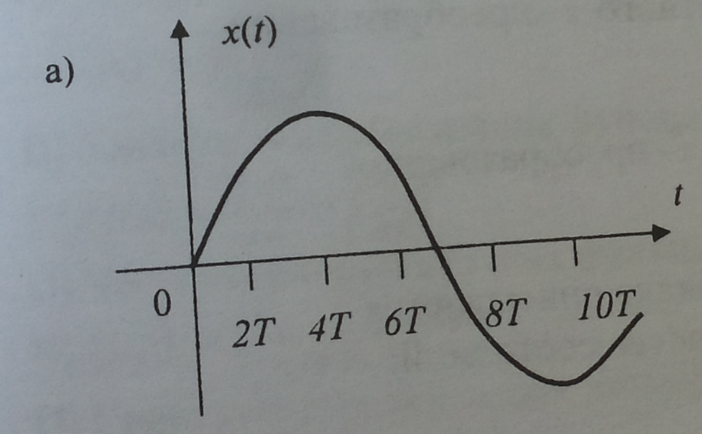
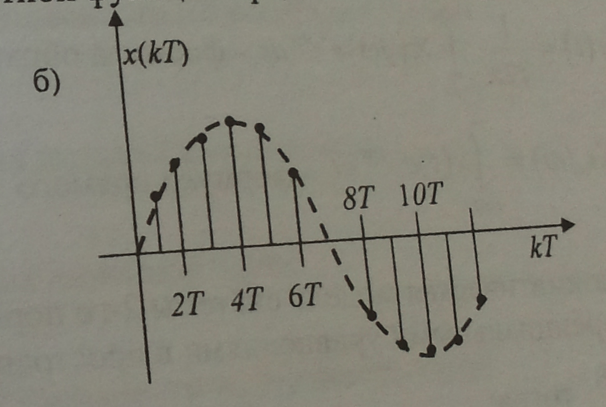
тогда:

A) 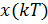– огибающая для решетчатой функции

B) 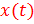– непрерывная функция

C) 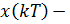непрерывная функция

D) 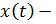решетчатая функция

E) 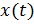– дискретная функция

F) 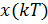- релейная характеристика

19. В основе метода z-преобразования лежат формулы:

A) 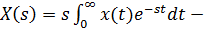формула прямого z -преобразования

B) 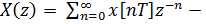формула прямого z -преобразования

C) 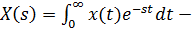формула прямого z -преобразования

D) 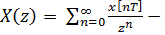формула прямого z -преобразования

E) 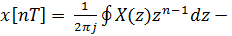формулаобратного z -преобразования

F) 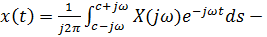формулаобратного z -преобразования

G) 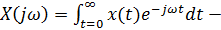формулапрямого z -преобразования

20. Математическая модель системы 2-го порядка описывается дифференциальными уравнениями в пространстве состояний:

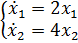тогда:

А) корни характеристического уравнения

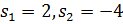
B) характеристическое уравнение

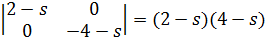
С) характеристическое уравнение

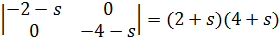
D) корни характеристического уравнения

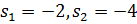
E) характеристическое уравнение

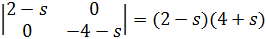
F) особая точка типа устойчивый узел

21. Задана нелинейная система с нелинейным элементом (где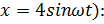

и линейным звеном с передаточной функцией 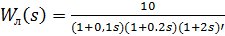тогда на основе критерия Гольдфарба:

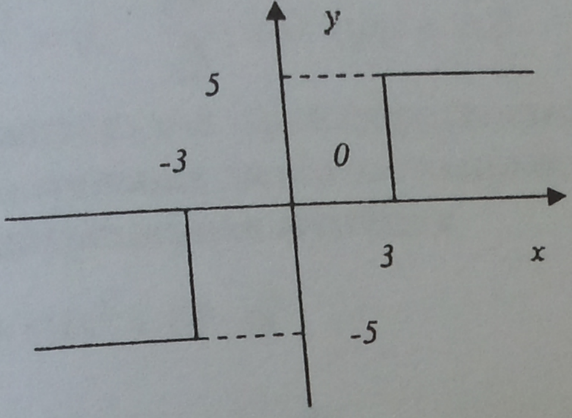
A) Годограф гармонически линеаризованного нелинейного звена:

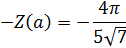
В) Частотная передаточная функция нелинейного звена:

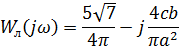
С) Частотная передаточная функция линейной части:

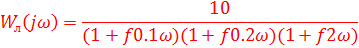
D) Годограф гармонически линеаризованного нелинейного звена:

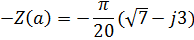
E) Годограф гармонически линеаризованного нелинейного звена: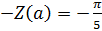

F) Частотная передаточная функция нелинейного звена: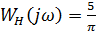

G) Частотная передаточная функция линейной части:

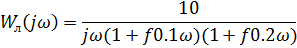
22. Задана нелинейная система с нелинейным элементом (где 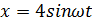и линейным звеном с передаточной функцией, 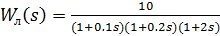тогда на основе критерия Гольдфарба:

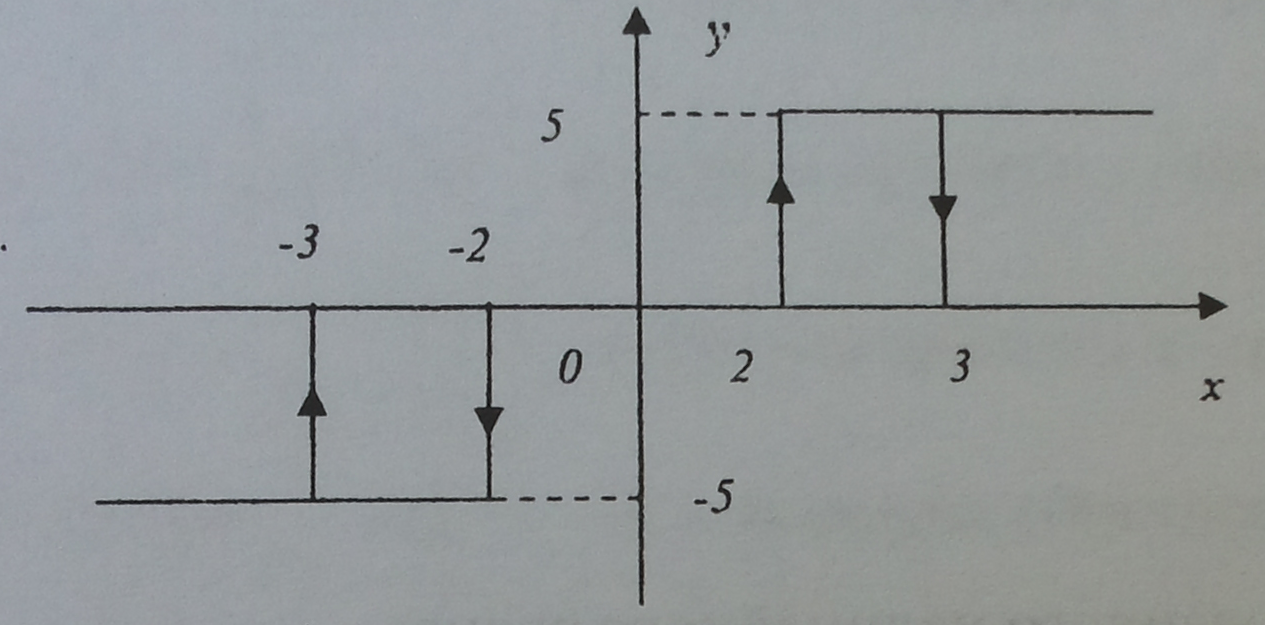
А) Годограф гармонически линеаризованного нелинейногозвена: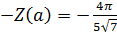

B) Частотная передаточная функция нелинейного звена: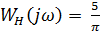

C) Частотная передаточная функция нелинейного звена: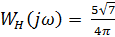

D) Частотная передаточная функция линейной части:

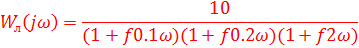
Е) Годограф гармонически линеаризованного нелинейного звена:

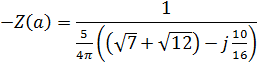
F) Частотная передаточная функция нелинейного звена:

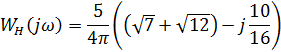
23. В соответствии с теоремой Ляпунова об устойчивости, производная отфункции Ляпунова 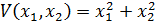нелинейной системы 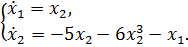соответствует выражению:

А)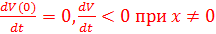

B) Положительная знакоопределенная фикция

C) Отрицательная знакопостоянная функция

D) Знакопеременная функция

E)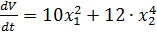

F)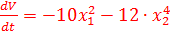

G) Отрицательная знакоопределеннаяфункция

24. В соответствии с теоремой Ляпунова о неустойчивости, производная от функции Ляпунова нелинейной системы 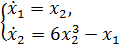соответствует выражению:

А) Отрицательная знакопостояннаяфункция

B)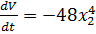

соответствует выражению.

C)Отрицательнаязнакоопределенная функция

D) Положительная знакопостояннаяфункция

E)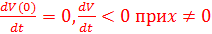

F)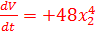

G) Знакопеременная функция

25. Задана нелинейная система с нелинейным элементом (где 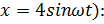и линейным звеном с передаточной функцией, 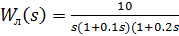тогда:

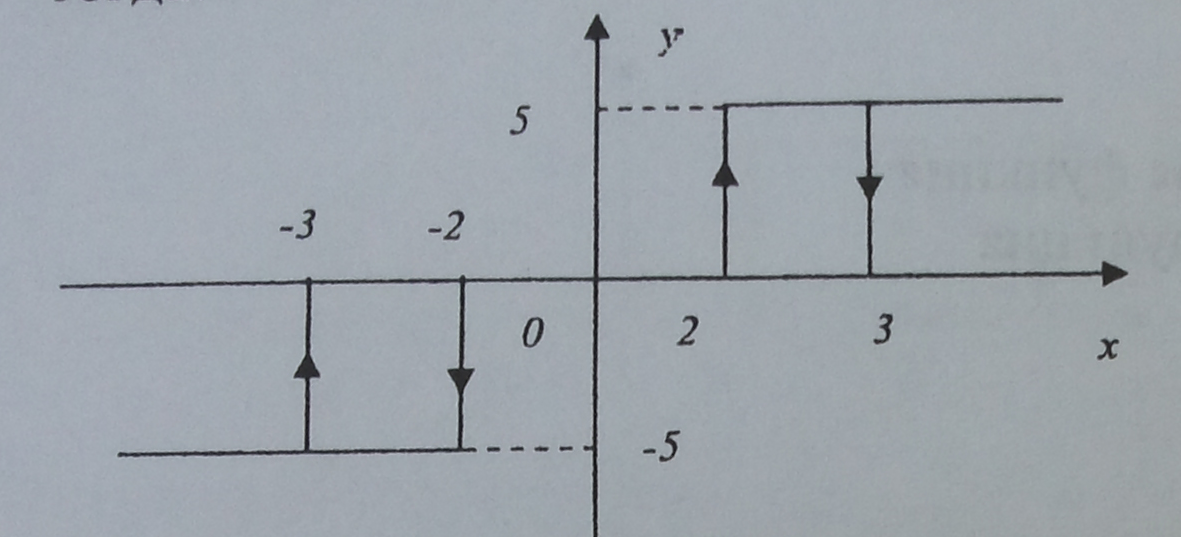
A) передаточная функция разомкнутой системы: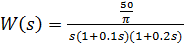

B) передаточная функция замкнутой системы:

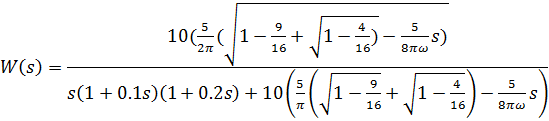
C) передаточная функция разомкнутой системы:

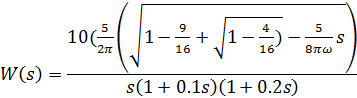
D) характеристический замкнутой системы:

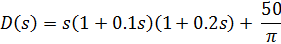
E) передаточная функция замкнутой системы:

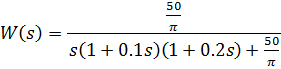
F) передаточная функция замкнутой системы

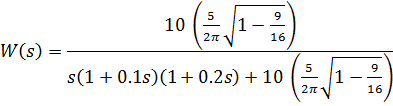
G) передаточная функция разомкнутой системы:

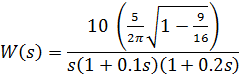
1. Определите корни характеристического уравнения системы соответствующей особой точке фазовой плоскости типа неустойчивый фокус.

A) Положительные вещественные числа

B) ,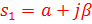

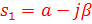
C) ,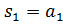

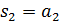
D) ,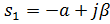

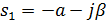
E) Отрицательные вещественные числа

2. К статистическим типовым нелинейным характеристикам относятся:

A) реле с зоной нечувствительности – статическое

B) реле с зоной нечувствительности и петлей гестерезиса

C) нелинейное трение

D) двухпозиционные реле

E) усилитель с зоной насыщения

F) усилитель с зоной нечувствительности

3. Определите корни характеристического уравнения, соответствующей особой точке фазовой плоскости типа неустойчивый узел

A) ,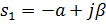

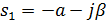
B) ,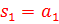

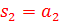
C) комплексно сопряженные числа с положительной вещественной частью

D) корни, лежащие на действительной отрицательной полуоси комплексной плоскости

E) отрицательные вещественные числа

4. Определите корни характеристического уравнения, соответствующей особой точке фазовой плоскости типа устойчивый узел

A) комплексно сопряженные числа с положительной вещественной частью

B) ,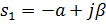

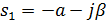
C) ,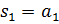

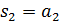
D) корни, лежащие на действительной отрицательной полуоси комплексной плоскости

E) отрицательные вещественные числа

5. Корни характеристического уравнения системы изображенной на комплексной плоскости

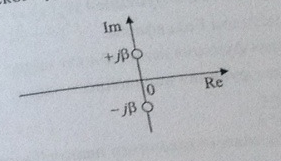соответствуют:

A) особой точке типа устойчивый узел

B) дифференцированному уравнению второго порядка

C) дифференцированному уравнению первого порядка

D) особой точке типа седло

E) экспоненциально сходящемуся процессу

F) особой точке типа устойчивый фокус

6. Фазовый портрет системы, изображенный на фазовой плоскости соответствует:

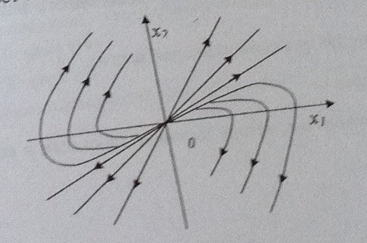
A) особой точке типа устойчивый узел

B) особой точке типа седло

C) особой точке типа неустойчивый узел

D) экспоненциально сходящемуся процессу

E) экспоненциально расходящемуся процессу

F) особой точке типа центр

7. Задана нелинейная система с нелинейным элементом (где 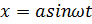) 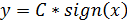и линейным звеном с передаточной функцией 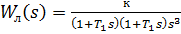тогда в соответствии с методом Гольдфарба

A) Частотная передаточная функция нелинейного звена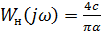

B) Частотная передаточная функция нелинейного звена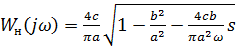

C) Годограф гармонически линеаризованного нелинейного звена: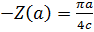

D) Годограф гармонически линеаризованного нелинейного звена: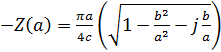

E) Частотная передаточная функция линейной части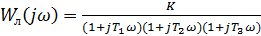

F) Годограф гармонически линеаризованного нелинейного звена: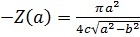

G) Частотная передаточная функция линейной части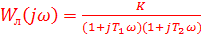

8. Приведите основные понятия метода фазовой плоскости в соответствии с рисунком:

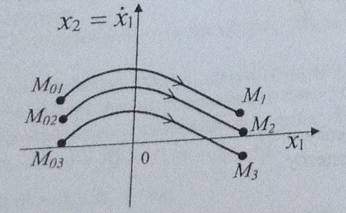
A) импульсная характеристика

B) фазовый портрет

C) фазовая плоскость

D) комплексная плоскость

E) частотная характеристика

F) переходный процесс

9. Определите знакопеременную функцию: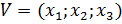

A)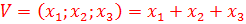

B)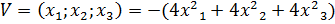

C)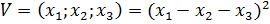

D)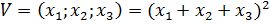

E)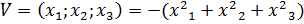

F)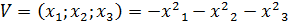

10. Определите функцию: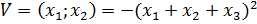

A) Отрицательная знакопостоянная функция

B) Отрицательная знакоопределенная функция

C) Функция во всех точках n-мерного пространства, исключая начало координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме самого начала координат

D) Функция сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства

E)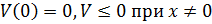

F)

G) Положительная знакоопределенная функция

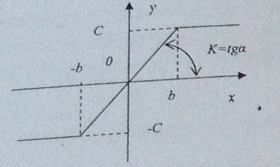
11. Задана нелинейная система с нелинейным элементом (где 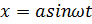) 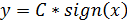и линейным звеном с передаточной функцией 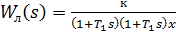тогда на основе критерия Гольдфарба

A) Годограф гармонически линеаризованного нелинейного звена:

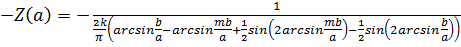
B) Частотная передаточная функция линейной части: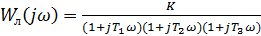

C) Частотная передаточная функция нелинейного звена

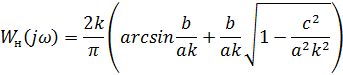
D) Годограф гармонически линеаризованного нелинейного звена

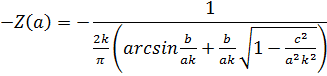
E) Частотная передаточная функция линейной части:

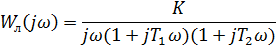
12. Следующий фазовый портрет соответствует:

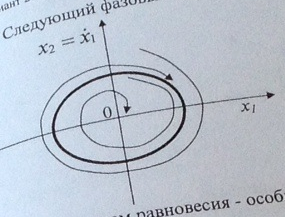
A) двум точкам равновесия – особым точкам типа устойчивый и неустойчивый центр

B) полуустойчивый предельный цикл

C) особой точке устойчивый узел

D) устойчивый предельный цикл

E) особой линии предельный цикл

13. Определите корни характеристического уравнения системы, соответствующие следующей фазовой траектории

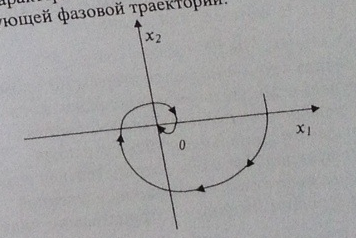
A) ,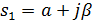

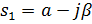
B) Отрицательные вещественные числа

C) Положительные вещественные числа

D) корни, лежащие в левой полуплоскости, комплексной плоскости

E) корни, лежащие в правой полуплоскости, комплексной плоскости

F) ,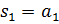

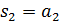
14. Фазовая траектория системы 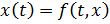, соответствует понятию

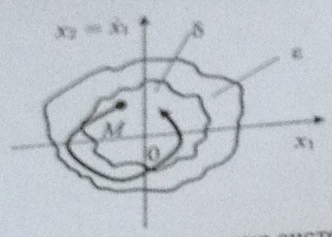
A) неустойчивости невозмущенного движения системы

B) устойчивости невозмущенного движения системы

C) абсолютной устойчивости

D) устойчивости установившегося процесса работы системы

E) асимптотической устойчивости системы в целом

F) устойчивости по Ляпунову, невозмущенного движения

G) абсолютной неустойчивости

15. Для исследования устойчивости системы выбрана функция Ляпунова: 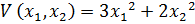. В соответствии с системой производная от функции Ляпунова: 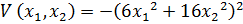, тогда:

A) система устойчива в соответствии со вторым методом Ляпунова

B) функция Ляпунова отрицательная знакоопределенная

C) функция Ляпунова положительная знакопостоянная

D) функция Ляпунова отрицательная знакопостоянная

E) производная от функции Ляпунова – отрицательная знакопостоянная

F) функция Ляпунова положительная знакоопределенная

G) производная от функции Ляпунова – отрицательная знакоопределенная

16. Для исследования устойчивости системы выбрана функция Ляпунова: 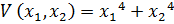. В соответствии с системой производная от функции Ляпунова: 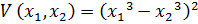, тогда:

A) производная от функции Ляпунова – отрицательная знакоопределенная

B) функция Ляпунова положительная знакоопределенная

C) функция Ляпунова отрицательная знакопостоянная

D) производная от функции Ляпунова – положительная знакопостоянная

E) система устойчива в соответствии со вторым методом Ляпунова

F) функция Ляпунова отрицательная знакоопределенная

17. Для исследования устойчивости системы выбрана функция Ляпунова: 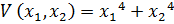. В соответствии с системой производная от функции Ляпунова: 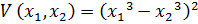, тогда: (Уравнения указаны неправильно т.к. ничего не видно)

A) функция Ляпунова положительная знакоопределенная

B) система устойчива в соответствии со вторым методом Ляпунова

C) функция Ляпунова положительная знакопостоянная

D) производная от функции Ляпунова – положительная знакоопределенная

E) функция Ляпунова отрицательная знакопостоянная

18. Квадратичная форма функции Ляпунова имеет вид 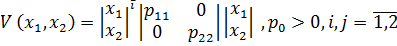, тогда:

A) 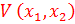- функция Ляпунова положительная знакоопределенная

B) 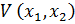- функция Ляпунова отрицательная знакоопределенная

C)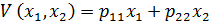

D)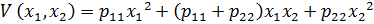

E)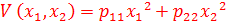

F) матрица 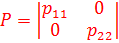- положительная знакоопределенная

19. Типовая нелинейная характеристика соответствует следующим выражениям формулы гармонической линеаризации данной нелинейности с входным сигналом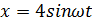

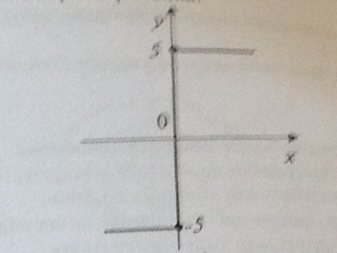
A)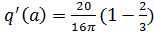

B)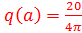

C)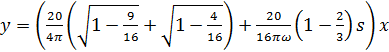

D)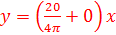

E)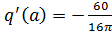

F)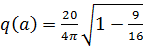

G)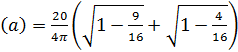

21. В соответствии с теоремой Ляпунова об устойчивости, производная от функции Ляпунова 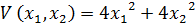нелинейной системы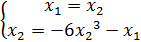

A) знакопеременная функция

B)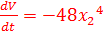

C) положительная знакопостоянная функция

D)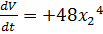

E) отрицательная знакоопределенная функция

F) отрицательная знакопостоянная функция

G) положительная знакоопределенная функция

22. Задана нелинейная система с нелинейным элементом, (где 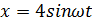) и линейным звеном с передаточной функцией 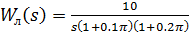тогда на основе критерия Гольдфарба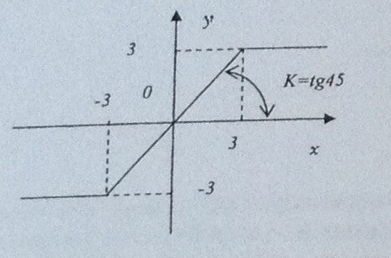

A) Годограф гармонически линеаризованного нелинейного звена:

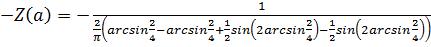
B) Годограф гармонически линеаризованного нелинейного звена:

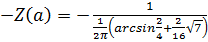
C) Частотная передаточная функция нелинейного звена

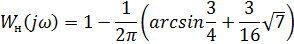
C) Годограф гармонически линеаризованного нелинейного звена:

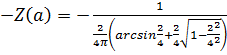
E) Частотная передаточная функция нелинейного звена

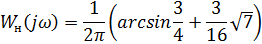
23. Математическая модель системы второго порядка описывается дифференциальными уравнениями в пространстве состояний

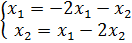, тогда

A) характеристическое уравнение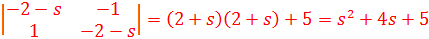

B) особая точка типа неустойчивый фокус

C) особая точка типа устойчивый фокус

D) корни характеристического уравнения ,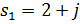

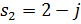
E) характеристическое уравнение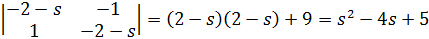

F) корни характеристического уравнения ,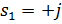

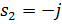
G) характеристическое уравнение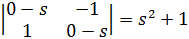

1. Корни характеристического уравнения системы, изображенные на комплексной плоскости:

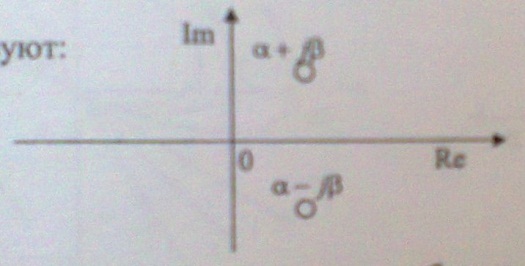
соответствуют:

А) экспоненциально сходящемуся колебательному процессу

B) особой точке типа устойчивый фокус

C) экспоненциально расходящемуся колебательному процессу

D) 0

E) особой точке типа цент

2. Приведите основные понятия, характеризующие звено с типовой характеристикой (x(t)- входной сигнал, y(t) – выходной сигнал нелинейного звена):

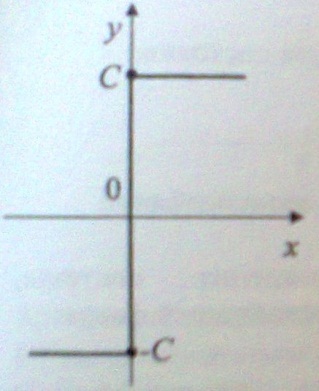
А) идеальное реле

B) усилитель с зоной насыщения

C) звено с динамической нелинейностью

D) звено со статической нелинейностью

E) трехпозиционные реле с заной нечувствительности

3. Приведите основные понятия, характеризующие звено с типовой характеристикой (x(t)- входной сигнал, y(t) – выходной сигнал нелинейного звена):

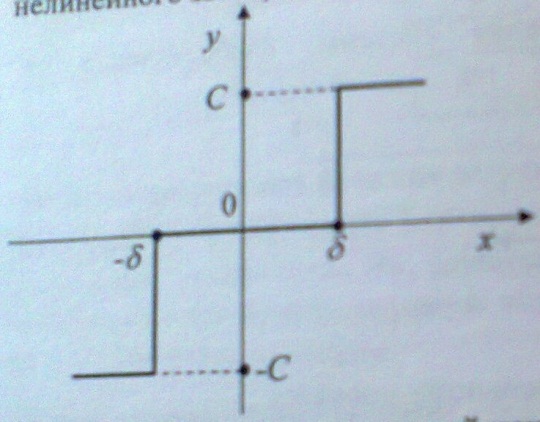
А) трехпозиционные реле с заной нечувствительности и гистерезисом

B) звено с релейной характеристикой

C) двухпозиционные реле с гистерезисом

D) идеальное реле

E) звено с зоной насыщения

F) звено с динамической налинейностью

4. Существенные особенности нелинейных систем:

А) в системе есть нелинейное звено

B) на плоскости параметров системы могут быть только два состояния системы – устойчивости и неустойчивости

C) все звенья в системе - линейные

D) неприменим принцип суперпозиции

E) на плоскости параметров системы существует области автоколебаний

5. Определите, корни характеристического уравнения системы, соответствующие особой точке фазовой плоскости типа устойчивый фокус:

А)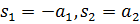

B) Положительные вещественные числа

C) Комплексно-сопряженное число с отрицательной вещественной частью

D)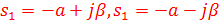

E) Корни, лежащие в левой полуплоскости комплексной плоскости

F) Корни, лежащие в правой полуплоскости комплексной плоскости

G)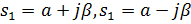

6. Фазовый портрет системы, изображенный на фазовой плоскости, соответствует:

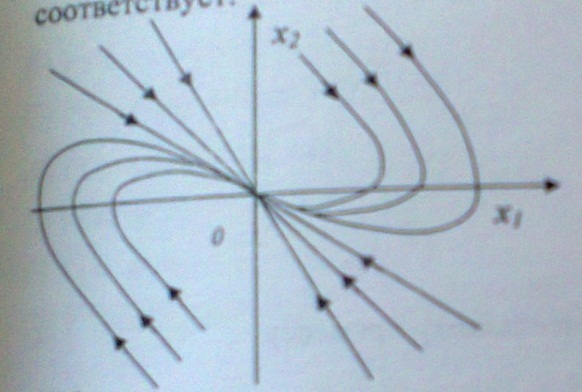
А) 0

B) особой точке типа цент

C) экспоненциально сходящемуся процессу

D) экспоненциально расходящемуся колебательному процессу

E) экспоненциально сходящемуся колебательному процессу

F) особой точке типа неустойчивый узел

7. Фазовый траектория системы, изображенный на фазовой плоскости, соответствует:

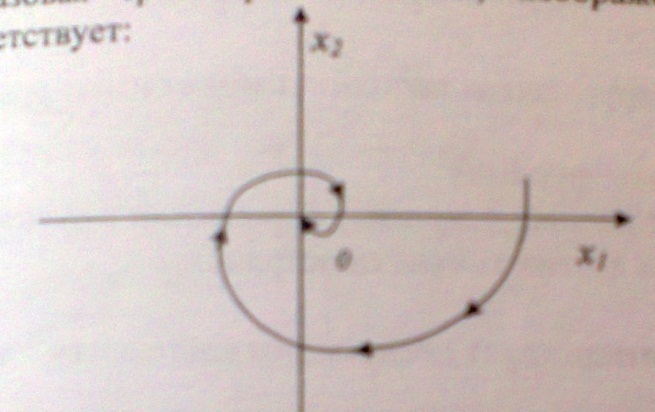
А) экспоненциально сходящемуся процессу

B) экспоненциально расходящемуся колебательному процессу

C) дифференциальному уравнению второго порядка

D) экспоненциально сходящемуся колебательному процессу

E) особой точке типа устойчивый фокус

8. Фазовый траектория системы, изображенный на фазовой плоскости, соответствует:

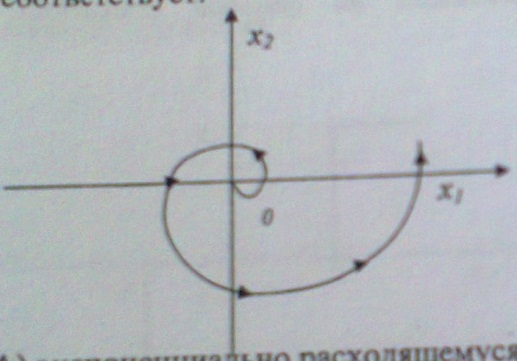
А) экспоненциально расходящемуся колебательному процессу

B) особой точке типа устойчивый фокус

C) экспоненциально сходящемуся процессу

D) дифференциальному уравнению второго порядка

E) особой точке типа неустойчивый фокус

9. Определите функцию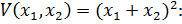

А) Положительная знакоопределенная функция

B) Отрицательная знакоопределенная функция

C)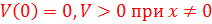

D) Функция в данной области вокруг начала координат может иметь разные знаки

E) Положительная знакопостоянная функция

F) Функция сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства

10. Фазовый портрет системы соответствует следующим состояниям устойчивости нелинейной системы:

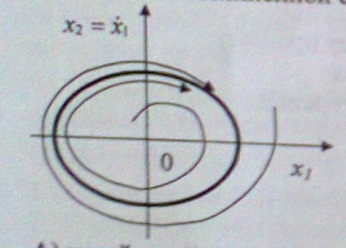
А) устойчивость «в малом» и неустойчивость «в большом»

B) устойчивый предельный цикл

C) устойчивая нелинейная система «в целом»

D) 0

E) неустойчивый предельный цикл

F) неустойчивый «в малом» и устойчивый «в большом»

11. Определите положительную знакоопределенную функцию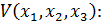

А)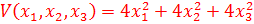

B)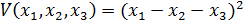

C)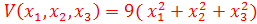

D)