Элементы комбинаторики

Глава 1. Случайные события. Вычисление вероятности

1. 1.1. Элементы комбинаторики

2. 1.2. Классическое определение вероятности

3. 1.3. Геометрическое определение вероятности

4. 1.4. Сложение и умножение вероятностей

5. 1.5. Условная вероятность

6. 1.6. Формула полной вероятности и формула Байеса

7. 1.7. Независимые испытания. Формула Бернулли

8. 1.8. Наивероятнейшее число успехов

9. 1.9. Формула Пуассона

10. 1.10. Теоремы Муавра-Лапласа

Элементы комбинаторики

Рассмотрим некоторое множество Х, состоящее из n элементов 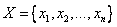. Будем выбирать из этого множества различные упорядоченные подмножества 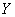из k элементов.

Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор 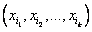элементов множества Х.

Если выбор элементов множества 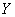из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле 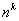(размещения с повторениями).

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается 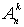и определяется равенством

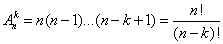
(размещения без повторений).

Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр.

Решение. Если цифры могут повторяться, то количество трехзначных чисел будет 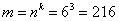. Если цифры не повторяются, то .

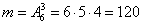Пример. Студенты института изучают в каждом семестре по десять дисциплин. В расписание занятий включаются каждый день по 3 дисциплины. Сколько различных расписаний может составить диспетчерская?

Решение. Расписание на каждый день может отличаться либо предметами, либо порядком расположения этих предметов, поэтому имеем размещения: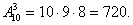

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно
.

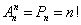Пример. 30 книг стоит на книжной полке, из них 27 различных книг и одного автора три книги. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом?

Решение. Будем считать три книги одного автора за одну книгу, тогда число перестановок будет 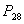. А три книги можно переставлять между собой 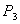способами, тогда по правилу произведения имеем, что искомое число способов равно: 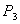* 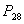=3!*28!

Пусть теперь из множества Х выбирается неупорядоченное подмножество 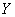(порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по kназываются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается 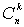и равно
.

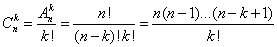Справедливы равенства: , , .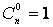

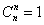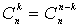Пример. В группе из 27 студентов нужно выбрать трех дежурных. Сколькими способами можно это сделать?

Решение. Так как порядок студентов не важен, используем формулу для числа сочетаний: .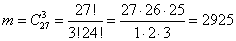

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

Пример. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка?

Решение. Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами выбор туфель. По принципу умножения получается 4*5*3=60 нарядов (комбинаций).