Алгоритм программы метода прямоугольника

Þ В качестве констант можно задать количество точек разбиения N и границы отрезка интегрирования.

Þ Шаг разбиения H определяется переменной вещественного типа, также нам понадобится вспомогательные переменная K целого типа (для оператора цикла) и переменная Integral для хранения приближенного значения интеграла. Для определения координаты точки разбиения используется переменная X вещественного типа.

Þ Подинтегральную функцию лучше всего задать в программе с помощью оператора функции Function.

Þ В начале программы следует вычислить шаг разбиения по формуле H:=(B-A)/N;

Þ Начальное значение интеграла Integral равно 0.

Þ Для вычисления приближенного значения интеграла по формуле левых прямоугольников (2.4) нам потребуется выполнить одну и ту же операцию (суммирование) заданное количество раз. Для этого можно использовать цикл с параметром. Параметр K меняется от 0 до N-1.

Þ В цикле мы должны увеличивать значение переменной Integral на .

Þ Для этого в текст программы вставим две команды. Первая считает координаты очередной точки разбиения X:=A+K*H; Вторая команда имеет вид: Integral:=Integral+F(X); Обе команды должны выполняться в цикле, поэтому их необходимо объединить в составной оператор begin .. end.

Þ Для окончательного вычисления интеграла нам необходимо умножить значение переменной Integral (в формуле это сумма элементов в квадратных скобках) на шаг разбиения: Integral:=Integral*H;

Þ Заключительный шаг алгоритма - вывести полученное решение на экран.

Формула трапеций

Формула трапеций имеет вид:

. (2.6)

Формулу трапеций проще всего получить из геометрического смысла операции интегрирования (рисунок № 4). Интеграл равен площади фигуры, ограниченной подинтегральной функцией и осями координат. Данная площадь приблизительно равна сумме площадей трапеций.

Площадь k-той трапеции равна

. (2.7)

Поэтому имеем

.

Т.е. получили формулу (2.6).

Если на отрезке 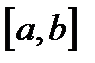существует , то для погрешности метода трапеций справедлива оценка:

. (2.8)

Т.о. формулы прямоугольников и трапеций характеризуются погрешностью одного класса[6], но погрешность у метода трапеций в 2 раза больше.

Рисунок 3. Геометрический смысл метода трапеций

Пример фрагмента программы для вычисления интеграла по формуле трапеций. Предполагается, что ранее были определены все соответствующие переменные и подинтегральная функция F(x).

H:=(B-A)/N;

Integral:=F(A)+F(B);

For K:=1 to N-1 do

begin

X:=A+K*H;

Integral:=Integral+2*F(X);

end;

Integral:=Integral*H/2;

Формула Симпсона

Для вывода формулы Симпсона заменим подинтегральную функцию 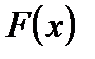на отрезке 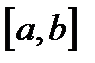некоторой вспомогательной функцией . Пусть для заданного равномерного разбиения

,

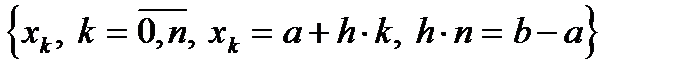причем на частичных отрезках функция является полиномом второй степени[7] .

Полиномы подберем так, чтобы выполнялись условия:

, и .

В соответствии с выбором функции имеем, что искомый интеграл приблизительно равен интегралу от функции . Зачем был сделан такой переход? Интеграл от полинома легко подсчитать...

.

Чтобы избегать работы с дробными индексами, решили ограничить значения n только четными числами и записывать формулу Симпсона в форме:

(2.9)

Примечание. Не следует забывать о важном ограничении формулы Симпсона - она работает только для четных n.

Погрешность формулы Симпсона удовлетворяет неравенству

(2.10)

при условии существования четвертой производной подинтегральной функции.

Выводы:

Þ Погрешность формулы Симпсона убывает как .

Þ Формула Симпсона точнее формул прямоугольников и трапеций.

Пример. Сравнение формул при вычислении :

Þ Формула Ньютона - Лейбница: I = Ln(2) = 0.693147

Þ Формула Прямоугольников: I = 0.692835

Þ Формула Трапеций: I = 0.693771

Þ Формула Симпсона: I = 0.693150

На практике оценка погрешности численного интегрирования с помощью формулы (2.10) является малоэффективной из-за трудностей, связанных с оценкой производной .

Обычно поступают так - берут параметр n, кратный 4. Вычисляют и . Тогда погрешность приблизительно равна[8]

. (2.11)

Алгоритм метода Симпсона похож на алгоритмы прямоугольников и трапеций. Просто при вычислении суммы элементов в круглых скобках (в цикле) следует поставить условие[9]: для четного номера точки разбиения K значение функции следует умножить на 2, а для нечетного номера на 4.

Данные три метода - Симпсона, прямоугольников и трапеций - разработаны на основе геометрической интерпретации операции интегрирования, имеют простые алгоритмы и обладают важным свойством итерационных методов: изменяя некоторый параметр (количество точек разбиения), можно существенно повысить точность расчета. Их основной недостаток: если подинтегральная функция имеет сложный вид, то ее вычисление в десятках или сотнях точек может сильно замедлить работу программы[10].

Ниже будут рассмотрены два метода приближенного интегрирования - формулы Чебышева и Гаусса. При выводе данных формул основное внимание было уделено именно скорости вычисления интеграла за счет понижения точности расчета (для некоторых классов функций). В этих методах требуется знать значение подинтегральной функции в 2 - 8 точках отрезка, но координаты этих точек выбираются строго определенным образом.