Модифицированный метод Ньютона
Модифицированный метод Ньютона основан на методе Ньютона. Если производная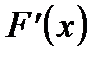 
изменяется незначительно на отрезке 
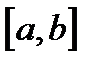, то можно предположить 
.
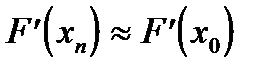Отсюда для корня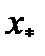 
уравнения 
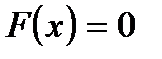получаем последовательные приближения
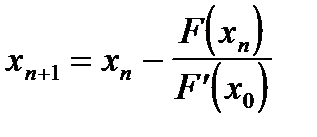, n=0,1,2... (1.16)
Геометрически этот способ означает, что мы заменяем касательные в точках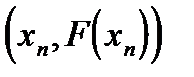 
на прямые, параллельные касательной к кривой в фиксированной точке 
.
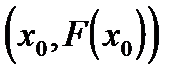Данный метод позволяет отказаться от многократного вычисления производной 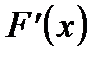в точках 
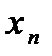. Модифицированный метод Ньютона используют для решения уравнений, в которых вычисление производной является трудоемким и относительно долговременным. В других случаях лучше применять стандартный метод Ньютона.
Ограничения на функцию и начальное приближение у модифицированного и стандартного методов Ньютона совпадают. Алгоритм обоих методов практически один и тот же.
Модифицированный метод Ньютона обладает линейной сходимостью
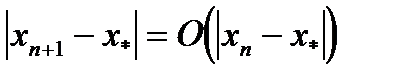. (1.17)
Метод гарантирует отсутствие деления на ноль, если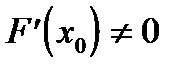 
.
Пример. Уравнение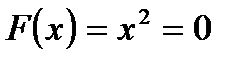 
.
Применяют метод Ньютона с параметром, т.к. корень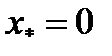 
имеет кратность p=2. Возьмем начальное приближение 
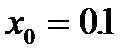и получаем 
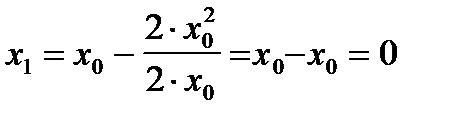. Корень найден.
Пример. Уравнение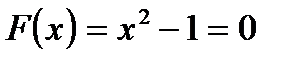 
.
Корень изолирован на отрезке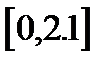 
. Погрешность Eps равна 0.000001
Метод Ньютона сходится за 5 итераций, модифицированный метод Ньютона за 19 итераций, метод половинного деления за 22 итерации. Сходимость метода итераций зависит от выбора параметра. При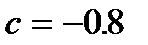 
сходимость достигается за 24 итерации, 
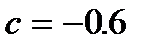сходимость за 11 итераций, 
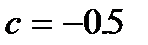сходимость за 6 итераций, 
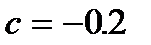сходимость за 25 итераций.
Метод секущих
Метод секущих получается из метода Ньютона заменой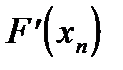 
разделенной разностью
,
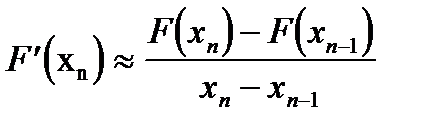вычисленной по известным приближениям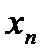 
и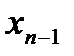 
.
Соответственно получается следующая формула метода секущих
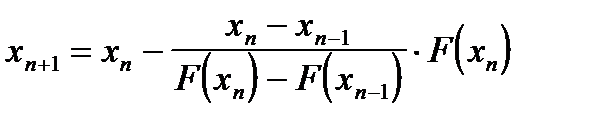. (1.18)
Данный метод является двухшаговым (т.к. надо знать два предыдущих шага для выполнения нового шага). Этим он отличается от всех ранее приведенных методов - одношаговых.
Для метода секущих вначале подбирается начальное приближение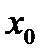 
. Далее, используя формулу другого метода или иным способом, вычисляется второе начальное приближение 
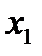. И только потом, для вычисления последующих приближений, используется формула метода секущих.
Интегрирование функций
Постановка задачи
Пусть на отрезке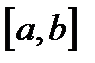 
задана непрерывная функция 
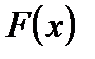. Построим разбиение отрезка точками 
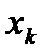на частичные отрезки:
.
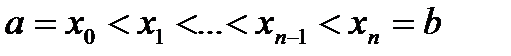Длина отрезков равна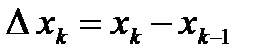 
.
Назовем интегральной сумму
,
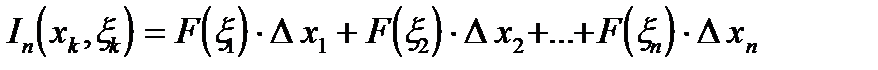где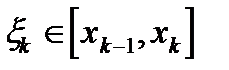 
.
Определенным интегралом функции 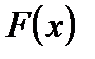на отрезке 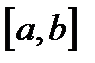называется
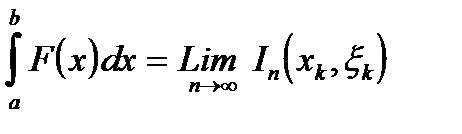. (2.1)
Классы интегрируемых функций и их свойства рассматриваются в теории математического анализа и здесь не обсуждаются. Мы будем предполагать, что наша функция является интегрируемой на отрезке .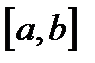
Как можно вычислить интеграл на практике? Для этого обычно используют формулу Ньютона - Лейбница:
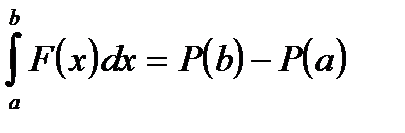, (2.2)
где P(x) - первообразная функции F(x), т.е.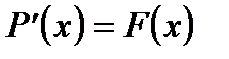 
.
Формула Ньютона - Лейбница играет большую роль в математическом анализе. Но можно ли ее применять при решении задачи на компьютере? Можно, но не всегда (т.к. первообразная не всегда существует).
Удобно ее применять при составлении программ? Нет, необходимо знать первообразную. Кроме того, если функция задана графиком или таблицей, то интеграл от нее данной формулой не вычислишь.
Это позволяет сделать вывод, что формула Ньютона - Лейбница не дает общего, универсального метода нахождения определенного интеграла от произвольной функции 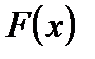и ее не рекомендуется применять в профессиональных программах для ЭВМ. Формулу Ньютона - Лейбница применяют только для проверки новых разработанных программ, в которых были реализованы другие методы приближенного интегрирования функций.
Ниже будут представлены универсальные вычислительные алгоритмы решения задачи численного интегрирования. Подобные методы позволяют подсчитывать интегралы непосредственно по значениям подинтегральной функции 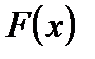и не зависят от способа ее задания.
Соответствующие формулы называют формулами численного интегрирования или квадратурными формулами[5].
В дальнейшем будем считать, если специально не будет оговорено противное, что для отрезка 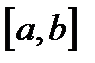мы построили равномерное разбиение с постоянным шагом h:
.
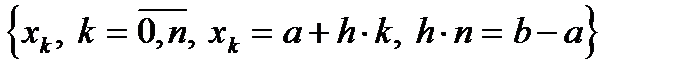Шаг разбиения в этом случае считают по формуле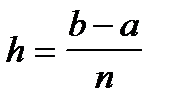 
.