Основные способы решения уравнений
Функции и графики
Основные обозначения и определения.Множество всех действительных чисел будем обозначать через R. Часто мы будем рассматривать не все множество R, а некоторые его подмножества. Тот факт, что множество А содержится во множестве R, обозначают через 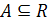 . Например, для множества всех целых чисел Z справедливо включение
. Например, для множества всех целых чисел Z справедливо включение 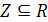 . В общем случае числовое множество А задается так:
. В общем случае числовое множество А задается так: 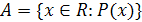 , где Р(х) — некоторое свойство, которому удовлетворяют элементы множества А и только они. Например, отрезок от 1 до 2 можно определить так:
, где Р(х) — некоторое свойство, которому удовлетворяют элементы множества А и только они. Например, отрезок от 1 до 2 можно определить так: 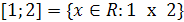 . Числовые множества связывают друг с другом посредством функций.
. Числовые множества связывают друг с другом посредством функций.
Определение. Пусть 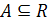 . Функцией f на множестве А будем называть правило, по которому каждому элементу
. Функцией f на множестве А будем называть правило, по которому каждому элементу 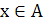 ставится в соответствие единственное число f(х) (функцию обозначают f:
ставится в соответствие единственное число f(х) (функцию обозначают f: 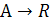 ). При этом множество А называют областью определения функции f и обозначается через D(f). Графиком функции f :
). При этом множество А называют областью определения функции f и обозначается через D(f). Графиком функции f : 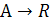 называют следующее подмножество координатной плоскости Г(f) =
называют следующее подмножество координатной плоскости Г(f) = 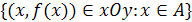 .
.
Часто правило, о котором идет речь в определении функции, является алгебраическим выражением от переменной х. В этом случае мы будем говорить, что функция задана формулой. Вспомним некоторые функции, их свойства и графики.
 Пример 1. Линейная функция задается формулой
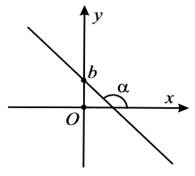
Пример 1. Линейная функция задается формулой
f(х)=kx + b. D(f)=R. Г(f) — прямая. Смысл коэффициентов k и b следующий: k = tga, где a угол наклона Г(f) к оси Ох, а b задает смещение Г(f) относительно начала координат вдоль оси Оу (проще говоря, b = f(0)). При k = 0 прямая Г(f) параллельна оси Ох.
 Пример 2. Формула
Пример 2. Формула 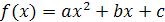 при
при 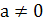
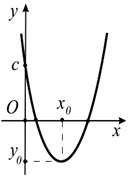
задает квадратичную функцию. D(f)=R. Г(f) -парабола.
Знак коэффициента а, как известно, указывает на
направление ветвей параболы, с = f(0) — ордината
точки пересечения параболы с осью Оу. С осью абсцисс
Г(f) пересекается только при условии 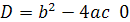
 в точках
в точках 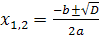 . Вершина параболы имеет координаты (х0, у0), где
. Вершина параболы имеет координаты (х0, у0), где 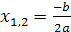 , а
, а 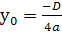 .
.
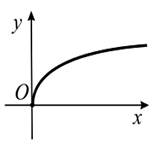
Пример 3. Областью определения квадратного корня, т.е. функции 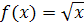 , является R+ =
, является R+ = 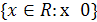 . Г(f) может быть получен симметрией относительно прямой у = х из
. Г(f) может быть получен симметрией относительно прямой у = х из
графика функции 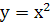 , рассмотренной на множестве R+.
, рассмотренной на множестве R+.
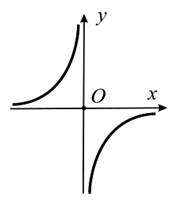 Пример 4. Функция обратной пропорциональной зависимости задается формулой
Пример 4. Функция обратной пропорциональной зависимости задается формулой 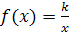 , где
, где 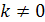 .
.  , Г(f) — гипербола, расположенная в первом и
, Г(f) — гипербола, расположенная в первом и
третьем координатных углах при при k > 0, и во втором и четвертом - k < 0.
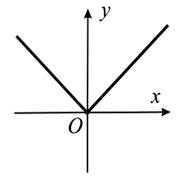 Пример 3. Функция абсолютной величины, или модуля, определяется следующим образом
Пример 3. Функция абсолютной величины, или модуля, определяется следующим образом
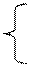 f(x) = |x| = x, если
f(x) = |x| = x, если 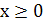 ,
,
- х, если 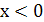 .
.
Из определения немедленно следует неравенство 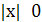 при всех
при всех 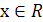 . Кроме того , при решении некоторых уравнений полезно помнить о геометрическом свойстве модуля: |x| - это расстояние на числовой прямой от х до 0.
. Кроме того , при решении некоторых уравнений полезно помнить о геометрическом свойстве модуля: |x| - это расстояние на числовой прямой от х до 0.
Основные способы решения уравнений
Уравнение с одной переменной в общем виде выглядит так:
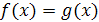 , (1)
, (1)
где 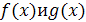 - некоторые алгебраические выражения. Областью допустимых значений (сокращенно — ОДЗ) этого уравнения называют общую часть множеств
- некоторые алгебраические выражения. Областью допустимых значений (сокращенно — ОДЗ) этого уравнения называют общую часть множеств 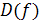 и
и 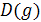 , т. е. Все такие х, для которых одновременно определены левая и правая части уравнения. Корнем уравнения (1) (или его решением) называется такое х0, что верно числовое равенство
, т. е. Все такие х, для которых одновременно определены левая и правая части уравнения. Корнем уравнения (1) (или его решением) называется такое х0, что верно числовое равенство 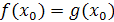 . Уравнения
. Уравнения 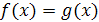 и
и 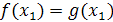 называются равносильными (обозначается факт равносильности так:
называются равносильными (обозначается факт равносильности так: 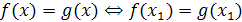 ) , если множества их решений совпадают. Например,
) , если множества их решений совпадают. Например, 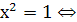 |x|=1. Рассмотрим нескольких стандартных способов решения уравнений.
|x|=1. Рассмотрим нескольких стандартных способов решения уравнений.
I. Переход к совокупности уравнений. Через А обозначим ОДЗ уравнения 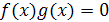 . Тогда на множестве А это уравнение равносильно совокупности уравнений
. Тогда на множестве А это уравнение равносильно совокупности уравнений 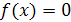 и
и 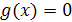 (решением совокупности является объединение решений каждого из ее уравнений). Например,
(решением совокупности является объединение решений каждого из ее уравнений). Например,
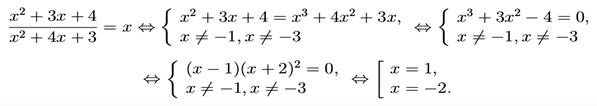
II. Замена переменной. Начнем с примера . Предположим, что нам необходимо решить уравнение
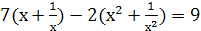 .
.
Сделаем замену 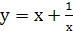 . Тогда
. Тогда 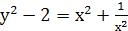 . Поэтому данное уравнение сводится к
. Поэтому данное уравнение сводится к 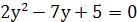 . Откуда у =1 или
. Откуда у =1 или 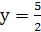 . Делая обратную замену, обнаруживаем, что корень у = 1 не дает решений относительно х, а из
. Делая обратную замену, обнаруживаем, что корень у = 1 не дает решений относительно х, а из 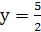 получим два искомых корня: х = 2, х =
получим два искомых корня: х = 2, х =  .
.
Итак, суть метода замены переменной в следующем: (а) выделение некоторого выражения относительно х (т. е. преобразование уравнения 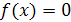 к равносильному
к равносильному 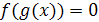 ); (б) нахождение {y1, …..yn} — множества всех решений уравнения
); (б) нахождение {y1, …..yn} — множества всех решений уравнения 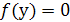 , где
, где 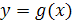 ; (в) «обратная замена», т.е. нахождение решения совокупности уравнений
; (в) «обратная замена», т.е. нахождение решения совокупности уравнений 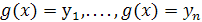 .
.
Далее рассмотрим несколько типичных иррациональных уравнений с модулем.
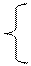 III.
III. 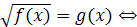
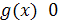 ,
,
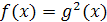 . Нетрудно заметить, что из последнего условия следует
. Нетрудно заметить, что из последнего условия следует 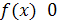 . Поэтому при решении иррационального уравнения этим методом не надо находить ОДЗ исходного уравнения. Решим уравнение
. Поэтому при решении иррационального уравнения этим методом не надо находить ОДЗ исходного уравнения. Решим уравнение
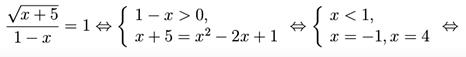
Х х = -1.
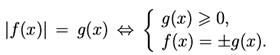 IV.
IV.
Справедливость этого метода сразу следует из геометрического свойства модуля.
Например,
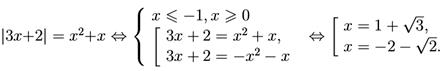
V. 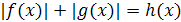 . Для решения этого уравнения достаточно воспользоваться следующим алгоритмом.
. Для решения этого уравнения достаточно воспользоваться следующим алгоритмом.
| 1. На прямой нанести нули подмодульных выражений, а также точки, в которых подмодульные выражения не определены. 2. На каждом из получившихся промежутков определить знаки подмодульных выражений. 3. В соответствии со знаками из предыдущего пункта на каждом из промежутков раскрыть модули. |
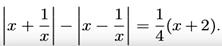 Решим уравнение Второе подмодульное выражение обращается в ноль только при
Решим уравнение Второе подмодульное выражение обращается в ноль только при 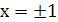 , первое всегда отлично от нуля. Кроме того, в точке х = 0 подмодульные выражения не определены. Знаки подмодульных выражений на каждом из четырех промежутков легко определяются подстановкой внутренних точек.
, первое всегда отлично от нуля. Кроме того, в точке х = 0 подмодульные выражения не определены. Знаки подмодульных выражений на каждом из четырех промежутков легко определяются подстановкой внутренних точек.
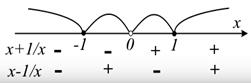
Раскроем теперь модули на каждом из промежутков.
1 случай: 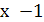 . После раскрытия модулей получим
. После раскрытия модулей получим 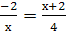 . Последнее уравнение преобразуется к уравнению
. Последнее уравнение преобразуется к уравнению 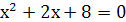 без корней.
без корней.
2 случай: 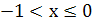 . На этом промежутке имеем
. На этом промежутке имеем 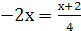 . Это уравнение имеет корень
. Это уравнение имеет корень 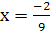 , который лежит в рассматриваемом промежутке.
, который лежит в рассматриваемом промежутке.
3 случай: 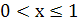 . Получаем
. Получаем 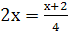 или
или 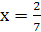 .
.
4 случай: 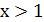 . Раскрывая модули на этом последнем промежутке, получим уравнение
. Раскрывая модули на этом последнем промежутке, получим уравнение 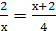 . Оно сводится к квадратному уравнению
. Оно сводится к квадратному уравнению 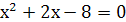 с корнями х = - 4 и х = 2. Условию
с корнями х = - 4 и х = 2. Условию 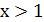 удовлетворяет только х = 2.
удовлетворяет только х = 2.
Итак, искомые решения составляют множество { 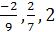 }
}
Метод интервалов
Метод интервалов используется при решении неравенств довольно общего вида: f(x) V g(x), где V — знак ≤, ≥, <, >. Единственным ограничением на функции f и g является требование их непрерывности. Отметим, что все элементарные функции непрерывны на своей области определения.
